Introduction

Nous avons vu au premier chapitre comment l'on pouvait faire de la logique propositionnelle de ma­niè­re calculatoire sans se préoccuper de l'interprétation de ces calculs, à la manière du calcul en ari­thmé­ti­que. Il ne reste plus qu'un pas à franchir pour achever cette métamorphose en calcul al­gé­bri­que, et c'est le mathématicien britannique George Boole qui l'a réalisée à l'aube du 20-ème siècle. Boole a noté des si­mi­li­tu­des entre le calcul algébrique sur les nombres comme l'addition et la multiplication, et le calcul en logique pro­po­si­tion­nelle avec la disjonction et la conjonction de valeurs de vérité et a fait le pont entre ces deux visions. Il a en quelque sorte algébrisé la logique.

Les applications de l'al­gè­bre qui porte aujourd'hui son nom sont innombrables et centrales en in­for­ma­ti­que, en automatique et en électronique. Les circuits qui constituent un ordinateur s'appuient sur des circuits logiques qui font exclusivement du calcul booléen à partir de portes logiques. C'est le mathématicien Claude Shannon qui a été l'un des premiers à appliquer l'algèbre de Boole à la conception des circuits. Les calculs réalisés par les circuits logiques sont la matérialisation des calculs abstraits réalisés en algèbre de Boole.

Certains concepts utilisés dans ce chapitre ne seront abordés que dans les chapitres suivants, comme les structures algébriques, les applications et les fonctions. Nous aurions donc pu différer l'étude de l'algèbre de Boole, mais ce chapitre est dans la continuité de l'étude de la logique propositionnelle, et ce que le lecteur connaît déjà de ces concepts est suffisant pour pouvoir les utiliser sans une étude préalable.

Algèbre de Boole

En logique propositionnelle nous avons étudié plusieurs opérateurs logique dont la négation, la dis­jonc­tion et la conjonction, notés res­pec­ti­ve­ment \(\neg a\), \(a\vee b\) et \(a\wedge b\). La conjonction et la disjonction logiques sont des lois de compositions internes*(*) Nous étudierons les lois de composition au chapitre prochain. sur l'ensemble \(\{vrai,\,faux\}\), c'est-à-dire que le résultat d'une conjonction ou d'une disjonction est toujours un élément de l'ensemble \(\{vrai,\,faux\}\). Nous avions interprété les symboles \(\top\) et \(\perp\) en vrai et faux respectivement, cette fois nous allons coder la valeur logique vrai (resp. faux) par le nombre entier 1 (resp. 0) et transposer la disjonction et la conjonction en addition et en multiplication.

On munit l'ensemble \(\B:=\{0,1\}\) d'une structure algébrique particulière appelée algèbre de Boole, comportant une opération additive, une opération multiplicative et la négation. Un élément de l'ensemble \(\B\) est donc un booléen. Les valeurs \(0\) et \(1\) sont souvent qualifiées de bits, contraction des deux mots américains binary et digits et parfois de logons^#. ^(#) unité de logique ou d'information en France. On traduit les tables de vérité des opérateurs logiques de disjonction et de conjonction res­pec­ti­ve­ment en tables d'addition et de mul­tip­li­ca­tion :

Pour simplifier l'écriture des expressions logiques, l'opérateur de négation \(\neg\) peut-être noté dif­fé­rem­ment lui aussi, et on écrit \(\overline{x}\) au lieu de \(\neg x\). Et on a

Dans le cadre de l'algèbre de Boole, un littéral désigne là aussi une variable \(x\) (littéral positif) ou sa négation \(\overline{x}\) (littéral négatif).

Les trois opérateurs fonctionnent de manière analogue à ce que leurs notations algébriques suggèrent en héritant essentiellement des mêmes propriétés que s'il s'agissait d'un calcul dans \(\Z\). La loi mul­ti­pli­ca­ti­ve est ainsi souvent notée \(\cdot\) et on omet parfois de l'écrire dans les ex­pres­sions al­gé­bri­ques quand il n'y aucune ambiguité, par exemple \(x(y+z)\) au lieu de \(x\cdot(y+z)\) ou \(x\times(y+z)\). On dispose d'autre part des nom­breu­ses propriétés suivantes héritées de celles du calcul propositionnel. On désigne ci-dessous par \(a\), \(b\) et \(c\) des variables booléennes quelconques*(*) Cette phrase est une manière informelle de quan­ti­fier les va­riab­les boo­lé­en­nes dans cha­cu­ne des \(12\) pro­po­si­tions. :

1. Associativité : \( (a+b)+c=a+(b+c)=a+b+c\ \ \text{et}\ \ (a\,b)\,c=a(b\,c)=a\,b\,c. \)
2. Commutativité : \( a+b=b+a\ \ \text{et}\ \ a\,b=b\,a. \)
3. Distributivité : \( a(b+c)=a\,b+a\,c\ \ \text{et}\ \ a+(b\,c)=(a+b)(a+c). \)
4. Idempotence : \( a+a+\cdots+a=a\ \ \text{et}\ \ a\,a\cdots a = a. \)
5. Élément neutre : \( a+0=0+a=a\ \ \text{et}\ \ a\,1=1\,a=a. \)
6. Absorption : \( 0\,a=0\ \ \text{et}\ \ 1+a=1. \)
7. Simplification : \( a+\overline{a}\,b=a+b\ \ \text{et}\ \ a(\overline{a}+b)=a\,b. \)
8. Redondance : \( a\,b+\overline{a}\,c=a\,b+\overline{a}\,c+b\,c \ \ \text{et}\ \ (a+b)(\overline{a}+c)=(a+b)(\overline{a}+c)(b+c). \)
9. De Morgan : \( \overline{a+b} = \overline{a}\;\overline{b}\ \ \text{et}\ \ \overline{a\;b} = \overline{a}+\overline{b}. \)
10. Involution : \( \bar{\bar{a}}=a. \)
11. Tiers-exclu : \( a+\overline{a}=1. \)
12. Non-contradiction : \( a\,\overline{a}=0. \)

Le principe de dualité permet de déduire les propriétés de l'addition des propriétés de la mul­ti­pli­ca­tion et réciproquement, il suffit d'échan­ger le rôle des opérateurs \(+\) et \(\times\) et celui des valeurs \(0\) et \(1\). Par exemple \(a\cdot 1=1\cdot a=a\) est la propriété duale de \(a+0=0+a=a\). Les lois de De Morgan sont deux lois duales, tout comme la règle du tiers-exclu et la non-contradiction.

On retrouve les cinq autres opérateurs binaires, d'implication, d'équi­va­len­ce, de dis­jonc­tion ex­clu­si­ve, de non conjonction et de non disjonction construits à partir des trois opérateurs de base et des identités sui­van­tes :

Et on en tire les tables de calcul suivantes (attention, ces opérateurs binaires ne sont pas tous commutatifs, par convention les valeurs de l'opérande gauche sont placées dans la colonne gauche, celles de l'opérande droit sur la ligne supérieure) :

La lecture de ces tables est instructive sans même faire de calcul à proprement parler. La négation des valeurs dans la table de calcul de l'équivalence fournit manifestement la table de calcul du ou exclusif, soit \begin{equation} \label{eq:oplusiff} \overline{a\iff b}= a\oplus b, \end{equation} ce que nous allons démontrer à l'aide du calcul booléen. D'après \((\ref{equiv:iff})\) et \((\ref{equiv:oplus})\) il nous faut vérifier que

Notons qu'il s'agit cette fois d'un égalité et plus d'une équivalence logique puisqu'on calcule dans l'en­sem­ble \(\{0,1\}\). Nous indiquons à droite la propriété qui est appliquée : \begin{align*} \overline{(\overline{a}+b)(a+\overline{b})}&= \overline{(\overline{a}+ b)} + \overline{(a+\overline{b})}&&\text{(De Morgan)}\\ &=(a\, \overline{b}) + (\overline{a}\,b)&&\text{(De Morgan)}\\ &=\big((a\, \overline{b}) + \overline{a}\big)\,\big((a\, \overline{b}) + b\big) &&\text{(distributivité)}\\ &=\big(({\color{#88F}a+\overline{a}}) \, (\overline{b}+\overline{a})\big)\,\big((a+ b)\,({\color{#88F}\overline{b}+ b})\big)&&\text{(distributivité)}\\ &=\big({\color{#88F}1}\, (\overline{b}+\overline{a})\big)\,\big((a+ b)\, {\color{#88F}1}\big)&&\text{(tiers exclu)}\\ &=(\overline{b}+\overline{a})\,(a+b)&&\text{(élément neutre)}\\ &=(a+b)\,(\overline{a}+\overline{b})&&\text{(Commutativité)} \end{align*}

L'algèbre de Boole se contente des opérateurs de négation, de conjonction et de disjonction puisqu'ils suffisent à décrire tous les opérateurs binaires possibles. L'exercice ci-dessous a pour objectif de montrer que l'on peut décrire tous les opérateurs unaire et binaires avec un unique opérateur, ce qui permet de construire des circuits logiques complexes avec un seul type de circuit de base.

Fonctions booléennes

Définition

Les fonctions booléennes sont utilisées non seulement dans la modélisation des circuits logiques mais également en théorie de la complexité, en théorie de l'information et en particulier en codage et en cryp­to­gra­phie.

Les fonctions logiques sont intimement liées aux interprétations des formules de la logique pro­po­si­tion­nel­le. Toute formule construite à partir de \(n\) variables pro­po­si­tion­nel­les se traduit par une fonc­tion logique \(f\) de \(n\) variables booléennes \((x_1,x_2,\ldots,x_n)\in\B^n\). À chaque interprétation des variables pro­po­si­tion­nel­le correspond une valeur de la fonction en le \(n\)-uplet correspondant. La table de vérité caractérise donc la fonction et réciproquement les différentes valeurs d'une fonction booléenne fournit la table de vérité de la formule cor­res­pon­dan­te de la lo­gi­que pro­po­si­tion­nel­le.

Considérons par exemple la formule \(P\wedge(Q\vee R)\). La fonction booléenne associée est définie par \begin{equation} \label{eq:foncbool} f(x_1,x_2,x_3):=x_1(x_2+x_3). \end{equation} en identifiant les variables propositionnelles \(P\), \(Q\) et \(R\) aux variables booléennes \(x_1\), \(x_2\) et \(x_3\) respectivement. L'interprétation \(I(P)=V\), \(I(Q)=F\) et \(I(R)=F\) est associée au triplet \((1,0,0)\). L'évaluation de cette fonction en les \(2^3=8\) valeurs possibles des triplets \((x_1,x_2,x_3)\) de \({\mathscr B}^3\) permet donc de construire la table de vérité de la formule \(P\wedge(Q\vee R)\).

C'est bien sûr une involution, \((f^*)^*=f\). La duale de la fonction constante égale à 1 est la fonction constante égale à 0. La duale de la fonction somme \(x+y\) est la fonction produit \(x\cdot y\) et la fonction duale du ou exclusif est l'équivalence logique. C'est une autre façon d'exprimer le principe de dualité.

Formes normales canoniques

De la même manière que deux formules de la logique propositionnelle peuvent être logiquement équivalentes sans pour autant avoir la même expression, on peut exprimer une même fonction de différentes manières, les propriétés du calcul booléen énumérées plus haut jouent précisément sur la variété des expressions d'une même fonction. Par exemple, les deux fonctions \(f(x,y):=x\,(x+y)\) et \(g(x,y):=x\,y+x\) sont égales, on peut s'en convaincre en calculant leurs images.

Parmi toutes les expressions possibles sous forme normale d'une même fonction booléenne \(f\), nous allons nous intéresser à deux formes particulières, appelées formes normales canoniques de \(f\). Considérons trois variables booléennes \(x\), \(y\) et \(z\) et les huit fonctions booléennes de \(\B^3\to\B\)

Pour chacune de ces 8 conjonctions, il n'existe qu'un seul triplet \((x,y,z)\) parmi les 8 triplets pos­si­bles dont l'image par la fonction vaut 1, les 7 autres valeurs sont nulles :

Par dualité, on étudie les 8 disjonctions obtenues par négation des 8 conjonctions de \((\ref{eq:min3})\) et cette fois l'image de la fonction n'est nulle qu'une seule fois sur les huit triplets possibles :

Cet exemple motive la définition suivante :

La preuve du deuxième corollaire fournit un algorithme pour trouver l'expression en mintermes ou en maxtermes d'une fonction booléenne, il suffit de collecter respectivement les \(n\)-uplets pour les­quels la fonction vaut 1 et 0 dans sa table de vérité.

On calcule tout d'abord la table de vérité de la fonction \(\color{#FF8}f\) :

Puis les deux formes normales canoniques de la fonction \(\color{#FF8}f\) :

L'algorithme naïf qui permet de déterminer les formes normales ca­no­ni­ques disjonctive et conjonctive d'une fonction booléenne est malheureusement fort peu efficace puisqu'il faut réa­li­ser un nombre expo­nen­tiel de calculs.

Circuits logiques

Portes logiques

Il ne reste plus beaucoup de chemin à parcourir pour passer des écritures abstraites des formules propositionnelles ou des fonctions booléennes à la réalité concrète des circuits électroniques. Sché­ma­ti­que­ment, on peut voir une fonction booléenne \(f\) de \(n\) variables comme une boite avec \(n\) entrées binaires et une sortie binaire. On cherche à réaliser physiquement cette boite noire, à l'aide d'un circuit électronique. Les \(n\) entrées et la sortie de la boite sont réalisées à l'aide de \(n+1\) fils électriques sous tension ou non, la tension re­pré­sen­tant la valeur 1 et l'absence de tension 0 (grossièrement).

Pour chaque opération logique, on peut fabriquer à l'aide de transistors un circuit électronique qui la réalise. Un tel circuit est appelé une porte logique. Nous en présentons ici six, ce sont les opérateurs de négation de conjonction et de disjonction, de non conjonction, de non-disjonction, de disjonction exclusive. Les portes correspondantes sont très souvent symbolisées par

NON	ET	NON ET	OU	NON OU	OU EXC.

Portes logiques associées à \(\neg\), \(\wedge\), \(\uparrow\), \(\vee\), \(\downarrow\) et \(\oplus\).

La ou les entrées sont à gauche et la sortie à droite de chaque circuit. On connecte les sorties aux en­trées des différents circuits pour réaliser une fonction booléenne. Considérons par exemple la fonction booléenne de trois variables

Dans un schéma bi-dimensionnel représentant un circuit logique, il est inévitable que les fils se croisent alors qu'ils ne se croisent pas en réalité dans l'espace 3D. Ainsi, par convention deux fils qui se croisent ne sont pas con­nec­tés électriquement. Dans le cas contraire, on le signifie par un disque plein sur la connexion (par exemple juste à côté de \(x\) dans le schéma ci-dessous). Une telle connexion entre trois fils est qualifiée de circuit duplicateur.

Circuit logique de \(f(x,y,z):=\bar{x}\,(y+\bar z)+\overline{xz}.\)

De nombreuses questions se posent aux électroniciens qui doivent concevoir ce type de circuit. Par exem­ple comment concevoir un circuit équivalent (au sens logique) qui utilise le moins possible de composants de base ? Comment dessiner un tel circuit afin d'éviter au maximum les croisements sur les pistes ? Peut-on déterminer facilement si un circuit est défectueux ? Comment tester les \(2^n\) entrées possibles d'un circuit à \(n\) entrées en ne changeant qu'un bit de l'entrée à chaque fois ?

Opérateurs bit à bit

On généralise aisément les différents opérateurs binaires définies sur l'ensemble \({\mathscr B}\) des booléens à l'en­semb­le \(\N\) des entiers naturels. On considère pour cela l'écriture binaire \(b_{n-1}b_{n-2}\ldots b_2b_1b_0\) d'un entier \(x\) sur \(n\) chiffres (bits), c'est-à-dire : \begin{equation} x=\sum_{i=0}^{n-1}b_i2^i. \end{equation} Le chiffre \(b_{n-1}\) à gauche (resp. \(b_0\) à droite) est appelé bit de poids fort (resp. bit de poids faible) de \(x\).

On applique alors l'opérateur binaire à chacun des \(n\) chiffres de la dé­com­po­si­tion bi­nai­re des deux opérandes entiers. Par exemple \(20 + 13=29\). En effet : \begin{align*} &\ 1\,0\,1\,0\,0 &&(=20)\\ + &\ 0\,1\,1\,0\,1 &&(=13)\\ =&\ 1\,1\,1\,0\,1 &&(=29) \end{align*}

On dispose aussi de deux opérateurs très utiles qui permettent de décaler les chiffres binaires d'un nombre \(x\) vers la droite ou vers la gauche de \(s\) positions notés respectivement \(x\gg s\) et \(x\ll s\) et appelés décalages. Dans le premier cas \(x\gg s\), les \(s\) bits de poids fort de \(x\) sont remplacés par des \(0\) et les \(s\) bits de poids faible sont perdus et réciproquement pour un décalage à gauche \(x\ll s\). Par exemple \(25\gg 2=6\) et \(7\ll 3 =56\).

Codes de Gray

On va s'intéresser à présent à l'énumération des \(2^n\) valeurs lo­gi­ques possibles de \(n\) variables boo­léen­nes. Généralement quand on veut décrire l'ensemble des valeurs binaires possibles de \(n\) variables, on utilise la représentation binaire des entiers de \(0\) à \(2^n-1\) et on passe d'un entier à l'entier suivant en additionnant 1. Pour \(n=3\) cela donne la sé­quen­ce :

Cette façon d'énumérer peut poser des problèmes physiques, par exemple dans l'utilisation de comp­teurs numériques. Quand un compteur doit passer d'une valeur à la suivante et que plusieurs bits sont modifiés, tout problème de synchronisation peut faire que ces bits ne basculent pas tout à fait si­mul­ta­né­ment, créant ainsi des valeurs intermédiaires très différentes de la valeur courante et de la suivante. Par exemple en passant de l'entier \(3\) à \(4\), c'est-à-dire de la séquence \(0\,{\color{orange}1}\,1\) à la séquence \(1\,0\,0\), si le deuxième bit est le premier à basculer, on aurait la séquence \(0\,0\,1\) soit la valeur \(1\) temporairement.

D'autre part, un chan­ge­ment d'état sur le \(k\)-ème bit se fait électriquement et provoque une usure de la bascule et on observe qu'avec l'énumération classique des \(n\) valeurs logiques ci-dessus, l'usure des \(n\) circuits n'est pas homogène. La durée de vie des disques de type ssd est fixée par le nombre de bascules des cellules mémoire et il est crucial qu'il n'y ait pas de déséquilibre pour éviter une usure prématurée. Observons combien de fois chaque bit à été modifié en supposant que l'on boucle sur le premier code. Le bit de poids faible (le chiffre le moins si­gni­fi­ca­tif à droite) a été modifié 8 fois, le bit suivant 4 fois et le bit de poids fort (le chiffre le plus si­gni­fi­ca­tif à gauche) 2 fois.

Un premier code de Gray*(*) Frank Gray était un physicien américain qui travaillait aux Bell Labs. fournit une solution au problème de synchronisation. La table ci-dessous fournit les \(8\) codes de Gray des entiers de \(0\) à \(7\). On peut constater qu'il s'agit d'une permutation de leurs écritures binaires et que l'on passe du code d'un entier au code de l'entier suivant en ne changeant qu'un seul bit. Ce premier code va permettre de résoudre le problème de la synchronisation et nous l'illustrerons plus loin avec le codage des directions fournies par une boussole.

En utilisant le décalage circulaire, le code de Gray d'un entier \(x\) est donc égal à \(x\oplus (x \gg 1)\). Par exemple le code de Gray de l'entier \(13\) dont la représentation est \(1101\) en base \(2\) s'obtient avec

À partir du code de Gray d'un entier, on obtient le code de Gray du suivant en appliquant cette règle : si le poids du code de Gray est impair alors on inverse le bit à gauche du bit de poids faible (le 1 le plus à droite), sinon on inverse le bit le plus à droite. Cette procédure permet de construire le code de Gray en dimension \(n\) en partant de 0 et en répétant \(2^n-1\) fois cette règle.

Un disque est constitué de 4 anneaux concentriques. Ce disque est découpé à la manière d'une orange en \(16\) portions de \(4\) segments coloriés en noir et blanc selon la figure ci-dessous :

Schéma d'un encodeur rotatif optique.

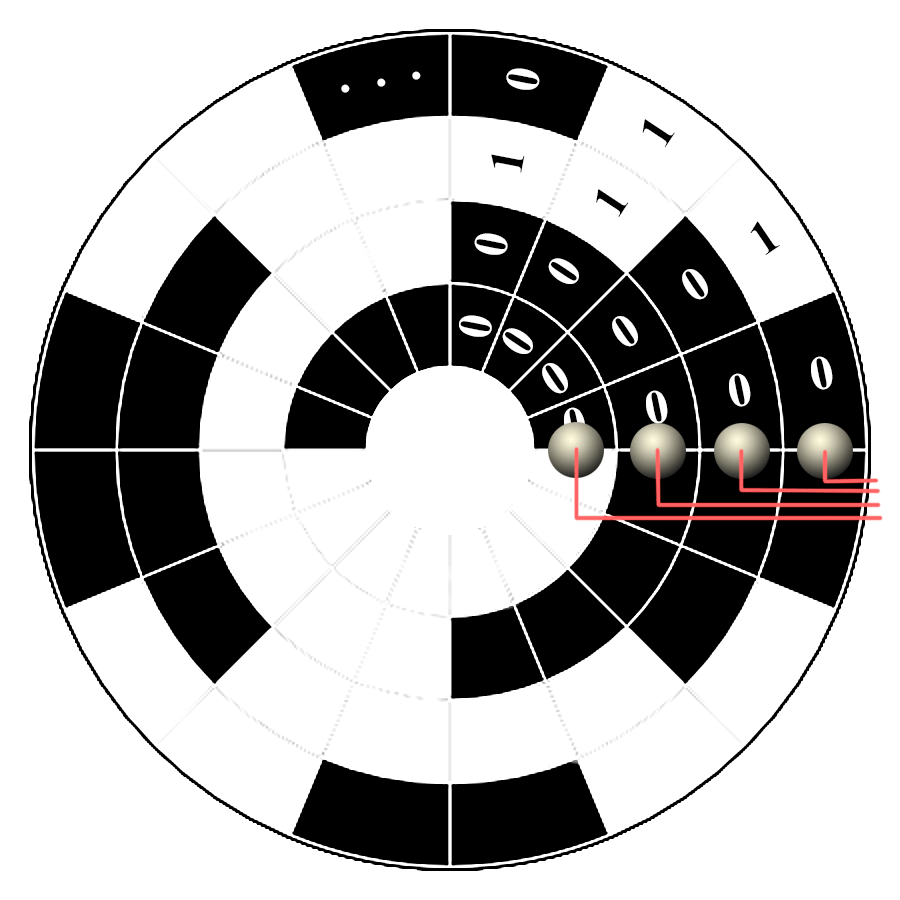
Ce disque est en rotation autour de son axe et quatre cellules optiques fixes sont placées à intervalle régulier sur un quartier du disque de manière à mesurer la lumière réfléchie par chaque portion des 4 anneaux. Quand la portion est blanche, la lumière réfléchie crée un courant électrique qui est interprété comme 1. Quand la portion est noire, le courant induit est nul ou très faible et interprété comme 0. Ce dispositif permet donc de coder 16 directions différentes avec uniquement \(4\) cellules. Mais pourquoi un code de Gray de dimension 4 plutôt qu'un codage binaire ?

L'avantage d'un code de Gray par rapport au code binaire est déterminant. Il y a évidemment une tolérance sur l'alignement des cellules et le partitionnement du disque. Imaginons une légère oscillation du disque tel que les 4 cellules hésitent entre deux quartiers adjacents. Avec un code de Gray, une seule cellule peut changer de valeur, ces oscillations vont se traduire par le code de deux directions adjacentes et proches de la réalité, alors qu'avec un code binaire classique, il est tout à fait possible que certaines cellules soient au-dessus d'un quartier et les autres au-dessus d'un autre quartier indiquant alors deux directions qui, non seulement ne sont pas adjacentes, mais qui peuvent également être très différentes de la réalité. Notons que si l'on veut plus de précision, il suffit d'augmenter la dimension du code de Gray.

Encodeur rotatif d'un code de Gray (ani­ma­tion de Perlygatekeeper licence CC.)

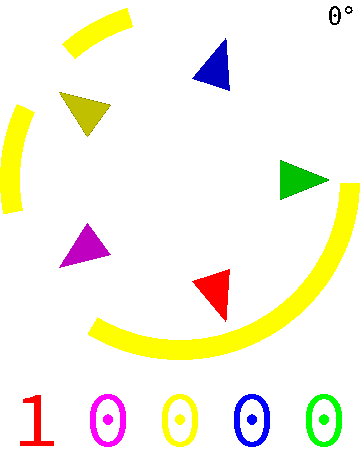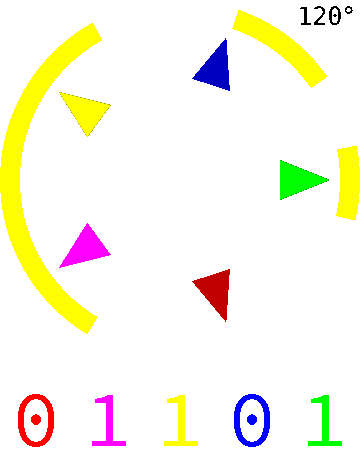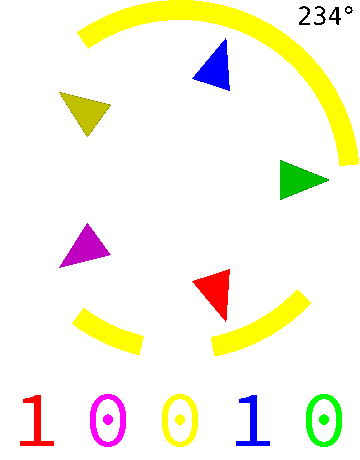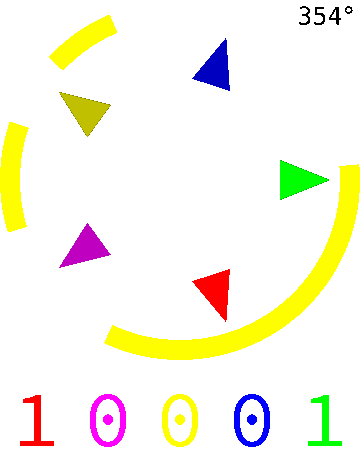
Pour obtenir une boussole avec une précision de l'ordre du degré, il suffit d'un jeu de 9 cellules (\(2^9=512>360\)). On peut réaliser un tel disque avec un mécanisme moins évolué que des cellules optiques, par exemple à l'aide de simples contacteurs en creusant une gorge sous les anneaux dans les portions noires (ou réciproquement selon le type de contacteurs). On peut également placer des contacteurs à l'intérieur d'un cylindre conducteur rotatif sur lequel on a découpé des fenêtres pour arrêter la conduction. Dans l'animation, les \(5\) bits permettent de coder \(2^5=32\) angles différents, les contacteurs étant de la même couleur que le bit associé dont la valeur change en fonction de la position des fenêtres du cylindre.

Un autre code de Gray permet de répondre au problème d'homogénéité des changements, à savoir le nombre de changements d'état des \(n\) bits lors d'une énumération. On voudrait que le nombre de changements d'états soit le même pour chacun des \(n\) bits, ou à défaut le plus équilibré possible. Cela permet, par exemple, de tester les entrées d'un circuit logique de manière équitable. L'existence et la construction de tels codes est récente et n'est pas triviale. En voici un pour \(n=4\) présenté en colonnes cette fois pour plus de lisibilité. Dans ce code, il y a exactement \(4\) modifications pour chacun des \(4\) bits (ils sont distingués en jaune avant le changement) :

Pour conclure, on peut se demander si l'on peut également minimiser le nombre de changements en plus de l'équilibre.

Tables de Karnaugh

Nous allons nous intéresser au problème de la simplification des circuits. Afin d’utiliser un nombre minimum de portes logiques pour réaliser une fonction booléenne \(f\), il faut qu’elle comporte le moins de variables et le moins d’opérateurs possibles. Le travail se fait en amont du circuit en cherchant une décomposition de \(f\) la plus simple possible. Pour cela on utilise les tables de Karnaugh*(*) Maurice Karnaugh est un mathémati­cien amé­ricain qui a dé­ve­lop­pé cette tech­ni­que en 1954 aux Bell Labs.. Les tables de Karnaugh sont une autre façon de représenter une table de vérité, elles permettent plus facilement de visualiser la forme d'une fonction mais ne sont efficaces que pour un nombre très restreint de variables, pas plus de quatre généralement. Elles ne sont utilisées que pour résoudre des problèmes de conception de circuit à la main.

Les tables de Karnaugh vont nous permettre :

1. de trouver la forme normale conjonctive et la forme normale disjonctive d’une fonction booléenne,
2. de trouver une expression simplifiée de la fonction booléenne avec le minimum de variables et d’opérateurs.

Les variables sont partitionnées en deux groupes de même taille. Si le nombre de variables est impair, un groupe en contient une de plus. Les différentes valeurs possibles des variables du premier groupe indexent les lignes de la table, celles du second groupe les colonnes de la table. Seule la valeur \(1\) de la fonction est notée dans la table. Considérons par exemple les trois fonctions boo­léen­nes de 2, 3 et 4 variables suivantes :

1. \(\phantom{,z,t}f(x,y) := {\color{#FF8}x}\,(\bar{\color{#FF8}x}+y)+\bar{\color{#FF8} x}\),
2. \(\phantom{,t}g(x,y,z) := {\color{#FF8}x}\,{\color{#88F}y}+\bar z\),
3. \(h(x,y,z,t) := {\color{#FF8}x}\,{\color{#F44}y}+\bar {\color{#88F}z}(\bar {\color{#FF8}x}+{\color{#F44}y}+t)\).

Les tables de Karnaugh de ces trois fonctions booléennes sont :

La méthode pour retrouver la forme normale disjonctive ou conjonctive canonique est la même que pour les tables de vérités, il suffit de lire les 1 ou les cases vides et de rajouter le minterme ou le maxterme correspondant. Ainsi pour la fonction de trois variables de l'exemple ci-dessus, on ob­tient la forme normale dis­jonc­ti­ve canonique :

Ce n'est pas tant pour trouver les formes canoniques que l'on utilise les tables de Karnaugh, on ne gagne rien par rapport à la table de vérité usuelle, mais plutôt pour simplifier rapidement les expressions des fonctions booléennes. La base de la simplification repose sur l'iden­ti­té suivante, où \(a\) est une variable et \(e\) une expression booléenne :

En effet, \(ea+e\overline{a}=e(a+\overline{a})=e.1=a\). Cette identité est exploitée en rangeant les différentes valeurs possibles des variables logiques sui­vant un code de Gray. Ceci assure qu'entre deux cases adjacentes — y compris la dernière avec la pre­miè­re sur la même ligne ou la même colonne — il n'y a qu'une variable booléenne qui change de valeur. De cette manière, si deux cases adjacentes contiennent la valeur \(1\), on peut éliminer la variable qui a changé de valeur puisque la somme des deux mintermes correspondants est de la forme \((\ref{eq:suminterms})\). Pour la fonction \(g\) dont l'expression a été obtenue en \((\ref{eq:fonctiong})\), on peut par exemple éliminer la variable \(\color{#88F}y\) puisque la première et la dernière case de la première ligne contiennent \(1\) et c'est la valeur de \(y\) qui change entre les deux.

Reprenons la fonction \(f(x,y)=x\,(\bar x+y)+\bar x\). Sa table de Karnaugh et sa forme normale dis­jonc­ti­ve canonique sont

On observe deux regroupements possibles dans cette table, les deux cases sur la première ligne ou les deux cases sur la dernière colonne :

On peut donc écrire \(f(x,y)=\overline{x}+xy\) ou encore \(f(x,y)=\overline{x}\,\overline{y}+y\) et la propriété de simplification nous donne finalement \(f(x,y)=\overline{x}+y\).

Travaux pratiques

L'objectif de ces travaux pratiques est de réaliser un script Python qui calcule la table de vérité puis les formes nor­ma­les canoniques conjonctives et disjonctives d'une fonction booléenne donnée en paramètre. Il s'agit principalement de traduire l'expression d'une fonction booléenne en une formule de la logique propositionnelle dont la syntaxe est celle du langage Python.

Nous saisirons les expressions algébriques des fonctions booléennes à l'aide du lexique suivant :

• les lettres (en minuscule) de \(\color{#FF8}a\) à \(\color{#FF8}z\) pour décrire les variables booléennes,
• les parenthèses \(\color{#FF8}(\) et \(\color{#FF8})\),
• les symboles \(\color{#FF8}!\), \(\color{#FF8}+\) et \(\color{#FF8}*\) codant respectivement la négation, la disjonction (ou) et la conjonction (et).

Par exemple, la chaîne de caractères

On décompose le travail en écrivant plusieurs fonc­tions. Une fois ce travail achevé, vous pourrez compléter votre script TP1.py pour l'exécuter dans un terminal et obtenir, une fois la chaîne !(p + q) * (!p + r) + (p * q) saisie pour définir la fonction booléenne :

En séance

Compléments hors séance