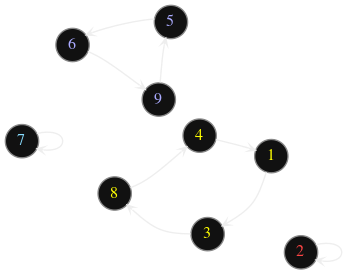
Le but du jeu est de ranger les 15 pièces dans l'ordre croissant de \(1\) à \(15\) en faisant coulisser les pièces le long des lignes et des colonnes. Sam Loyd proposa la somme de $1.000 au premier qui trouverait une solution. Vous pouvez essayer vous-même avec le simulateur ci-dessus qui vous permet de faire glisser jusqu'à trois pièces alignées vers la case vide d'un seul coup plutôt que les déplacer les unes après les autres.
Ce jeu a été décliné de très nombreuses façons, par exemple en remplaçant les nombres par des portions d'une image à reconstituer à la manière d'un puzzle. Le célèbre Rubik's Cube est en quelque sorte une extension à trois dimensions de ce problème. L'objectif de ce chapitre est de comprendre pourquoi Sam Loyd ne risquait pas de perdre ses $1.000 et de trouver comment résoudre d'autres configurations, quand elles admettent une solution.Nous avons étudié aux chapitres précédents, les ensembles puis les relations qui pouvaient les lier et leur cardinalité. Nous allons à présent les animer en les équipant de quelques rouages.
Il s'agit d'observer le fonctionnement des opérations bien connues sur les nombres (addition, multiplication, etc.) et de les généraliser à des ensembles quelconques. On cherche donc à déterminer les propriétés qu'elles partagent plutôt que leurs particularités, et d'en tirer des résultats universels susceptibles d'être appliqués à toutes sortes de situations.
Que ce soit l'addition et la multiplication définies sur les entiers naturels ou encore la réunion et l'intersection définies sur les parties d'un ensemble, ces opérations ont pour premier point commun de composer deux éléments d'un ensemble de référence pour obtenir un élément de ce même ensemble :
Pour exprimer la composition de deux éléments \(x\) et \(y\) de \(X\), on préfére généralement la notation infixe \(x\;{\color{#FF8}\diamond}\;y\) à la notation préfixe \({\color{#88F}\,\diamond}\,(x,y)\) des applications. La notation postfixe \((x,y)\,{\color{#8F8}\diamond}\), assez peu usitée dans les écritures mathématiques, s'avèrera particulièrement adaptée pour réaliser des calculs effectifs.
Dans tout le chapitre, \((X,\diamond)\) désignera un magma.
Exemples. L'addition et la multiplication définies sur l'ensemble des entiers naturels \(\N\) au chapitre Combinatoire sont donc des lois de composition internes faisant de \((\N,+)\) et \((\N,\times)\) deux magmas. La réunion \(\cup\) et l'intersection \(\cap\) sur \({\mathscr P}(X)\) l'ensemble des parties d'un ensemble \(X\) sont des lois de composition internes faisant de \(({\mathscr P}(X),\cup)\) et \(({\mathscr P}(X),\cap)\) deux magmas. La composition des applications \(\circ\) d'un ensemble \(X\) dans lui-même, définit une loi de composition interne sur \(X^X\) faisant de \((X^X,\circ)\) un magma. La concaténation \(\cdot\) est une loi de composition interne sur l'ensemble \(\Sigma^*\) des mots définis sur un alphabet fini \(\Sigma\) faisant de \((\Sigma^+,\cdot)\) un magma.
Une partie \(A\) de \(X\) est dite stable pour la loi \(\diamond\) si et seulement si tous les composés d'éléments de \(A\) sont eux aussi des éléments de \(A\) : \begin{equation} \forall (x,y)\in A \times A\quad x\diamond y \in A. \end{equation}
Dans ce cas, la restriction de la loi de composition \(\diamond\) aux éléments de \(A\times A\) est une loi de composition interne sur \(A\), appelée loi induite par \(\diamond\) sur \(A\), et on conserve la même notation pour le magma \((A,\diamond)\).
Exemples. L'ensemble \(2\,\N\) des entiers pairs est une partie stable pour la loi d'addition \(+\) sur l'ensemble des entiers naturels \(\N\) faisant de \((2\,\N,+)\) un magma. L'ensemble \(S(X)\) des bijections d'un ensemble \(X\) sur lui-même est une partie stable de \(X^X\) pour la loi de composition des applications \(\circ\).
Une loi de composition interne \(\diamond\) est dite associative si et seulement si \begin{equation} \forall (x,y,z)\in X^\quad x\diamond(y\diamond z)= (x\diamond y)\diamond z. \end{equation} Dans ce cas le magma est dit associatif.
Exemples. L'addition et de la multiplication sur les entiers naturels sont deux lois associatives, c'est cette propriété qui nous permet de nous affranchir des parenthèses dans l'expression \(x+y+z\) et l'expression \(x\times y\times z\). Ces expressions n'auraient pas de sens si ces lois n'étaient pas associatives. Le magma \((X^X,\circ)\) est associatif (cf. exercice). La loi puissance est bien une loi de composition interne sur \(\N\), mais n'est pas associative, par exemple \(2^{(2^3)}=256\) alors que \((2^2)^3=64\).
On dit que deux éléments \(x\) et \(y\) de \(X\) commutent si et seulement si \begin{equation} x\diamond y = y \diamond x. \end{equation}
On appelle centre d'un magma, le sous-ensemble \(Z_X\) des éléments de \(X\) qui commutent avec n'importe quel élément de \(X\) : \begin{equation} Z_X:=\{z\in X\such\forall x\in X\ \ z\diamond x=x\diamond z\}. \end{equation} Si \(Z_X=X\), le magma est dit commutatif.
Exemples. Le magma \((\N,+)\) est commutatif, tout comme \((\R,\times)\). En revanche la loi de composition des applications \(\circ\) n'est pas commutative en général pour le magma \((X^X,\circ),\) on peut s'en convaincre en composant les applications \(n\mapsto n+1\) et \(n\mapsto 2n\) de \(\N^\N.\)
On appelle élément neutre pour la loi \(\diamond\) tout élément \(e\in X\) tel que \begin{equation} \label{eq:egelemneutre} \forall x\in X\quad x\diamond e = e \diamond x=x. \end{equation}
S'il existe un élément neutre, celui-ci est nécessairement unique. Un magma dont la loi possède un élément neutre est dit unifère.
Exemples. L'entier naturel \(0\) est l'élément neutre pour l'addition dans \(\N\) et l'entier \(1\) est l'élément neutre pour la multiplication dans \(\R\). L'ensemble \(X\) est l'élément neutre pour l'intersection sur l'ensemble \({\mathscr P}(X)\) des parties de \(X\). Le magma \((X^X,\circ)\) est unifère d'élément neutre l'application identique \({\Id}_X\).
Si un ensemble \(X\) est muni de deux lois de composition internes \(\star\) et \(\diamond\), on dit que \(\star\) est distributive à gauche (resp. distributive à droite) sur \(\diamond\) si et seulement si \begin{align} \forall (x,y,z)\in X^3\ \ x\star(y\diamond z) &= (x\star y)\diamond(x\star z),\\ \text{resp.}\ \ \forall (x,y,z)\in X^3\ \ (x\diamond y)\star z &= (x\star z)\diamond(y\star z). \end{align}
Si la loi est à la fois distributive à gauche et à droite, on dit simplement qu'elle est distributive. La multiplication \(\times\) est distributive sur l'addition \(+\) dans \(\N.\) \[\forall (a,b,c)\in\N^3\quad a\times(b+c)=(a\times b)+(a\times c).\]
Exemples. L'intersection \(\cap\) est distributive par rapport à la réunion \(\cup\) sur l'ensemble \({\mathscr P}(X)\) des parties d'un ensemble \(X\) et réciproquement : \begin{align*} \forall (A,B,C)\in{\mathscr P}(X)^3\quad A\cap(B\cup C)&=(A\cap B)\cup(A\cap C),\\ \forall (A,B,C)\in{\mathscr P}(X)^3\quad A\cup(B\cap C)&=(A\cup B)\cap(A\cup C). \end{align*}
Quand on doit résoudre une équation sur un magma \((X,\diamond)\), il est parfois possible de la simplifier si elle contient un élément particulier : on appelle élément régulier à gauche (resp. élément régulier à droite) tout élément \(r\in X\) tel que \begin{align*} \forall (x,y)\in X\times X\quad \underbrace{r\diamond x=r\diamond y}_{équation}\ \Rightarrow\ x=y\quad (\text{resp.}\ \ x\diamond r&=y\diamond r\ \Rightarrow\ x=y), \end{align*}
ce qui exprime que l'on est en mesure de simplifier l'équation à gauche et/ou à droite par un élément régulier à gauche et/ou à droite.
Un élément qui est la fois régulier à gauche et à droite est dit régulier.
Exemples. L'élément neutre pour une loi de composition interne quelconque est nécessairement régulier. Dans \(\N\), tout élément est régulier pour l'addition et tout élément non-nul est régulier pour la multiplication. Dans \({\mathscr P}(X)\) le seul élément régulier pour l'intersection est l'élément neutre \(X\).
Dans le même esprit et avec un outillage un peu plus évolué, il est possible de simplifier des équations plus facilement qu'avec des éléments réguliers. Soit \((X,\diamond)\) un magma unifère d'élément neutre \(e.\) On dit que \(x\in X\) est symétrisable à gauche (resp. symétrisable à droite) s'il existe (au moins) un élément \(x'\in X\) tel que \begin{align*} x'\diamond x=e\quad (\text{resp.}\ \ x\diamond x'&=e) \end{align*} On dit alors que \(x'\) est un symétrique à gauche (resp. symétrique à droite) de \(x\). On dit que \(x\) est symétrisable s'il est à la fois symétrisable à gauche et à droite.
On rencontre très fréquemment la structure suivante en informatique et en mathématiques :
D'autres combinaisons des propriétés que nous avons présentées sont récurrentes. Un magma associatif est appelé un semi-groupe. Un monoïde dont tous les éléments sont symétrisables est appelé un groupe et nous y reviendrons longuement plus loin tant cette structure est importante.
1. Soit \((s,t)\in X^2\) tels que \(x\diamond s=x\diamond t\) et \(x'\) un symétrique à gauche de \(x\), alors \begin{align*} x'\diamond(x\diamond s)&=x'\diamond (x\diamond t)\\ (x'\diamond x)\diamond s&=(x'\diamond x)\diamond t&\ &\text{car \(\diamond\) est associative}\\ e\diamond s&=e\diamond t&\ &\text{car \(x'\) symétrique à gauche de \(x\)}.\\ s&=t&\ &\text{car \(e\) est l'élément neutre pour \(\diamond\)}.\\ \end{align*} donc \(x\) est bien régulier à gauche. Un argumentaire symétrique permet de prouver la régularité à droite.
2. Notons \(x'\) un symétrique à gauche et \(x''\) un symétrique à droite de \(x\). Par définition, on a \begin{equation} \label{eq:proofpropsym} {\color{#FF8}(x'\diamond x)} = {\color{#88F}(x\diamond x'')} = e. \end{equation} Donc \begin{align*} {\color{#FF8}(x'\diamond x)}&=e\\ {\color{#FF8}(x'\diamond x)}\diamond x''&=e\diamond x''\quad\text{on compose à droite par \(x''\)}\\ x'\diamond{\color{#88F}(x\diamond x'')}&=x''\quad\text{associativité et \(e\) est neutre}\\ x'\diamond e&= x''\quad \text{d'après \((\ref{eq:proofpropsym})\)}\\ x'&= x''\quad\text{car \(e\) est neutre} \end{align*}
3. Soit \(x_1\) et \(x_2\) deux éléments de \(X\) de symétriques respectifs \(x_1'\) et \(x_2'\), uniques d'après 2. Alors \begin{align*} (x_1\diamond x_2)\diamond(x_2'\diamond x_1') &=(x_1\diamond (x_2 \diamond x_2'))\diamond x_1'&\ &\text{associativité}\\ &=(x_1\diamond e)\diamond x_1'&\ &\text{\(x_2'\) symétrique de \(x_2\)}\\ &=x_1 \diamond x_1'&\ &\text{\(e\) est neutre}\\ &=e&\ &\text{\(x_1'\) symétrique de \(x_1\)} \end{align*} On procède de la même manière pour montrer que \[ (x_2'\diamond x_1')\diamond(x_1\diamond x_2)=e. \] Ce qui prouve que \(x_1\diamond x_2\) admet \(x_2'\diamond x_1'\) pour symétrique.
Ces propriétés justifient que l'on emploie le singulier défini dans le symétrique d'un élément symétrisable.
L'entier naturel 0 est le seul élément qui admet un symétrique (lui-même) pour l'addition dans \(\N\), et \(1\) est le seul élément qui admet un symétrique (lui-même à nouveau) pour la multiplication dans \(\N\). L'ensemble des entiers relatifs \(\Z\) contient par construction, en sus des entiers naturels, tous leurs symétriques pour l'addition. En revanche pour la multiplication, seuls deux éléments de \(\Z\) admettent un symétrique, ce sont \(-1\) et \(1\). Les éléments symétrisables à gauche (resp. à droite) du magma \((X^X,\circ)\) sont les injections (resp. surjections). Les éléments symétrisables du magma \((X^X,\circ)\) pour la loi de composition des applications \(\circ\) sont donc les bijections.
Résoudre une équation consiste principalement à isoler l'inconnue en éliminant des termes de l'équation par simplification. Pour ce faire, il faut a minima que ces termes soient réguliers. S'ils sont symétrisables, les manipulations algébriques sont plus simples.
Soit \((X,\diamond)\) un monoïde et \(a\) et \(b\) deux éléments de \(X\). Considérons l'équation
\begin{equation} \label{eq:eqmonoide} a\diamond x=b \end{equation}Si \(a\) admet un symétrique à gauche \(a'\), alors il existe une unique solution. En effet en composant \(a'\) aux membres gauches et droits de l'identité \((\ref{eq:eqmonoide})\), on a :
\begin{align*} a'\diamond(a\diamond x)&=a'\diamond b\\ (a'\diamond a)\diamond x&=a'\diamond b\quad\text{par associativité},\\ e\diamond x&=a'\diamond b\quad\text{par symétrique à gauche},\\ x&={\color{#88F}a'\diamond b}\quad\text{car \(e\) est l'élément neutre}. \end{align*}Si \(a\) admet un symétrique à droite \(a''\), alors \(x={\color{#FC0}a''\diamond b}\) est une solution, en effet
\begin{align*} a\diamond({\color{#FF8}a''\diamond b})&=(a\diamond a'')\diamond b\quad\text{par associativité},\\ &=e\diamond b\quad\text{par symétrique à droite},\\ &=b\quad\text{car \(e\) est l'élément neutre}. \end{align*}D'après la proposition précédente, on sait que si \(a\) est symétrisable, \(a'=a''\) et dans ce cas \(a'\diamond b\) est l'unique solution de l'équation \((\ref{eq:eqmonoide}).\) L'étude est symétrique pour l'équation \(x\diamond a=b\) pour laquelle \(b\diamond a'\) est l'unique solution.
grep -E '^(0|1)*0[0|1]{2}$' fichier.txt
Cette commande unix cherche toutes les lignes du fichier fichier.txt qui ne sont composées que des symboles binaires \(0\) et \(1\) et qui se terminent par une séquence de trois bits dont le premier est un \(0\). Lorsque vous tapez cette commande grep, vous naviguez dans un monoïde, vous appliquez des lois de composition internes associatives, et vous bénéficiez d’algorithmes linéaires qui existent parce que ces structures sont bien définies.
De la même manière que pour une loi de composition interne, on dit qu'une partie \(A\) d'un ensemble \(X\) muni d'une loi de composition externe \(\star\) est stable pour cette loi si et seulement si \begin{equation} \forall(\alpha,x)\in\Omega\times A\quad \alpha\star x\in A. \end{equation}
Dans ce cas, en restreignant la loi aux éléments de \(A\), il s'agit encore d'une loi externe, appelée loi induite par \(\star\) sur \(A\).
Si l'on dispose d'un monoïde \((X,\diamond)\) d'élément neutre \(e\), on peut par exemple construire une loi de composition externe \(\cdot\) sur \(X\) à domaine d'opérateur \(\N\) en itérant la loi interne : c'est l'application puissance \(\N\times X\rightarrow X\) définie par \begin{equation} (n,x)\mapsto n\cdot x:=\begin{cases} e&\text{si}\ n=0,\\ \overbrace{x\diamond x\diamond\cdots\diamond x}^{n\ \text{fois}\ x}&\text{si}\ n > 0. \end{cases} \end{equation}
Quand la loi interne \(\diamond\) est notée comme une loi multiplicative, on utilise souvent l'écriture exponentielle \(x^n\) plutôt que \(n\cdot x\) pour désigner l'élément \(x\diamond x\diamond\cdots\diamond x\) et on en déduit immédiatement que \begin{equation} \label{eq:additivitéexp} x^n\diamond x^m=x^{n+m}. \end{equation}
Nous étudierons d'autres lois de composition externes dans les prochains chapitres.
Une relation binaire, une loi de composition interne ou externe sur un ensemble \(X\), définissent une structure sur cet ensemble.
Si deux ensembles \(X\) et \(Y\) sont chacun munis d'une structure de même nature (relation binaire ou loi de composition), il est naturel de s'intéresser aux applications \(f:X\rightarrow Y\) qui ne perturbent pas les structures respectives sur ces deux ensembles. S'il s'agit de relations binaires, les images de deux éléments en relation doivent rester en relation et s'il s'agit de lois de compositions, l'image de la composition de deux éléments doit être la composition de leurs images :
Exemples. Une application croissante est un morphisme d'ensembles ordonnés.
La notation exponentielle introduite en \((\ref{eq:additivitéexp}\)) définit un morphisme \begin{align*} p_x:(\N,+)&\longrightarrow(X,\diamond)\\ n&\longmapsto x^n \end{align*} puisque \(p_x(n+m)=x^{n+m}=x^n\diamond x^m=p_x(n)\diamond p_x(m)\).
La fonction exponentielle étudiée dans le cours d'analyse est également un morphisme de \((\R,+)\) dans \((\R,\times)\), en effet \(\text{exp}(x+y)=\text{exp}(x)\cdot\text{exp}(y)\).
La fonction définie par \(\theta\mapsto e^{i\theta}\) est un morphisme de \((\R,+)\) dans le cercle unité \(({\mathbb U},\cdot)\) muni de la multiplication complexe : \(e^{i(\theta+\theta')}=e^{i\theta}\cdot e^{i\theta'}\).
Si \(f:X\rightarrow Y\) est un morphisme injectif, on dit que c'est monomorphisme, s'il est surjectif on dit que c'est un épimorphisme. Si \(Y=X\), on dit que \(f\) est un endomorphisme. Si \(f\) est bijective et que la bijection réciproque \(f^{-1}\) est encore un morphisme on dit que \(f\) est un isomorphisme. Un isomorphisme de \(X\) dans lui-même est appelé un automorphisme. On précise souvent la nature du morphisme, c'est-à-dire la structure qui équipe les ensembles reliés par le morphisme, on parlera donc de morphisme d'ensembles ordonnés, ou de morphisme de semi-groupes ou de morphismes de groupes, etc.
L'égalité est une relation d'ordre sur tout ensemble \(X\), on considère donc \((X,=)\) et \((Y,\leq)\) où \(\leq\) désigne une relation d'ordre sur \(Y\). Si \(f:X\rightarrow Y\) est une application bijective et croissante, on a \(x=y\Rightarrow f(x)\leqslant f(y)\) mais pas toujours \(f^{-1}(x)\leqslant f^{-1}(y)\Rightarrow x=y\), prendre par exemple l'application de \(\Z^\Z\) définie par \(n\mapsto n+1\).
Soit \(X\) un ensemble muni d'une structure et \(Y\) un ensemble quelconque. Quand on dispose d'une bijection \(f:X\rightarrow Y\), on transporte facilement la structure de \(X\) à \(Y.\) Par exemple si \(\Rel{R}{X}\) est une relation binaire définie sur \(X\), il suffit de définir la relation \(\Rel{R}{Y}\) sur \(Y\) par \[ y\;\Rel{R}{Y}\;y'\Leftrightarrow f^{-1}(y)\;\Rel{R}{X}\;f^{-1}(y'). \]
Si plusieurs structures équipent un même ensemble, il est naturel de s'intéresser à leur cohabitation. L'omniprésence des relations d'équivalence et des lois de composition sur les ensembles justifie que l'on se questionne sur l'articulation d'une relation d'équivalence avec une loi de composition interne \(\diamond\) d'un magma \((X,\diamond)\).
Si l'on dispose d'une relation d'équivalence \(\rel\) et d'une loi de composition interne \(\diamond\) sur un ensemble \(X,\) on souhaite pouvoir équiper l'ensemble quotient \(X/\rel\) d'une loi de composition \(\overline{\diamond}\) héritée de \(\diamond\). Plus précisément, si \(A\) et \(B\) désignent deux classes d'équivalence pour \(\rel\), on veut définir la composition \(A\overline{\diamond} B\) comme la classe d'équivalence de \(a\diamond b\) si \(a\) et \(b\) désignent des représentants quelconques de \(A\) et de \(B\) respectivement. Ceci n'est possible bien sûr que si \(\overline{a\diamond b}\) ne dépend pas du choix des représentants \(a\) et \(b\), ce qui va imposer certaines conditions sur la relation \(\rel\). C'est l'objectif qu'il faut garder à l'esprit pour ne pas se perdre dans les méandres des constructions algébriques qui vont suivre.
Trivialement, si la loi \(\diamond\) est commutative, la compatibilité à gauche est équivalente à la compatibilité à droite.
Supposons que \({\rel}\) soit compatible avec \(\diamond\) et soit \((\overline{a},\overline{b})\in (X/{\rel})^2\). Montrons que si \(a_1\) et \(a_2\) (resp. \(b_1\) et \(b_2\)) sont deux représentants quelconques de la classe \(\overline{a}\) (resp. de la classe \(\overline{b}\)), alors \(\overline{a_1\diamond b_1}=\overline{a_2\diamond b_2}.\) On a d'une part \begin{align*} a_1&{\rel}a_2,\\ b_1&{\rel}b_2. \end{align*} et la compatibilité à droite et à gauche de \(\rel\) sur \(\diamond\) permet d'en déduire que \begin{align*} (a_1\diamond{\color{blue}b_1})&{\rel}(a_2\diamond{\color{blue}b_1})\\ ({\color{#FF8}a_2}\diamond b_1)&{\rel}({\color{#FF8}a_2}\diamond b_2). \end{align*} La transitivité de \(\rel\) nous donne \((a_1\diamond{\color{blue}b_1}){\rel}({\color{#FF8}a_2}\diamond b_2)\) soit \(\overline{a_1\diamond b_1}=\overline{a_2\diamond b_2}\) d'après cet exercice. La loi de composition \(*\) sur le quotient peut donc être définie par \begin{equation} \label{eq:loiquotient} \overline{a}\,*\,\overline{b}:=\overline{a\diamond b}. \end{equation} puisqu'elle ne dépend pas du choix des représentants \(a\) et \(b\) des classes \(\overline{a}\) et \(\overline{b}\). Grâce à la compatibilité de \({\rel}\) avec \(\diamond\), le quotient \(X/{\rel}\) peut donc hériter de la même loi que celle qui équipe \(X\) :
Par abus de langage, la loi quotient sur l'ensemble quotient est généralement notée comme la loi qui équipe l'ensemble sous-jacent.
2. Les éléments de la classe de \(0\) sont les entiers relatifs \(x\) tels que \(x\,{\rel}\,0\), c'est-à-dire ceux qui sont divisibles par \(7\) ou pour paraphraser les multiples de \(7\) : \[\overline{0}=\{7z\mid z\in\Z\}.\] On a plus généralement pour \(k\in\llbracket 0,\,6\rrbracket\) \[\overline{k}=\{7z+k\mid z\in\Z\}.\] Ces \(7\) ensembles sont deux-à-disjoints, en effet \(7z+k=7z+l\) entraîne \(k=l\). D'autre part, en anticipant sur l'étude de la division euclidienne, il existe un unique \(z\in\Z\setminus\{0\}\) et un unique \(k\in\llbracket 0,\,6\rrbracket \) tels que \(x=7z+k\). Par conséquent, les ensembles \(\overline{0},\overline{1},\ldots,\overline{6}\) sont toutes les classes d'équivalence de \(\Z\) pour la relation \({\rel}\).
3. Il faut donc prouver que \begin{equation*} \forall(x,x',y,y')\in X^4\quad (x{{\rel}}x')\wedge(y{{\rel}}y')\ \Rightarrow (x\diamond y){{\rel}}(x'\diamond y'). \end{equation*} Ce qui se traduit ici par \begin{equation*} \forall(x,x',y,y')\in X^4\quad (7\mid (x'-x))\wedge(7\mid (y'-y))\ \Rightarrow 7\mid\big((x'+y')-(x+y)\big). \end{equation*} Si \(7\mid (x'-x)\) et \(7\mid (y'-y)\), il existe \((k,l)\in\N^2\) tel que \begin{align*} 7k&=x'-x\\ 7l&=y'-y \end{align*} Et en sommant : \begin{equation*} 7(k+l)=x'+y'-(x+y). \end{equation*} Ce qui permet de conclure que la relation \({\rel}\) est compatible avec l'addition dans \(\Z\). L'ensemble quotient \(\Z/{\rel}\) peut donc être muni de la loi quotient additive héritée de celle de \(\Z\).
4. La table d'addition de \(\Z/{\rel}\) est la suivante :
| + | dim | lun | mar | mer | jeu | ven | sam |
| dim | dim | lun | mar | mer | jeu | ven | sam |
| lun | lun | mar | mer | jeu | ven | sam | dim |
| mar | mar | mer | jeu | ven | sam | dim | lun |
| mer | mer | jeu | ven | sam | dim | lun | mar |
| jeu | jeu | ven | sam | dim | lun | mar | mer |
| ven | ven | sam | dim | lun | mar | mer | jeu |
| sam | sam | dim | lun | mar | mer | jeu | ven |
La construction abstraite de l'ensemble \(\Z\) des entiers relatifs dans la section suivante est une occasion d'appliquer ces différents résultats et de mieux les comprendre.
La construction de l'ensemble des entiers relatifs est un cas particulier de symétrisation. C'est un procédé général qui a pour objectif de rajouter les éléments qui manquent à un ensemble muni d'une loi de composition afin qu'une équation du type \((\ref{eq:eqmonoide})\) admette une solution.
Considérons le monoïde \((\N,+)\). Il est commutatif par définition de l'addition dans \(\N\), la réunion ensembliste étant commutative. Soit \((n,m)\) un couple d'entiers naturels, l'équation
\begin{equation} \label{eq:symetrisation} x+n=m \end{equation}n'admet de solution dans \(\N\) que si \(m\geqslant n\). Le cas échéant, on a bien sûr envie d'écrire que cette solution est égale à \(m-n\), mais nous n'avons pas encore défini la loi soustractive \(-\), c'est précisément l'objet de cette construction. Soit \(x\) une solution de \((\ref{eq:symetrisation})\), quand elle existe. Dans ce cas, pour tout \({\color{#FF8}k}\in\N\), \(x\) est également solution de l'équation
\begin{align*} x+(n+{\color{#FF8}k})&=(m+{\color{#FF8}k}). \end{align*}Ainsi, pour \(n\) et \(m\) fixés, tous les couples de la forme \((n+{\color{#FF8}k},m+{\color{#FF8}k})\) définissent des équations \((\ref{eq:symetrisation})\) qui admettent la même solution. Il est tentant de définir la relation qui lie tous ces couples par la proposition \((n,m){{\rel}}(n',m')\Leftrightarrow n-n'=m-m'\), mais il faut l'écrire sans soustraction :
\begin{equation} \label{eq:relbin} \forall (n,m,n',m')\in\N^4\quad (n,m){{\rel}}(n',m')\Leftrightarrow n+m'=m+n', \end{equation}On définit alors l'addition sur \(\N\times\N\) qui est une loi de composition interne en conservant la même notation que pour l'addition dans \(\N\) :
\begin{equation} \label{eq:addZ} \forall (n,m,n',m')\in\N^4\quad (n,m)+(n',m') := (n+n',m+m'). \end{equation}On définit \(\Z:=(\N\times\N)\,/{\rel}\) qui, d'après le théorème de la loi quotient, est muni de la loi additive quotient puisque la relation \(\rel\) est compatible avec cette addition. On montre facilement que \((0,0)\) est l'élément neutre pour cette loi et qu'elle est associative et commutative. D'autre part, tout couple \((n,m)\) admet un symétrique, il s'agit du couple \((m,n)\), en effet
\begin{align*} (n,m)+(m,n)&=(n+m,m+n)\\ &=(n+m,n+m)\\ \text{et}\ \ (n+m,n+m)\;& {\mathscr R}\;(0,0). \end{align*}On vérifie aisément que les couples \((n,0)\) avec \(n \geqslant 0\) et les couples \((0,m)\) avec \(m > 0\) représentent des classes deux-à-deux distinctes et que ces couples représentent toutes les classes. D'autre part les classes \((0,n)\) sont les classes opposées des classes \((n,0)\) pour l'addition définie ci-dessus. On montre que le sous-ensemble de \((\Z,+)\) constitué des couples \((n,0)\) est isomorphe à \((\N,+)\), cela justifie de noter \(n\) le couple \((n,0)\). Symétriquement, on note \((-n)\) le couple \((0,n)\).
Si l'on représente le produit cartésien \(\N\times\N\) dans un repère, les représentants de type \((n,0)\) décrivent l'axe des abscisses et les représentants du type \((0,m)\) décrivent l'axe des ordonnées. La figure ci-dessous permet de visualiser les classes d'équivalence de ces couples d'entiers qui représentent les entiers relatifs de l'intervalle \([-10,10]\).
Pour achever la construction de \(\Z\), nous ne donnerons que les grandes lignes. La multiplication est définie comme suit : \[ (n,n')\times (m,m')=(nm+n'm',nm'+mn'). \] Elle a pour élément neutre \(1=(1,0)\), elle est associative et commutative et compatible avec la relation d'équivalence \({\rel}\). On vérifie que \((n,0)\times(m,0)=(nm,0)\), que \((n,0)\times(0,m)=(0,nm)\) et que \((0,n)\times(0,m)=(nm,0)\), ce qui permet de retrouver les écritures condensées usuelles puisque l'on a noté \(n\) le couple \((n,0)\) et \(-n\) le couple \((0,n)\). Pour la relation d'ordre, on peut montrer qu'il existe une seule relation d'ordre total sur \(\Z\), c'est la relation définie par \[x\leqslant y\Leftrightarrow y-x\in\N,\] qui prolonge la relation d'ordre sur les entiers naturels. On démontre que toute partie non-vide et minorée de \(\Z\) admet un plus petit élément.
Notons pour conclure cette section que le procédé de construction du corps des fractions de \(\Z\), à savoir \(\Q\) est tout à fait similaire en partant cette fois de l'équation
\begin{equation} q\times x=p. \end{equation}Nous allons aborder une dernière structure dans ce chapitre. Nous aurons besoin de la structure de groupe pour étudier le problème du taquin. D'autres structures seront abordées dans le chapitre Arithmétique. Les groupes sont omniprésents en mathématiques et font l'objet d'une attention toute particulière au point qu'une théorie à part entière leur est consacrée. Cette théorie est très utile pour résoudre de nombreux problèmes de combinatoire, de géométrie, etc. Les chimistes en font grand usage dans l'étude des structures moléculaires et leurs symétries.
L'ensemble des entiers relatifs \(\Z\) muni de l'addition est un groupe, de surcroît commutatif (on dit aussi groupe abélien*Niels Henrik Abel fut un mathématicien norvégien qui a démontré, entre autres, que l'on ne pouvait pas résoudre une équation de degré \(\geqslant 5\) par radicaux.). Nous reviendrons en détail sur ce groupe en arithmétique. Le sous-ensemble \(\{-1,1\}\) de \(\Z\) muni de la multiplication est un groupe commutatif.
Par analogie avec l'addition dans \(\Z\), quand la loi de groupe est notée additivement, on note souvent \(0\) l'élément neutre au lieu de \(e\) et on parle d'opposé d'un élément \(x\) plutôt que de symétrique que l'on note généralement \((-x)\). De même, quand la loi de groupe est notée multiplicativement, on note souvent \(1\) l'élément neutre au lieu de \(e\) et on parle d'inverse d'un élément \(x\) plutôt que de symétrique, que l'on note généralement \(x^{-1}\). Par abus de langage, on parle souvent du groupe \(G\) pour signifier \((G,\diamond)\), confondant ainsi le groupe avec l'ensemble sous-jacent.
Soit \((G,\diamond)\) et \((G',\star)\) deux groupes notés multiplicativement et \(f:G\rightarrow G'\) un morphisme de groupes. On vérifie que l'image de l'élément neutre \(e\) de \((X,\diamond)\) est l'élément neutre \(e'\) de \((X',\star)\), i.e.
\begin{equation} \label{eq:imneutre} f(e)=e'. \end{equation}On vérifie que l'image du symétrique \(x^{-1}\) de \(x\) est le symétrique de l'image de \(x\), i.e.
\begin{equation} \label{eq:iminverse} f(x^{-1})={f(x)}^{-1}. \end{equation}D'autre part, pour tout entier relatif \(n\in\Z\), on a
\begin{equation} f(x^n)=(f(x))^{n}. \end{equation}L'ensemble des entiers relatifs \(\Z\) est un groupe commutatif pour l'addition, et \(\Z\setminus\{0\}\) n'est pas un groupe pour la multiplication. En revanche l'ensemble des réels \(\R\) est un groupe commutatif pour l'addition et \(\R\setminus\{0\}\) est un groupe commutatif pour la multiplication.
Le sous-ensemble \(\{-1,1\}\) de \(\Z\) muni de la multiplication induite est un sous-groupe de \((\Z,\times)\). L'ensemble \(3\Z:=\{3k\mid k\in\Z\}\) des multiples de \(3\) muni de l'addition est un sous-groupe de \((\Z,+)\).
Si \(H\) est un sous-groupe de \(G\), l'injection canonique \(j:H\rightarrow G\) vérifie \(j(x\diamond y)=j(x)\diamond j(y)\), c'est donc un morphisme de groupes. Et d'après \((\ref{eq:imneutre})\) et \((\ref{eq:iminverse})\), l'élément neutre de \(H\) est celui de \(G\) et le symétrique d'un élément de \(H\) est le même que son symétrique dans \(G\) ce qui prouve la proposition suivante :
Le théorème suivant est particulièrement utile, il fournit plusieurs caractérisations d'un sous-groupe, soit autant de pistes pour démontrer qu'un sous-ensemble \(H\subseteq G\) muni de la loi induite par celle du groupe \((G,\diamond)\) est bien un sous-groupe de \(G\).
Montrons que \((2)\then(3)\). C'est évident puisque \(e\in H\).
Montrons que \((3)\then(4)\). C'est évident puisque \(y^{-1}\in H\) et que \(H\) est stable.
Montrons que \((4)\then(2)\). Puisque \(H\) n'est pas vide, il existe au moins un \(x\in H\), on peut donc appliquer la deuxième partie de l'hypothèse sur le couple \((x,x)\), soit \(x\diamond x^{-1}=e\in H\). On peut à présent appliquer la deuxième partie de l'hypothèse au couple \((e,x)\), soit \(e\diamond x^{-1}=x^{-1}\in H\). Pour la stabilité, \(x\diamond y=x\diamond(y^{-1})^{-1}\).
On conclut avec \((2)\then(1)\). \(H\) étant stable la loi \(\diamond\) induite sur \(H\) est associative et admet \(e\) pour élément neutre et tout \(x\in H\) admet pour symétrique \(x^{-1}\).
Si \((G,\diamond)\) est un groupe, \((G,\diamond)\) est évidemment un sous-groupe de \((G,\diamond)\), c'est le plus grand élément pour la relation \(\subseteq.\) Pour cette même relation d'ordre, le plus petit sous-groupe de \(G\) est le sous-groupe \((\{e\},\diamond)\) où \(e\) est l'élément neutre de \(G\) pour la loi \(\diamond\). On vérifie aisément que si \(H\) est un sous-groupe de \(G\) qui est lui même un sous-groupe de \(K\), alors \(H\) est un sous-groupe de \(K\).
L'intersection d'une famille de sous-groupes d'un groupe \(G\) est un sous-groupe de \(G\). Soit \(A\subseteq G\) une partie d'un groupe \(G\), l'intersection de tous les sous-groupes de \(G\) qui contiennent \(A\) n'est jamais vide puisque \(G\) est un sous-groupe de \(G\) et contient \(A\).
On admettra le théorème suivant :
L'image et le noyau d'un morphisme fournissent des critères simples pour décider s'il est surjectif ou injectif, ce qui s'avère très utile en pratique :
On rappelle que le centre de \(G\) est la partie \(Z_G\) des éléments de \(G\) qui commutent avec tous les éléments du groupe, i.e.
\[Z_G=\{a\in G\mid\forall x\in G\ \ x\diamond a=a\diamond x\}\]Soit \(a\in Z_G\), on a donc \(\forall x\in G\ \ x\diamond a = a \diamond x\) et en composant à droite par le symétrique de \(a\) noté \(a^{-1},\) on a nécessairement
\[\forall x\in G\ \ x=a\diamond x\diamond a^{-1}.\]2. On a \(\varphi_a\circ\varphi_{a^{-1}}=\varphi_{a^{-1}}\circ\varphi_a={\Id}_G\), donc \(\varphi_a^{-1}=\varphi_{a^{-1}}\).
3. Soit \((a,b)\in G^2\). On a \(\varphi(a\diamond b)=\varphi_{a\diamond b}\), or \(\forall x\in G\), \begin{align*} \varphi_{a\diamond b}(x) &= (a\diamond b)\diamond x \diamond (a\diamond b)^{-1}\\ &= (a\diamond b)\diamond x \diamond (b^{-1}\diamond a^{-1})\\ &= a\diamond(b\diamond x\diamond b^{-1})\diamond a^{-1}\\ &= \varphi_a(b\diamond x\diamond b^{-1})\\ &= \varphi_a(\varphi_b(x))\\ &= (\varphi_a\circ\varphi_b)(x) \end{align*} Donc \(\varphi(a\diamond b)=\varphi_a\circ\varphi_b\).
4. Par définition \(\text{Ker}(\varphi)=\{a\in G\mid \varphi_a={\Id}_G\}.\) Mais \(\varphi_a={\Id}_G\) est équivalent à \begin{equation*} \forall x\in G\ \varphi_a(x)=x\ \iff\ \forall x\in G\ a\diamond x\diamond a^{-1}=x \iff\ \forall x\in\ G\ a\diamond x=x\diamond a. \end{equation*} Ce qui prouve que \(\text{Ker}(\varphi)=Z(G)\).
Soit \(G\) un groupe, \(a\in G\) et \(H\) et \(H'\) deux sous-groupes de \(G\). On dit que \(H\) et \(H'\) sont conjugués par \(a\) si et seulement si \(H'=aHa^{-1}\).
Autrement dit, un sous-groupe est normal s'il est égal à tous ses conjugués. Si \((G,\diamond)\) est un groupe d'élément neutre \(e\), alors \((\{e\},\diamond)\) et \((G,\diamond)\) sont deux sous-groupes normaux de \((G,\diamond),\) dits triviaux et s'il n'y en a pas d'autres, alors \((G,\diamond)\) est appelé un groupe simple. Les groupes simples et finis jouent un rôle majeur dans l'étude générale des groupes finis, car ces derniers sont tous construits à partir de ces groupes simples. Leur très difficile classification a demandé des dizaines d'années de recherche et s'est achevée au début des années 1980.
Si un groupe \(G\) est commutatif, tous ses sous-groupes sont normaux, cette notion a donc surtout un intérêt dans l'étude des groupes non-commutatifs. On sait déjà que l'image ou l'image réciproque d'un sous-groupe par un morphisme de groupe est un sous-groupe et on peut montrer que l'image et l'image réciproque d'un sous-groupe normal par un morphisme de groupe sont des sous-groupes normaux. En corollaire, le noyau d'un morphisme de groupe est toujours un sous-groupe normal.
L'étude des sous-groupes normaux est motivée par la caractérisation des relations d'équivalence qui sont compatibles avec une loi de groupe. En effet, il faut se souvenir que l'on ne peut transporter la loi de composition qui équipe l'ensemble sur l'ensemble quotient, qu'à la condition que la relation d'équivalence soit compatible avec sa loi de composition. Dans le cas particulier où le magma est un groupe, les seules relations d'équivalence compatibles avec sa loi sont entièrement caractérisées par les sous-groupes normaux de \(G\).
Les classes d'équivalence des relations \(\color{orange}{\mathscr R}_g\) et \(\color{lightblue}{\mathscr R}_d\) définies en \((\ref{eq:rgrd})\) sont respectivement les ensembles \begin{equation} a\diamond H:=\{a\diamond h\mid h\in H\}\quad\text{et}\quad H\diamond a:=\{h\diamond a\mid h\in H\}, \end{equation} appelés classes à gauche et classes à droite suivant \(H\). L'application \(x\mapsto x^{-1}\) de \(G\) dans \(G\) définit une bijection entre \(a\diamond H\) et \(H\diamond a^{-1}\), autrement dit l'ensemble des inverses des éléments de \(a\diamond H\) est l'ensemble \(H\diamond a^{-1}\). Par conséquent, les deux ensembles quotients \(G/{\mathscr R}_g\) et \(G/{\mathscr R}_d\) sont équipotents et s'ils sont finis leur cardinal est appelé indice de \(H\) dans \(G\), on le note \((G:H)\) ou \([G:H]\) ou encore \(|G:H|\). Le théorème de Lagrange qui va suivre est un résultat fondamental, il est omniprésent dans les raisonnements qui concernent les groupes finis.
Soit \({\rel}\) une relation d'équivalence compatible avec la loi \(\diamond\), autrement dit compatible à gauche et à droite. Soit \(H\) la classe d'équivalence de l'élément neutre \(e\). On sait que \(H\) est un sous-groupe de \(G\) et que \(\forall x\in G\), \(x{{\rel}}y\) si et seulement si \(y\in x\diamond H\) et \(y\in H\diamond x\), soit
\begin{equation*} \forall x\in G\quad x\diamond H=H\diamond x, \end{equation*}soit \(H\trianglelefteq G\). Réciproquement si \(H\trianglelefteq G\), la relation \({\rel}\) définie par \(x{{\rel}}y\) si et seulement si \(x^{-1}\diamond y\in H\) qui équivaut à \(y\diamond x^{-1}\in H\) est compatible avec la loi \(\diamond\). Par conséquent :
Puisque les relations d'équivalence compatibles avec une loi de groupe sont complètement caractérisées par les sous-groupes normaux du groupe, le groupe quotient est noté \(G\,/\,H\) plutôt que \(G\,/\,{\rel}\). D'autre part, la surjection canonique \(\varphi:G\rightarrow G\,/\,H\) est un morphisme de groupes.
Nous savons déjà que tout sous-groupe d'un groupe commutatif est normal. \((\Z,+)\) est un groupe commutatif, les relations d'équivalence compatibles avec l'addition sur \(\Z\) sont donc du type \[x{{\rel}}y\Leftrightarrow y-x\in H\] où \(H\) est un sous-groupe de \(\Z\). L'étude de ce groupe particulier est le point de départ de l'arithmétique, ce que nous aborderons au chapitre éponyme Arithmétique.
L'ensemble des permutations des éléments d'un ensemble joue un rôle très important en informatique. Par exemple, tous les algorithmes de tri sont intimement reliés à l'étude de cet ensemble. Nous verrons d'ailleurs que beaucoup de résultats mathématiques de cette section ne sont rien d'autres que des algorithmes déjà connus du lecteur sans avoir pour autant étudié le groupe symétrique.
Si deux ensembles \(X\) et \(Y\) sont équipotents, étudier le groupe symétrique de l'un est équivalent à étudier celui de l'autre. En effet si \(f:X\rightarrow Y\) est une bijection alors l'application \(\varphi:{S}(X)\rightarrow{S}(Y)\) définie par \(\sigma\mapsto f\circ \sigma\circ f^{-1}\) est un isomorphisme de groupes. En particulier, si un ensemble est fini de cardinal \(n\), l'étude de son groupe symétrique peut toujours se ramener à l'étude du groupe symétrique \(S_n\) de degré \(n\). Ceci montre que l'étude du groupe symétrique \({S}_n\) de degré \(n\) ne se limite pas à l'étude des permutations des éléments de l'ensemble \(\llbracket 1,\,n\rrbracket \) mais concerne tous les ensembles finis de cardinal \(n\).
Le théorème de Cayley* Arthur Cayley était un mathématicien anglais. ci-dessous va plus loin et affirme que n'importe quel groupe peut être assimilé à un sous-groupe du groupe symétrique, justifiant l'intérêt que l'on accorde à ce groupe.
Nous allons nous concentrer sur le groupe symétrique d'un ensemble fini et particulièrement sur le groupe \(\Sn_{n}\) de degré \(n\). On représente généralement le graphe d'une permutation \(\sigma\in{S}_n\) sous la forme d'une matrice de 2 lignes de \(n\) entiers dont la première ligne contient tous les entiers de \(1\) à \(n\) dans l'ordre croissant et la seconde leurs images en vis-à-vis :
\begin{equation} \sigma=\begin{pmatrix} 1&2&3&\cdots&n\\ \sigma(1)&\sigma(2)&\sigma(3)&\cdots&\sigma(n) \end{pmatrix} \end{equation}C'est un résultat à ne pas perdre de vue. Le fait que ce groupe ne soit pas commutatif en général lui donne un intérêt tout particulier et le théorème de Cayley montre que l'étude du groupe symétrique et de ses sous-groupes permet indirectement d'étudier tous les groupes.
Si \(\sigma\in Z(S_n)\), on peut appliquer \((\ref{eq:compotau})\) à n'importe quel couple de valeurs \((a,b)\) distinctes de l'intervalle \(\ab{1}{n}\), en particulier \((1,2)\) :
La loi de composition des applications se comporte de manière similaire à un produit, ainsi pour alléger les écritures, le symbole de composition des applications \(\circ\) sera écrit comme un produit et très souvent omis dans les expressions. On parlera donc du produit \(\sigma\tau\) au lieu de la composition \(\sigma\circ\tau\) de \(\sigma\) et \(\tau\).
Soit \(k\in\N\). Si \(k\geqslant 0\), la notation \(\sigma^k\) désigne la \(k\)-ème itérée de \(\sigma\), i.e. la composition de \(k\) termes \(\sigma\) et la notation \(\sigma^{-k}\) la \(k\)-ème itérée de la permutation inverse \(\sigma^{-1}\).
La proposition suivante va nous permettre d'élaborer un algorithme pour construire l'orbite \(\orb_\sigma(x)\) d'un élément \(x\) de \(\llbracket 1,\,n\rrbracket \) suivant une permutation \(\sigma\in\Sn_n\).
Cette proposition montre que pour construire l'orbite d'un élément \(x\), il suffit d'itérer ses images par \(\sigma\) tant que la nouvelle image obtenue est différente de \(x\). Considérons par exemple la permutation \(\sigma\in\Sn_{9}\) suivante :
\begin{align} \label{def:perm1} \sigma=\begin{pmatrix} \color{#FF8}1&\color{#F44}2&\color{#FF8}3&\color{#FF8}4&\color{#AAF}5&\color{#AAF}6&\color{#8DF}7&\color{#FF8}8&\color{#AAF}9\\ \color{#FF8}3&\color{#F44}2&\color{#FF8}8&\color{#FF8}1&\color{#AAF}6&\color{#AAF}9&\color{#8DF}7&\color{#FF8}4&\color{#AAF}5 \end{pmatrix}. \end{align}Calculons l'orbite de \(\color{#FF8}1\). On a \(\sigma({\color{#FF8}1})=3\), puis \(\sigma({\color{#FF8}3})=8\), puis \(\sigma({\color{#FF8}8})=4\) et finalement \(\sigma(4)=1.\) On obtient de cette façon quatre orbites pour cette permutation :
\begin{align*} \orb_\sigma({\color{#FF8}1})&=\{{\color{#FF8}1,3,8,4}\},\\ \orb_\sigma({\color{#F44}2})&=\{{\color{#F44}2}\},\\ \orb_\sigma({\color{#AAF}5})&=\{{\color{#AAF}5,6,9}\},\\ \orb_\sigma({\color{#8DF}7})&=\{{\color{#8DF}7}\}.\\ \end{align*}La représentation sagittale du graphe de cette permutation permet de mieux visualiser les différentes orbites et l'origine du vocabulaire employé :

Le support de la permutation \(\sigma=[3,2,8,1,6,9,7,4,5]\) définie en \((\ref{def:perm1})\) est \(\text{supp}(\sigma)=\{{\color{#FF8}1},{\color{#FF8}3},{\color{#FF8}8},{\color{#FF8}4},{\color{#AAF}5},{\color{#AAF}6},{\color{#AAF}9}\}\). Le support de la permutation identique est l'ensemble vide.
La permutation \(\sigma=[3,2,8,1,6,9,7,4,5]\) définie en \((\ref{def:perm1})\) n'est pas un cycle mais en contient deux : un \(4\)-cycle et un \(3\)-cycle.
À ce stade, nous savons que la restriction d'une permutation \(\sigma\) à une orbite \(\orb{}\) est une bijection (cf. exercice), c'est donc une permutation définie sur l'ensemble \(\orb{}\). En notant \(x_1\) un représentant de \(\orb{}\) et en définissant par récurrence \(x_{k+1}:=\sigma(x_k)\), l'assertion \((\ref{eq:calculorb})\) montre que cette restriction est de la forme
\begin{equation} \label{eq:circulante} \sigma=\begin{pmatrix} x_1&x_2&\cdots&x_{p-1}&x_p\\ x_2&x_3&\cdots&x_{p}&x_1 \end{pmatrix} \end{equation}Ceci explique pourquoi on a qualifié de cycle une telle permutation (on déplace tous les étudiants d'une rangée d'une place sur leur gauche et le dernier étudiant se place en première position sur la rangée). On en déduit qu'un \(p\)-cycle opère un décalage circulaire sur les éléments de son orbite et laisse fixes les \(n-p\) éléments restants. Ceci justifie que l'on note un \(p\)-cycle \(\sigma\) par le \(p\)-uplet \[(x_1,x_2,\ldots,x_p)\] qui le caractérise puisque \(\sigma(x_i)=x_{i+1}\) pour \(i\in\ab{1}{p-1}\) et \(\sigma(x_p)=x_1\). Une transposition \((x_i,x_j)\) est parfois notée \(\tau_{x_i,x_j}\).
On déduit de l'étude menée le théorème suivant, qui est l'homologue du théorème fondamental de l'arithmétique affirmant que tout entier naturel se décompose de manière unique, à l'ordre près des facteurs, en produit de facteurs premiers.
La première propriété du lemme ci-dessus est très importante. L'analogie permanente entre le calcul sur les nombres et sur les permutations (produit, décomposition, etc.) peut nous fourvoyer car le produit de nombres (entiers, réels, complexes, etc.) est commutatif alors que la composition des applications ne l'est pas ! Il est en effet tentant d'écrire par réflexe \({\color{red}(\sigma\,\tau)^2=\sigma^2\,\tau^2}\) où \(\sigma\) et \(\tau\) sont deux permutations, alors que \begin{align*} (\sigma\,\tau)^2 &=(\sigma\,\tau)\,(\sigma\,\tau)\\ &=\sigma\,({\color{orange}\tau\,\sigma})\,\tau \end{align*} et qu'en général \({\color{orange}\tau\,\sigma\neq\sigma\,\tau}\), sauf précisément si les supports des permutations \(\tau\) et \(\sigma\) sont disjoints.
Les différents résultats obtenus montrent que l'algorithme que nous avons appliqué pour calculer les différentes orbites détermine également les différents cycles puisque nous avons calculé chaque orbite en itérant la permutation \(\sigma\).
Soit sous forme matricielle :
Il y a et on obtient la décomposition en produit de cycles à supports deux-à-deux disjoints suivante :
on en déduit une décomposition en produit de transpositions :
La signature de cette permutation est égale à
L'ordre de cette permutation est égal à
et son type est égal à
Le théorème suivant est un résultat bien connu du lecteur, il est simplement masqué par le vocabulaire des permutations. Il dit en substance que l'on peut réorganiser les livres de sa bibliothèque comme on le souhaite en ne permutant jamais plus de deux livres à la fois, ce qui est bien pratique quand on n'a que deux mains.
Le théorème précédent affirmait que l'on pouvait réorganiser sa bibliothèque en ne permutant que deux livres à la fois, le théorème suivant affirme que l'on peut encore y arriver si ces deux livres sont toujours côte à côte.
On se donne une liste* Une séquence. \(L\) de \(n\) valeurs d'ensemble d'indexation \(\ab{1}{n}\), dans un ensemble totalement ordonné \((X,\preceq)\). On cherche à trier les \(n\) valeurs \(L[i],\ i\in\ab{1}{n}\) de cette liste dans l'ordre croissant.
Pour étudier un algorithme basé sur des comparaisons entre éléments de \(X\), on peut toujours supposer que \(X=\ab{1}{n}\) et qu'il est muni de l'ordre naturel \(\leq\). En effet, l'ordre sur \(X\) étant total, on peut toujours numéroter les \(n\) éléments \(x_1,x_2,\ldots,x_n\) de la liste \(L\) de sorte que \[ \forall (i,j)\in\ab{1}{n}^2 \quad (i \leqslant j)\ \then\ (x_i \preceq x_j). \] ce qui définit un morphisme d'ensembles ordonnés entre \((\ab{1}{n} ,\leq)\) et \((L(\ab{1}{n}),\preceq)\) où \(L(\ab{1}{n})\) est l'ensemble des valeurs de la liste \(L\) (l'image de l'application \(L\)). En triant les valeurs entières, on trie donc les éléments de la liste à travers ce morphisme. Pour illustrer le propos, tout algorithme de tri comparatif opère de la manière pour trier la liste \(L=[3,9,4,2]\) que pour trier la liste \[L=[\underset{3}{2},\underset{9}{4},\underset{4}{3},\underset{2}{1}],\] le morphisme en question de \(\ab{1}{4}\rg\{3,9,4,2\}\) étant défini par \(1\mapsto 2\), \(2\mapsto 3\), \(3\mapsto 4\) et \(4\mapsto 9\). La valeur importe peu, ce sont les positions relatives des valeurs pour la relation d'ordre qui déterminent le comportement de l'algorithme.
Par conséquent, on peut supposer que la liste \(L\) de longueur \(n\) contient exactement les \(n\) entiers de \(1\) à \(n\), autrement dit \(L\) code explicitement une permutation du groupe symétrique \(\Sn_n\) :
\begin{equation} L=\begin{pmatrix} 1&2&3&\ldots&n\\ L[1]&L[2]&L[3]&\ldots&L[n] \end{pmatrix}. \end{equation}Pour trier \(L\), on suppose que l'on dispose d'une opération \(i\overset{L}{\rightleftharpoons} j\) qui échange le contenu des cellules d'indices \(i\) et \(j\) de la liste \(L\). Cette opération est réalisée par l'algorithme suivant :
Algorithme Echanger(@L,i,j): aux ← L[i] L[i] ← L[j] L[j] ← aux
On connaît évidemment le résultat des courses puisque la liste triée est la liste \([1,2,\ldots,n]\), c'est-à-dire la permutation identité. Mais ce n'est pas tant le résultat du tri qui nous motive ici, que la manière de le réaliser. L'échange \(i\overset{L}{\rightleftharpoons} j\) définit implicitement la transposition \((L[i],L[j])\) et un algorithme de tri comparatif opère en une séquence finie d'échanges, donc de transpositions. Notons \((\tau_k)_{k\in\ab{1}{t}}\) les \(t\) échanges réalisés pour trier la liste \(L\). On vient de montrer que \begin{align*} \tau_t\,\tau_{t-1}\,\ldots\,\tau_2\,\tau_1\, L &= {\Id},\\ L &= {\Id}\,(\tau_t\,\tau_{t-1}\,\ldots\,\tau_2\,\tau_1)^{-1},\\ L &= \tau_1\,\tau_2\,\ldots\,\tau_{t-1}\,\tau_t \quad\text{car}\ (s\,t)^{-1}=t^{-1}\,s^{-1}\ \text{et}\ \tau_i=\tau_i^{-1}. \end{align*} Nous venons donc de décomposer la permutation \(L\) en produit de transpositions. Chaque algorithme de tri comparatif in situ*qui échange les valeurs dans la liste constitue donc une preuve constructive que toute permutation se décompose en un produit de transpositions. On comprend mieux à présent pourquoi la décomposition d'une permutation en produit de transpositions n'a rien d'unique vu la diversité des algorithmes de tris comparatifs.
L'algorithme du tri par propagation également appelé tri à bulles, réalise le tri d'une liste uniquement avec des échanges du type \(i\rightleftharpoons i+1\). Le principe est simple, pour toutes les valeurs \(k\) allant de \(n\) à \(2\), on balaie la liste \(L\) de \(i\leftarrow 1\) à \(k\) en faisant l'échange \(i\rightleftharpoons i+1\) si \(L[i+1] \preceq L[i]\).
La grande variété des preuves/algorithmes de tris est due à la recherche d'une décomposition en produit de transpositions qui minimise le nombre de comparaisons et/ou d'échanges entre éléments de la liste.
Dans la suite \(X\) désigne un ensemble fini de cardinal \(n\).
La permutation identité génère \(n\) orbites puisque tous les points sont fixes, donc \(\epsilon({\Id}_X)=(-1)^{n-n}=1\). Une transposition \(\tau\) laisse \(n-2\) points fixes et crée une orbite de cardinal \(2\), il y a donc au total \(n-1\) orbites, d'où \(\epsilon(\tau)=(-1)^{n-(n-1)}=-1\). Un \(p\)-cycle \(\sigma\) laisse \(n-p\) points fixes et crée une unique orbite de taille \(p\), il y a donc \(n-p+1\) orbites, donc \(\epsilon(\sigma)=(-1)^{n-(n-p+1)}=(-1)^{p-1}\).
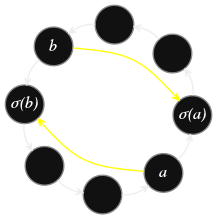
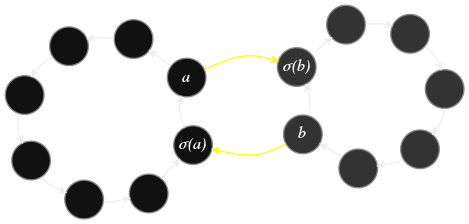
Supposons dans un premier temps que \(\{a,b\}\subseteq\orb\) et notons \(p:=|\orb|\geqslant 2\). Dans ce cas \(a\) (et \(b\)) est un représentant de l'orbite \(\orb\) donc \[\orb=\orb(a)=\{a,\sigma(a),\ldots,\sigma^{p-1}(a)\}\quad\text{et}\ \ \sigma^p(a)=a. \]
Puisque \(b\in\orb(a)\), \(b=\sigma^q(a)\) avec \(0 \lt q\leqslant p\). Calculons les itérés successifs de \(a\) par la permutation \(\sigma'\). On a \begin{align*} \sigma'(a) &=\sigma(\tau(a)),\\ &=\sigma(b),\\ &=\sigma^{q+1}(a). \end{align*}
et \(\sigma'(\sigma^{q+1}(a))=\sigma(\tau(\sigma^{q+1}(a)))\), mais \(\sigma^{q+1}(a)\not\in\{a,b\}\), or la restriction de la transposition \(\tau_{a,b}\) à \(X\setminus\{a,b\}\) est l'identité, donc \[\sigma'(\sigma^{q+1}(a))=\sigma^{q+2}(a)\] et de proche en proche on obtient montre que l'orbite de \(a\) selon \(\sigma'\) est \[a,\;\sigma^{q+1}(a),\;\sigma^{q+2}(a),\;\ldots,\;\sigma^{p-2}(a),\;\sigma^{p-1}(a),\; a.\] Tandis que les itérés de \(b\) selon \(\sigma'\) sont \[b,\;\sigma(b),\;\sigma^2(b),\;\ldots,\;\sigma^{q-1}(b),\;b.\] Autrement dit, l'orbite \(\orb\) a été séparée en deux orbites.
Dans l'autre cas (à droite sur la figure), on a \begin{align*} \orb&=\{a,\sigma(a),\sigma^2(a),\ldots,\sigma^{p-1}(a)\},\\ \orb'&=\{b,\sigma(b),\sigma^2(b),\ldots,\sigma^{q-1}(b)\}.\\ \end{align*}
Si on calcule les itérés de \(a\) pour \(\sigma'\), on obtient \[a,\;\sigma(b),\;\sigma^2(b),\;\ldots,\sigma^{q-1}(b),\;b,\;\sigma(a),\;\sigma^2(a),\;\ldots,\;\sigma^{p-1}(a),\;a.\] Autrement dit les orbites \(\orb\) et \(\orb'\) ont fusionné. Dans les deux cas le nombre d'orbites suivant \(\sigma'\) est différent du nombre d'orbites suivant \(\sigma\) d'une unité ce qui change donc le signe de la signature et permet de conclure.
Il faut donc déduire de ce corollaire que la signature d'un produit (au sens de la composition des applications) de permutations est le produit (au sens des nombres entiers) de leurs signatures.
Soit \(\tau\) une transposition. L'application de \(\A(X)\) dans \(\Sn(X)\setminus\A(X)\) définie par \(\sigma\mapsto\tau\sigma\) est une bijection et comme ces deux ensembles constituent une partition de \(\Sn(X)\) qui est de cardinal \(n!\), on a nécessairement
\begin{equation} |A(X)|=|\Sn(X)\setminus A(X)|=\frac{n!}{2}. \end{equation}Autrement dit il y a autant de permutations paires que de permutations impaires. Dans le cas où \(\Sn(X)=\Sn_{n}\), le sous groupe alterné est noté \(A_n\) ou \(\A_n\) et on l'appelle groupe alterné de degré n.
Deux permutations \(\sigma\) et \(\sigma'\) sont conjuguées s'il existe une permutation \(\rho\) telle que \(\sigma'= \rho\,\sigma\,\rho^{-1}\). Cela signifie que l'on peut réaliser la permutation \(\sigma'\) à travers la permutation \(\sigma\) au prix de deux traductions réciproques. Métaphoriquement, pour calculer \(\sigma'(x)\) on traduit \(x\) en \(\rho^{-1}(x)\), on fait le calcul avec \(\sigma\), puis on traduit le résultat avec \(\rho\). La relation de conjugaison est définie pour tout type de groupe, nous avons déjà vu qu'il s'agit d'une relation d'équivalence.
Calculons tout d'abord l'image des éléments \(\rho(x_i)\), \(i\in\llbracket 1,\,p\rrbracket \) par les deux permutations de part et d'autre de l'égalité \((\ref{eq:conjuguecycle})\) : \begin{align} \rho(x_1,x_2,\ldots,x_p)\rho^{-1}(\rho(x_i)) &=\rho(x_1,x_2,\ldots,x_p)(x_i)\\ &=\begin{cases} \rho(x_{i+1})&\text{si}\ i < p,\\ \rho(x_1)&\text{si}\ i = p. \end{cases} \end{align} D'autre part, \begin{align} (\rho(x_1),\rho(x_2),\ldots,\rho(x_p))(\rho(x_i)) &=\begin{cases} \rho(x_{i+1})&\text{si}\ i < p,\\ \rho(x_1)&\text{si}\ i = p. \end{cases} \end{align} On passe aux éléments \(x\in X\setminus Y\). On remarque que \(\forall i\in\llbracket 1,\,p\rrbracket \ \rho^{-1}(x)\not=x_i\) sans quoi \(x=\rho(x_i)\) ce qui contredit \(x\in X\setminus Y\), donc \(\rho^{-1}(x)\) n'appartient pas au support du cycle \((x_1,x_2,\ldots,x_p)\), il est donc un point fixe de ce cycle : \begin{align*} \rho(x_1,x_2,\ldots,x_p)\rho^{-1}(x)=\rho(\rho^{-1}(x))=x. \end{align*} D'autre part \(x\) est fixe pour le cycle \((\rho(x_1),\rho(x_2),\ldots,\rho(x_p))\) puisque \(x\not\in Y\), donc \begin{align*} (\rho(x_1),\rho(x_2),\ldots,\rho(x_p))(x)=x \end{align*}
Notons \(n_i\) le nombre d'orbites de cardinal \(i\in\ab{1}{n} \) suivant la permutation \(\sigma\in\Sn_n\). Les orbites formant une partition de \(\ab{1}{n} \), la formule de sommation nous donne
\begin{equation} n=\sum_{i=1}^nn_i. \end{equation}D'autre part, le type \((p_1,p_2,\ldots,p_k)\) de la permutation \(\sigma\) contient la taille de chaque orbite qui n'est pas réduite à un élément. Autrement dit le nombre \(n_1\) de points fixes de la permutation \(\sigma\), c'est-à-dire le nombre d'orbites réduites à un singleton est donné par
\begin{equation} n_1=n-\sum_{i=1}^k p_i. \end{equation}Ceci justifie que le type d'une permutation se dispense de faire apparaître les longueurs 1 des orbites réduites à un élément.
Nous avons vu que la permutation conjuguée d'un cycle par une permutation \(\rho\) est le cycle constitué des images des éléments du cycle par \(\rho\), cf. \((\ref{eq:conjuguecycle})\). Par conséquent :
On en déduit immédiatement que le nombre de types de permutations du groupe \(\Sn_n\) distincts est égal au nombre de façons possibles d'écrire l'entier \(n\) comme la somme d'une suite croissante d'entiers non-nuls. Une telle somme est qualifiée de partition d'un entier. Par exemple, pour \(n=4\), on vérifie aisément que l'on a exactement les \(5\) partitions suivantes :
\begin{align*} 4 &=1+1+1+1\quad\text{type vide}\ (\,)\\ &=1+1+2\quad\text{type}\ (2)\\ &=2+2\quad\text{type}\ (2,2)\\ &=1+3\quad\text{type}\ (3)\\ &=4\quad\text{type}\ (4) \end{align*}Le type vide est celui de la permutation identité.
En corollaire, on sait à présent que le nombre de partitions \(p(n)\) d'un entier \(n > 0\), c'est-à-dire le nombre de type différents de permutations est égal à \begin{equation} p(n)=\sum_{k=1}^np(n,k). \end{equation}
Autrement dit, tout couple \((i,j)\) tel que \(i\lt j\) est, soit une inversion de \(\sigma\), soit une inversion de \(\overline{\sigma}\), il y a donc \(\frac{n(n-1)}{2}\) inversions (voir exercice ci-dessus) réparties entre \(\sigma\) et \(\overline{\sigma}\). Si on somme sur tous \(\sigma\in S_n\), on a donc au total \(n!\,\frac{n(n-1)}{2}\) inversions, mais chaque permutation de \(S_n\) a été comptée deux fois puisque l'opération miroir est une bijection de \(S_n\). Il y a donc finalement \[n!\ \frac{n(n-1)}{4}.\] inversions au total.
Ces résultats seront utiles dans l'analyse de la complexité des algorithmes de tri en particulier.
Nous pouvons à présent étudier le problème du taquin et répondre à la question initiale. On numérote les cases du taquin dans l'ordre de lecture (cf. tableau à gauche ci-dessous), et on numérote également les 15 pièces du taquin de \(1\) à \(15\). Le numéro \(16\) est attribué à une pièce virtuelle, la pièce vide.
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 15 | 14 |
En associant à chaque numéro de case du taquin le numéro de la pièce qui y est placée, la disposition des \(16\) pièces sur le taquin définit une permutation \(\sigma\in\Sn_{16}\). On l'appelera dans la suite la configuration du taquin. La configuration du taquin proposée par Loyd est la permutation :
\begin{equation} \sigma=\begin{pmatrix} 1&2&3&4&5&6&7&8&9&10&11&12&13&\color{#88F}14&\color{#88F}15&16\\ 1&2&3&4&5&6&7&8&9&10&11&12&13&\color{#88F}15&\color{#88F}14&16\\ \end{pmatrix} \end{equation}Elle ne contient qu'un seul cycle d'ordre 2, c'est la transposition \({\color{#88F}(14,15)}\).
Comment se traduit le déplacement d'une pièce \(k\) sur le taquin ? Compte tenu de la règle du jeu, on ne peut échanger la pièce \(k\) qu'avec la pièce vide numérotée \(16\). Autrement dit, un mouvement, quand il est possible, est nécessairement une transposition de la forme \((k,16)\) mais cette condition n'est pas suffisante. Pour qu'une transposition \((k,16)\) soit possible, il faut également que les pièces \(k\) et \(16\) soient adjacentes, c'est-à-dire qu'elles aient un côté commun.
Soit \(\sigma\) la permutation associée à une configuration du taquin. Nous dirons qu'une transposition \(\tau\) est compatible avec la configuration \(\sigma\) si et seulement si elle est de la forme \(\tau=(16,k)\) et que les pièces \(k\) et \(16\) sont adjacentes sur le taquin. Dans ce cas, \(\tau\sigma\) est une nouvelle configuration du taquin, on dira donc plus généralement qu'une permutation \(\pi\) est compatible avec la configuration \(\sigma\) si \(\pi\) est décomposable en un produit de \(n\) transpositions \[\pi=\tau_{n}\,\tau_{n-1}\,\ldots\tau_2\,\tau_1.\] telles que \(\forall i\in\ab{1}{n} \), \(\tau_i\) est compatible avec le produit \[\tau_{i-1}\tau_{i-2}\ldots\tau_{1}\sigma.\] Ce qui signifie ni plus ni moins qu'en partant de la configuration \(\sigma\), les transpositions \(\tau_1\) puis \(\tau_2\), etc. sont possibles dans cet ordre.
Pour résoudre une configuration \(\sigma\) du taquin, et celle de Loyd en particulier, il faut donc remettre toutes les pièces dans l'ordre, c'est-à-dire trouver une suite finie \(({\color{#FF8}\tau_i})_{i\in\ab{1}{n} }\) de transpositions compatibles avec \(\sigma\) telle que son produit à gauche avec \(\sigma\) est la permutation identité, soit :
\begin{equation} \label{eq:sigmataquin} {\color{#FF8}\tau_n\,\tau_{n-1}\,\ldots\,\tau_2\,\tau_1}\sigma={\Id}. \end{equation}Isolons \(\sigma\) dans l'équation \((\ref{eq:sigmataquin})\). L'inverse d'un produit de bijections est le produit inverse des bijections réciproques (cf. exercice) et toute transposition \(\tau\) est une involution donc \(\tau^{-1}=\tau\), d'où \begin{equation} \label{eq:isolesigma} \sigma={\color{#FF8}\tau_1\,\tau_{2}\,\ldots\,\tau_{n-1}\,\tau_n}. \end{equation}
Nous dirons donc dans la suite qu'une configuration \(\sigma\) du taquin est résoluble s'il existe un produit de transpositions compatibles avec \(\sigma\) satisfaisant \((\ref{eq:isolesigma})\), insoluble sinon. Si une configuration est résoluble, les mouvements à réaliser effectivement sur le taquin sont les transpositions \(\tau_i\) dans l'ordre croissant des indices. Si un tel produit existe, sa signature doit bien sûr être égale à celle de \(\sigma\) :
\begin{align} \notag\epsilon(\sigma)&=\epsilon({\color{#FF8}\tau_1\,\tau_{2}\,\ldots\,\tau_{n-1}\,\tau_n}),\\ \notag\epsilon(\sigma)&=\prod_{i=1}^n\epsilon({\color{#FF8}\tau_i}),\\ \label{eq:lastloyd}\epsilon(\sigma)&=(-1)^n. \end{align}Ces deux dernières égalités sont justifiées par le fait que la signature d'une transposition est égale à \(-1\) et que la signature d'un produit de permutations est égal au produit des signatures de ces permutations (cf. corollaire).
La signature de la configuration de Loyd \(\sigma=(14,15)\) est égale à \(-1\) puisqu'il s'agit d'une transposition. On déduit de \((\ref{eq:lastloyd})\) que l'on doit avoir \(-1=(-1)^n,\) autrement dit que le nombre \(n\) de transpositions dans le produit \(\color{#FF8}\pi\) doit être impair. Colorions les cases du taquin pour en faire un damier noir et blanc. La configuration initiale de Loyd est :
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 15 | 14 |
Une transposition de la forme \((16,k)\) fait passer alternativement la pièce vide d'une case noire à une case blanche. Pour que la pièce vide retrouve sa position initiale 16 sur le damier, le produit \({\color{#FF8}\pi}\) doit donc nécessairement contenir un nombre pair de transpositions, la configuration de Loyd est par conséquent insoluble. Nous venons de démontrer le théorème suivant :
Une condition nécessaire pour que taquin soit résoluble est que la configuration initiale définisse une permutation \(\sigma\) du groupe alterné \(\A_{15}\), si l'on suppose que la pièce vide est en position \(16\).
Cette condition est-elle suffisante ? Il faut garder à l'esprit que pour résoudre le taquin, il faut disposer d'un produit de transpositions compatible avec la permutation \(\sigma\) associée à la configuration initiale du taquin. Par exemple, seules les transpositions \((16,12)\) et \((16,15)\) sont compatibles avec la configuration de Loyd.
Nous allons montrer dans un premier temps que le groupe alterné \(\A_n\) est engendré par les \(3\)-cycles du type \((1,2,s)\) et dans un deuxième temps que tous les trois cycles de ce type sont décomposables en produit de transpositions compatibles avec l'identité.
Les \(3\)-cycles du type \((1,2,s)\) pour \(\A_{15}\) sont au nombre de \(13\) :
\begin{equation} \label{troiscycles} (1,2,{\color{#88F}3}),\ (1,2,{\color{#88F}4}),\ (1,2,{\color{#88F}5}),\ldots,\ (1,2,{\color{#88F}14}),\ \text{et}\ (1,2,{\color{#88F}15}). \end{equation}Et nous allons prouver que l'on peut réaliser n'importe lequel de ces \(3\)-cycles sur le taquin.
Soit \(k\in\N\) tel que \(k\geqslant 2\). On appelle circuit de longueur \(k\) toute séquence \((c_i)_{i\in\llbracket 1,\,k\rrbracket }\) de cases distinctes du taquin telles que deux cases consécutives de cette suite sont toujours adjacentes et telle que \(\def\vide{{\color{#C22}16}}c_k\) est adjacente à \(c_1\). La suite des cases numéro 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, matérialisée en rouge dans le taquin ci-dessous est un circuit de longueur \(12\) :
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
Dorénavant nous noterons \(\def\tua{{\color{#F44}\tau}}\tua_i:=(16,i)\), \(i\in\ab{1}{15}\) les 15 transpositions possibles sur le taquin. Soit \(\sigma\) la permutation associée à une configuration du taquin. Si on note \(p_i\) les pièces qui sont placées sur les cases \(c_i\) d'un circuit \((c_i)_{i\in\ab{1}{k}}\) respectivement, on a donc \[\forall i\in\ab{1}{k}\quad \sigma(c_i)=p_i.\]
Exemple. On considère une configuration \(\sigma\) du taquin et le circuit \(c:=(2,3,7,11,10,9,5,1)\) de longueur 8 sur lequel sont placées les pièces \(a,\) \(b,\) \(c,\) \(d,\) \(e,\) \(f,\) \(g\) et \(\vide\) respectivement. Calculons \(\pi\sigma\) avec le produit \(\pi\) défini par \[\pi:=\tua_a\,\tua_g\,\tua_f\,\tua_e\,\tua_d\,\tua_c\,\tua_b\,\tua_a.\] La pièce vide et la pièce adjacente \(k\) de la transposition \(\tau_k\) ont leur côté commun en pointillés :
| \(a\) | \(b\) | ||
| \(g\) | \(c\) | ||
| \(f\) | \(e\) | \(d\) | |
| \(\tua_{a}\) | |||
| \(a\) | \(b\) | ||
| \(g\) | \(c\) | ||
| \(f\) | \(e\) | \(d\) | |
| \(\tua_{b}\) | |||
| \(a\) | \(b\) | ||
| \(g\) | \(c\) | ||
| \(f\) | \(e\) | \(d\) | |
| \(\tua_{c}\) | |||
| \(a\) | \(b\) | \(c\) | |
| \(g\) | |||
| \(f\) | \(e\) | \(d\) | |
| \(\tua_{d}\) | |||
| \(a\) | \(b\) | \(c\) | |
| \(g\) | \(d\) | ||
| \(f\) | \(e\) | ||
| \(\tua_{e}\) | |||
| \(a\) | \(b\) | \(c\) | |
| \(g\) | \(d\) | ||
| \(f\) | \(e\) | ||
| \(\tua_{f}\) | |||
| \(a\) | \(b\) | \(c\) | |
| \(g\) | \(d\) | ||
| \(f\) | \(e\) | ||
| \(\tua_{g}\) | |||
| \(a\) | \(b\) | \(c\) | |
| \(d\) | |||
| \(g\) | \(f\) | \(e\) | |
| \(\tua_{a}\) | |||
| \(b\) | \(c\) | ||
| \(a\) | \(d\) | ||
| \(g\) | \(f\) | \(e\) | |
On a montré que le produit \(\pi:=\tua_a\,\tua_g\,\tua_f\,\tua_e\,\tua_d\,\tua_c\,\tua_b\,\tua_a\) est compatible avec la permutation \(\sigma\) et en calculant \(\pi\,\sigma\), on a remplacé la séquence \(\color{#AAF}(a,b,c,d,e,f,g)\) par la séquence \(\color{#AAF}(b,c,d,e,f,g,a)\) sur ce circuit et il suffit d'itérer \(\pi\) pour faire tourner ces pièces autour du circuit en laissant toutes les autres fixes.
Dans le cas particulier où le circuit est un carré \(2\times 2\), on a le produit suivant (on ne représente plus les autres pièces qui sont fixes) :
| \(a\) | |
| \(c\) | \(b\) |
| \(\tua_{a}\) | |
| \(a\) | |
| \(c\) | \(b\) |
| \(\tua_{b}\) | |
| \(a\) | \(b\) |
| \(c\) | |
| \(\tua_{c}\) | |
| \(a\) | \(b\) |
| \(c\) | |
| \(\tua_{a}\) | |
| \(b\) | |
| \(a\) | \(c\) |
Ce qui réalise une rotation des trois valeurs \(\color{#AAF}(a,b,c)\). Par exemple, en partant de la configuration identité \(\sigma:={\Id}\), on obtient le \(3\)-cycle \((11,12,15)\) à l'aide des quatre transpositions : \[\tua_{15}\,\tua_{12}\,\tua_{11}\,\tua_{15}.\]
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 12 | 15 |
| 13 | 14 | 11 |
Mais nous cherchons à construire les \(3\)-cycles particuliers de \((\ref{troiscycles})\) pour engendrer le groupe \(\A_{15}\). Le lemme suivant est évident mais important.
Nous allons montrer comment obtenir le cycle \(\color{#AAF}(9,10,13)\) avec les techniques de transposition présentées. On note \(\sigma:=\tua_{14}\tua_{15}\) la permutation qui déplace la pièce vide à la case 14. On fait alors tourner \(9,\) \(10\) et \(13\) autour du circuit grâce au produit \(\tua_{13}\,\tua_{10}\,\tua_{9}\,\tua_{13}\) et on ramène la pièce vide en case 16 :
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | |
| \(\sigma\) | |||
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | |
| \(\tua_{13}\,\tua_{9}\,\tua_{10}\,\tua_{13}\) | |||
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 10 | 13 | 11 | 12 |
| 9 | 14 | 15 | |
| \(\sigma^{-1}\) | |||
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 10 | 13 | 11 | 12 |
| 9 | 14 | 15 | |
On a donc montré à l'aide d'une conjugaison que : \begin{align*} (9,10,13)&=\sigma^{-1}\,\tua_{13}\,\tua_{9}\,\tua_{10}\,\tua_{13}\,\sigma,\\ &=(\tua_{15}\,\tua_{14})\,\tua_{13}\,\tua_{9}\,\tua_{10}\,\tua_{13}\,(\tua_{14}\,\tua_{15}). \end{align*}
Le programme que vous avez pu utiliser en début de chapitre et qui résout le problème du taquin dans le cas où la permutation \(\sigma\in\A_{16}\) applique exactement la stratégie que nous venons de déployer. Résumons :
Vous pouvez voir ces étapes en faisant apparaître la console javascript dans votre navigateur (sous Chromium, il suffit de cliquer sur \(\boldsymbol\vdots\) en haut à droite, puis de sélectionner "Plus d'outils" et "Outils de développement").
Vous avez pu constater que le nombre de mouvements pour remettre les pièces dans l'ordre est conséquent, quel est le nombre minimum de déplacements nécessaires pour résoudre une configuration ? Peut-on simplifier les produits de \(3\)-cycles ?
Dans la suite, une permutation \(\sigma\in{S}_n\) est considérée comme la séquence des images \(\sigma(i)\) pour \(i\in\ab{1}{n}\) et donc codée en Python par la liste \([\sigma(1),\sigma(2),\ldots,\sigma(n)]\). Comme les indices des types énumérés commencent à 0 et pas à 1 en Python, on décrémente la valeur des images. Autrement dit la permutation \begin{pmatrix} 1&2&3&4\\ \color{#FF8}3&\color{#FF8}2&\color{#FF8}1&\color{#FF8}4 \end{pmatrix} est codée par la liste [2,1,0,3]. La saisie d'une permutation et son affichage resteront en revanche conformes aux notations mathématiques usuelles. Ainsi, pour lire et afficher une permutation, un cycle ou une orbite, vous utiliserez les fonctions suivantes :
# Lecture d'une permutation
def Lire(texte = "s = "):
chaine = input(texte)
return [int(x)-1 for x in chaine.split()]
# Formatage en chaîne
def Formater(s):
sortie = [i + 1 for i in s]
if isinstance(s,tuple):
return str(tuple(sortie))
elif isinstance(s,set):
return str(set(sortie))
else:
return str(sortie)
La fonction Lire renvoie la liste des valeurs entières décrémentées d'une unité à partir de la chaîne de caractère lue au clavier. La fonction Formater convertit une permutation, un cycle ou une orbite en chaîne de caractères après avoir incrémenté chaque valeur de la structure d'une unité.
Indication : utilisez une liste B de booléens de même longueur que s tous initialisés à False qui permettra de marquer les valeurs rencontrées en parcourant s. (Vous pourriez également convertir s en Set, l'ensemble ainsi obtenu est égal à \(\{0,1,\ldots,|s|-1\}\) si et seulement si s est une bijection.)
Indication : utilisez une liste B de \(n\) booléens initialisés à True telle que \(B[i]\) est vrai si et seulement si l'orbite de \(i\) n'a pas encore été calculée.
Indications : vous pouvez calculer la signature avec la formule du cours. On rappelle que le nombre d'orbites n'est pas nécessairement le nombre de cycles, aucun point fixe d'une permutation n'est un cycle, il constitue pourtant une orbite de taille \(1\). Vous pouvez également utiliser au préalable la décomposition en produit de cycles à supports disjoints puis décomposer chaque \(p\)-cycle en produit de \(p-1\) transpositions dont la signature est donc \((-1)^{p-1}\).
où \((a,b)\) désigne le pgcd de \(a\) et \(b\). Soit \(n\) un entier \(n\geqslant 3\). Démontrez par récurrence que pour une séquence d'entiers naturels \(a_1,a_2,\ldots, a_n\) on a
\begin{equation} \label{eq:ppcm} [a_1,a_2,\ldots,a_n]= [[a_1,a_2,\ldots,a_{n-1}],a_n]. \end{equation}