Introduction

Un premier problème

Des robots sont utilisés dans une usine de construction de véhicules automobiles et un défaut de fabrication a été relevé dans la production. Les trois robots concernés, xam, arg et bax sont dotés d'un module d'auto-diagnostic et d'un module de synthèse vo­cale et lors de leur passage à l'atelier pour la révision, ils font les assertions suivantes :

Quand un robot est défectueux, son diagnostic est toujours faux et quand il fonctionne, son diagnostic est toujours vrai. On sait qu'il y a (au moins) un robot défectueux. Quel(s) robot(s) faut-il réparer ?

L'un des objectifs de ce chapitre est de présenter l'outillage nécessaire pour répondre à ce type de question (et beaucoup d'autres), et plus gé­né­ra­le­ment d'étudier des éléments de logique qui sont indispensables dans tout cursus en in­for­ma­ti­que.

Mathématiques et langage

Les mathématiques poursuivent quatre grands objectifs :

• La construction d'objets abstraits qui servent de modèles descriptifs pour la compréhension et l'étude de phénomènes physiques.
• La recherche de propriétés de ces objets abstraits qui permettent, d'une part de s'assurer de leur adéquation avec la réalité physique, d'autre part d'anticiper des résultats concrets. Les modèles sont alors des modèles prédictifs.
• La validation de ces propriétés par des démonstrations.
• La résolution de problèmes grâce aux propriétés des objets qui ont permis de les modéliser.

Le mathématicien pur contestera peut-être cette vision appliquée. On peut en effet étudier des objets mathématiques sans autre motivation que la pratique stimulante d'un jeu intellectuel et sans qu'ils aient le moindre rapport avec une quelconque réalité. Pourtant la très grande majorité des théories ma­thé­ma­ti­ques a pour origine des problèmes bien réels engendrant de nouveaux ques­tion­ne­ments qui parfois s'épanouissent au sein de théories autonomes. La dichotomie entre ma­thé­ma­ti­ques pures et appliquées n'a donc pas de raison d'être et si distinction il y a, les deux vivent depuis long­temps en par­fai­te symbiose.

Selon la théorie de l'évolution de Lamarck, la fonction créant l'organe, le langage ma­thé­ma­ti­que s'est pro­gres­si­ve­ment structuré pour que cette science puisse se développer suivant ces quatre axes. Les ma­thé­ma­ti­ques s'imposent naturellement en in­for­ma­ti­que dès que l'on cher­che à analyser un prob­lè­me, à élaborer des méthodes de résolution et à valider les ré­sul­tats obtenus. Le langage ma­thé­ma­ti­que est constitué de plusieurs langages formels imbriqués utilisant des signes et des termes qui leur sont propres et contrairement aux lan­ga­ges in­for­ma­ti­ques, la langue naturelle reste in­dis­pen­sable pour animer la partition. Ce métalangage est totalement formaté par et pour le rai­son­ne­ment.

Les règles de construction des mots, des phrases et plus généralement des langues naturelles qui oc­cu­pent les grammairiens ont leur pendant en ma­thé­ma­ti­ques et en in­for­ma­ti­que. Les ma­thé­ma­ti­ciens se sont intéressés à la théorie de la démonstration dès le début du xx^ème siècle et les in­for­ma­ti­ciens à la théorie des lan­ga­ges dans les années 1950. Les questions sur la nature du calcul ont lar­ge­ment contribué aux interactions entre les deux disciplines dans le cadre de la théorie de la cal­cu­la­bi­li­té et l'isomorphisme de Curry-Howard établit des liens formels entre une dé­mons­tra­tion dans un système logique et un programme dans un modèle de calcul, autrement dit

Ce ré­sul­tat ne sera pro­ba­ble­ment pas de nature à rassurer l'étudiant qui espérait se débarrasser purement et simplement des mathématiques, mais il met en évidence les liens profonds qui existent entre ces fondamentaux de ces deux disciplines.

La principale différence entre une langue naturelle et le métalangage ma­thé­ma­ti­que concerne les am­bi­guï­tés et la jus­tes­se des propos. Les ambiguïtés sont inhérentes aux langues naturelles et sont d'ail­leurs largement exploitées dans la rhétorique (allusions, sous-entendus, jeux de mots, sophismes, etc.) alors qu'elles sont bannies du langage ma­thé­ma­ti­que et des lan­ga­ges de programmation. Il est in­dis­pen­sa­ble de les lever dès qu'un énoncé peut être in­ter­pré­té de différentes façons :

C'est ce qui explique la nature particulière des textes ma­thé­ma­ti­ques qui emploient des tour­nu­res de phrases rarement utilisées dans le langage commun, comme si et seulement si, deux-à-deux dis­joints, un et un seul, non-vide, etc. La logique naturelle n'est pas tout à fait celle de la lo­gi­que clas­si­que des ma­thé­ma­tiques, il existe d'ailleurs des logiques ma­thé­ma­ti­ques (dites non-clas­si­ques par opposition) dont certaines ont précisément pour objet d'être plus proches de celle que nous pra­ti­quons au quo­ti­dien. Là aussi, il est nécessaire de clarifier certaines situations. Notons que les problèmes d'interprétation de la logique ne concernent pas que les mathématiques, mais parfois les tribunaux.

Pour baptiser les objets que l'informaticien/ma­thé­ma­ti­cien construit, les mots sont choisis avec beau­coup de précaution et sont censés être en adéquation avec l'acception qu'ils ont com­mu­né­ment. Pourtant certaines distorsions existent parfois entre le sens que nous donnons à un mot et celui qu'il a en mathématiques, ce qui peut être une source d'erreurs ou de con­fu­sion. D'autre part, certains mots désignent des objets mathématiques différents selon le contexte où ils sont emp­loyés. Il faut en être conscient et comprendre le rôle réellement capital des définitions qui précisent leur sens dans un en­vi­ron­ne­ment par­ti­cu­lier. Ceci explique la structuration litanique des textes ma­thé­ma­ti­ques en al­ter­nan­ce de définitions et de théorèmes.

Pour commencer ce cours, nous allons étudier le socle logique des mathématiques et de l'in­for­ma­ti­que. Pour illustrer notre propos, nous aurons souvent besoin d'exemples qui intègrent des objets ou des notions que nous n'aurons pas encore définies formellement mais qui sont bien connues du lecteur, ou qui sont censées l'être. Ce n'est pas contraire à ce qui se fait dans tout apprentissage, la pratique de la conduite d'un véhicule est un atout pour en comprendre le fonc­tion­ne­ment. Dans la suite, si certains objets mathématiques sont construits à l'aide d'outils qui auraient dû être définis en aval, c'est pour ne pas compliquer inutilement l'exposé, cela sous-entend que ces outils ne sont pas eux-mêmes définis à l'aide de ces objets, ce qui créerait alors un cercle vicieux.

Syntaxe du calcul pro­po­si­tion­nel

Nécessité d'un cadre formel

L'étymologie du mot logique dévoile les mots raison et langage. La logique est à la base de l'ar­ti­cu­la­tion du discours ma­thé­ma­ti­que et du fonc­tion­ne­ment ato­mi­que d'un ordinateur, il n'y a rien de sur­pre­nant à ce qu'elle se soit épanouie sur le for­mi­da­ble terrain de jeu qu'est l'in­for­ma­ti­que où elle est om­ni­pré­sen­te.

Les combinaisons de pro­po­si­tions à l'aide de con­nec­teurs logiques constituent la première strate du raisonnement mathématique et de la construction des circuits électroniques. Il s'agit d'un langage à part entière, c'est le langage du cal­cul pro­po­si­tion­nel dont nous allons fixer les règles de composition. Nous aborderons d'abord les aspects mathématiques, le chapitre Calcul booléen en don­ne­ra une vision plus proche de l'in­for­ma­ti­que et de l'électronique avec l'algèbre de Boole, les fonctions boo­lé­en­nes et les circuits logiques.

De manière analogue aux langues naturelles, un énoncé ma­thé­ma­ti­que ou un programme in­for­ma­ti­que doit respecter :

• Des règles lexicales. Elles régissent l'usage des signes et symboles (l'orthographe) pour constituer des lexèmes ou unités lexicales (nombres, fonctions, identifiants, variables, opérateurs, etc.) ;
• Des règles syntaxiques. Elles régissent la composition des phrases (la grammaire) à partir des lexèmes (expressions arithmétiques, logiques, structures de contrôle, etc.) ;
• Des règles sémantiques. Tout énoncé doit être interprété, avoir une signification (un sens).

Pour commencer, nous allons mettre en évidence les problèmes liés à la sémantique de la logique en langue naturelle et qui vont nous amener à la reconsidérer dans le cadre du langage du calcul pro­po­si­tion­nel.

Il est important de noter dans cette définition informelle qu'il est possible de fixer une valeur de vérité à une pro­po­si­tion­. Une pro­po­si­tion n'a pas besoin d'une valeur de vérité pour être une pro­po­si­tion, d'autre part si valeur de vérité il y a, elle n'est pas con­sub­stan­tiel­le à la pro­po­si­tion. Certains auteurs par­lent d'assertion pour une pro­po­si­tion, mais nous préférons ici réserver ce terme pour désigner une pro­po­si­tion­ énoncée comme vraie. Une assertion est donc une affirmation, ce qui rend son usage conforme à l'ac­cep­tion de ce terme en français.

À titre d'exemples voici quelques énoncés dont certains sont des pro­po­si­tion­s, d'autres non pour cette définition :

1. Il pleut,
2. Pourquoi le poulet a-t-il traversé la route ?
3. Ce chapitre est trop long à lire,
4. \(\def\then{{\;\Rightarrow\;}}\def\iff{{\;\Leftrightarrow\;}}1+2=3\),
5. Ce cours sera en ligne le 24 février 3016,
6. L'ensemble des nombres algébriques est dénombrable,
7. Si les poules avaient des dents, alors j'irais sur la lune,
8. À la montagne, on est plus vite en haut qu'à pied.
9. Je mens,
10. \(0\,(\,4=-1\),
11. Cette phrase n'a pas de valeur de vérité,
12. \(1+\sqrt{x} > 4\)
13. Cette phrase n'est pas une phrase.

L'énoncé #2 est une interrogation, l'énoncé #8 est absurde, l'énoncé #10 n'est pas correct syn­ta­xi­que­ment. On ne peut pas attribuer de valeur de vérité à l'énoncé #12 sans connaître la valeur de la variable numérique \(x\), il ne s'agit pas stricto sensu d'une pro­po­si­tion­, on utilise dans ce cas le terme de prédicat ou d'énoncé contingent, qui est le centre d'étude du prochain chapitre.

Tous les autres énoncés sont des pro­po­si­tion­s, mais il n'est pas toujours possible de leur affecter une valeur de vérité sans autres considérations. En effet, la valeur de vérité de la pro­po­si­tion­ #1 dépend implicitement du contexte, le lieu et le moment, tout comme celle de la pro­po­si­tion­ #3 qui dépend du lecteur. Il est donc délicat de les considérer comme des pro­po­si­tions mathématiques stricto sensu. La pro­po­si­tion­ #4 est vraie pour peu que l'on admette les règles de représentation des nombres et que l'on connaisse les rudiments du calcul. Établir une valeur de vérité de la pro­po­si­tion­ #5 est illusoire (ce qui ruine au passage mes espoirs de postérité). La pro­po­si­tion­ #6 demande une certaine connaissance de l'arithmétique pour établir qu'elle est vraie. La pro­po­si­tion­ #7 est vraie du point de vue du logicien, mais peut sembler absurde, voire fausse pour le lecteur lambda. Les pro­po­si­tion­s #9 et #11 sont des paradoxes logiques, elles ne peuvent être vraies ou fausses sans créer une contradiction. Les paradoxes logiques émergent parfois quand il y a autoréférence, c'est-à-dire quand un énoncé fait référence à lui-même* Par exemple la pro­po­si­tion Je suis un men­teur ne peut être vraie ou fausse sans abou­tir à une con­tra­dic­tion. mais cela n'a rien de systématique, par exemple la pro­po­si­tion­ #13 est fausse.

Il apparaît que l'interprétation d'une pro­po­si­tion­ en langue naturelle n'est pas un exercice trivial, loin s'en faut. Toujours dans ce cadre, nous allons voir qu'il est éga­lement délicat d'analyser les énon­cés contenant des con­nec­teurs logiques pourtant omniprésents dans nos langues naturelles. Con­si­dé­rons les phrases suivantes :

1. Le cassis ou le poivre sont des baies.
2. Je travaille ou je me repose.
3. Apprenez votre cours ou vous aurez une mauvaise note.
4. Alice et Bob sont mariés.
5. Les étudiants dont la note en maths est supérieure à 7 et inférieure à 12.
6. Je suis déçu du résultat du contrôle continu et je jette toutes les copies.
7. Le facteur dépose le courrier donc le chien aboie.
8. Il pleut et je dois sortir les poubelles.

Certains con­nec­teurs peuvent avoir une signification différente selon le contexte. Le con­nec­teur ou de la première phrase est inclusif, le second est exclusif et le troisième exprime une conséquence. La quatrième phrase laisse entendre qu'Alice est mariée avec Bob, mais ce n'est pas une cer­ti­tu­de, il est donc difficile de lui attribuer une valeur de vérité. Le con­nec­teur et de l'énoncé #5 code une énu­mé­ra­tion et pas une simple conjonction. De même, la conjonction de l'énoncé #6 induit une con­sé­quen­ce et celle de l'énoncé #8 induit une obligation.

En général les con­nec­teurs logiques des langues n­atu­rel­les ne sont pas vé­ri­fonc­tion­nels. Sup­posons par exemple que la pro­po­si­tion Le facteur dépose le courrier et la pro­po­si­tion le chien aboie soient toutes deux vraies. Si la pro­po­si­tion­ Le facteur dépose le courrier donc le chien aboie est très certainement vraie, la pro­po­si­tion Le chien aboie donc le facteur dépose le courrier est probablement fausse. Ainsi, en logique na­tu­rel­le, d'autres éléments que la valeur de vérité des pro­po­si­tions connectées in­ter­vien­nent pour fixer la valeur de vérité de leur composition. Dans le langage mathématique, les con­nec­teurs doivent être vérifonctionnels. Cette exigence é­lé­men­tai­re peut créer une césure entre la logique na­tu­rel­le et la logique mathématique.

En anticipant un peu sur l'étude des con­nec­teurs logiques, la valeur de vérité d'une pro­po­si­tion contenant le con­nec­teur logique d'imp­li­ca­tion peut suprendre, ainsi la pro­po­si­tion \[({\color{steelblue}1+2=3})\ \then\ {(\color{steelblue}\text{la Terre est ronde}})\] est vraie, alors qu'il n'y a aucun lien de cause à effet entre les deux pro­po­si­tions con­nec­tées qui sont toutes les deux vraies. Pire, la proposition \[ ({\color{steelblue}1+2=0})\ \then\ {(\color{steelblue}\text{la Terre est ronde}}) \] est également vraie, alors que l'expression \(1+2=0\) est fausse (si on considère l'addition des entiers naturels) !

Nous avons déjà constaté que la valeur de vérité d'une pro­po­si­tion n'est pas con­sub­stan­tiel­le à sa struc­tu­re et nous venons de mettre en évidence que les con­nec­teurs logiques dans les énoncés en langue naturelle peuvent être difficiles à interpréter ou impropres à un usage mathématique. La manière la plus efficace de se débarrasser de ces problèmes consiste à éliminer dans un premier temps toute interprétation dans une pro­po­si­tion­, elle devient une construction purement syntaxique. C'est une façon bien commode de procéder, on limite le champ d'investigation de la logique à des entités simples en les détachant de la réalité. C'est ce que nous faisons en permanence en ma­thé­ma­ti­ques. Même pour un simple calcul comme \begin{equation} \label{expr:decimal} 2\times (5+93)=196. \end{equation} On ne se préoccupe ni de sa signification, ni de savoir si \(196\) représente une quantité, le poids d'une table ou la hauteur d'un immeuble, seule l'application correcte de l'addition et de la multiplication dans l'expression abstraite importe. Le distinguo entre la syntaxe et la sé­man­ti­que de l'expression \(196\) est peut-être difficile à percevoir pour le lecteur car la confusion a été volontairement en­tre­nue par les règles de lecture d'un nombre (ici cent-quatre-vingt-seize) où le chiffre le plus significatif est intégré avant les autres afin d'assurer la perception rapide d'une mesure au lieu d'égrener les chif­fres un, neuf, six. On encapsule ainsi forme et fond. C'est la raison exacte de l'apprentissage de la lecture des mots et des nombres, l'objectif est précisément de ne plus avoir à les déchiffrer (toujours cette analogie avec les nombres !) pour en saisir le sens. En remplaçant l'écriture des nombres en base 10 par leur écriture en chiffres ro­mains, on fait res­surgir la séparation entre syn­taxe et sémantique  :

La lecture des 5 chiffres romains CXCVI n'évoque pas mentalement la quantité que nous per­ce­vons sans peine sous forme décimale \(196\), et pourtant les deux représentations codent exactement le mê­me nombre.

La conclusion de cette section est que la logique pro­po­si­tion­nelle en ma­thé­ma­ti­ques est bien plus contrainte que la logique en langue naturelle et ne recouvre qu'une partie de cette dernière. C'est le prix à payer pour la rigueur et lever toute ambiguïté.

Syntaxe du calcul pro­po­si­tion­nel

Concentrons-nous pour le moment sur les aspects lexicaux et syn­ta­xi­ques du langage, nous re­vien­drons sur l'aspect sémantique un peu plus loin. Il faut tout d'abord disposer d'un lexique de sym­bo­les — un alphabet — pour composer une proposition. Ces symboles sont répartis selon quatre catégories :

1. Les constantes \(\top\) et \({\bot}\).
2. Les variables pro­po­si­tion­nelles ou pro­po­si­tion­s atomiques décrites par des symboles d'un alphabet fini. Elles ne peuvent prendre que les deux valeurs \(\top\) ou \({\bot}\).
3. La parenthèse ouvrante \((\) et la parenthèse fermante \()\).
4. Les con­nec­teurs logiques \(\neg\), \(\vee\), \(\wedge\), \(\Rightarrow\), \(\Leftrightarrow\), \(\veebar\), \(\uparrow\), \(\downarrow\).

Passons à la syntaxe. À partir des variables pro­po­si­tion­nelles, on peut créer de nouvelles ex­pres­sions grâce aux con­nec­teurs logiques qui les mettent en relation dans une formule (nous définirons précisément ce terme plus bas).

Si \(q=1\), le connecteur est dit unaire, si \(q=2\), binaire, si \(q=3\) ternaire, etc.

À l'instar de l'expression arithmétique \(2(x+1)+y\) contenant deux variables \(x\) et \(y\), la valeur d'une formule est fonction* dépend des valeurs des variables pro­po­si­tion­nel­les qu'elle con­tient. Les variables pro­po­si­tion­nelles ne pouvant prendre qu'un nombre fini de valeurs (\(\top\) ou \({\bot}\)), un con­nec­teur logique est en­tiè­re­ment caractérisé par les différentes valeurs possibles de l'expression suivant les valeurs des variables qu'il connecte. Notons que l'on ne peut pas caractériser les opérateurs arithmétiques de cette manière, l'addition dans \(\def\Z{{\Bbb Z}}\Z\) par exemple, car l'ensemble des valeurs possibles des variables est infini.

Il n'est pas nécessaire d'étudier l'analyse combinatoire, pour vérifier qu'il y a \(2^q\) com­bi­nai­sons possibles pour les valeurs des \(q\) variables pro­po­si­tion­nel­les d'un con­nec­teur \(q\)-aire, et donc \(2^{2^q}\) façons différentes de définir un con­nec­teur \(q\)-aire. En effet pour chacune des \(2^q\) valeurs possibles du \(q\)-uplet constitué des \(q\) variables, l'expression peut pren­dre \(2\) valeurs distinctes \(\top\) ou \({\bot}\).

Considérons pour commencer les \(2^{2^1}=4\) con­nec­teurs unaires possibles \(\star_i\) regroupés dans la table ci-dessous.

Les con­nec­teurs unaires \(\star_1\) et \(\star_4\) sont constants et l'expression \(\star_2\;P\) prend exactement les mêmes va­leurs que \(P\), le con­nec­teur \(\star_2\) est ainsi l'identité. Le seul con­nec­teur qui ne soit pas trivial est donc \(\star_3\), c'est la négation logique que l'on notera \(\neg\).

Passons aux \(2^{2^2}=16\) con­nec­teurs binaires possibles \(\diamond_j\) et observons ceux qui présentent un intérêt particulier :

Les deux con­nec­teurs binaires \(\diamond_{1}\) et \(\diamond_{16}\) sont constants, les con­nec­teurs \(\diamond_{4}\) et \(\diamond_{13}\) ne dépendent que de la valeur du premier opérande \(P\) et les con­nec­teurs \(\diamond_{6}\) et \(\diamond_{11}\) ne dépendent que de la valeur du deu­xième opérande \(Q\). Ces \(6\) opérateurs ont donc peu d'intérêt, mais il en reste malgré tout 10. Sept d'entre eux sont baptisés car ils sont com­mu­né­ment utilisés en Ma­thé­ma­ti­ques et/ou en Informatique et/ou en Électronique. On a fi­na­le­ment huit con­nec­teurs utiles, un seul connecteur unaire et sept connecteurs binaires, et selon le con­tex­te ou la discipline, on en utilise tout ou partie :

Quand un con­nec­teur est placé avant ses opérandes, on dit qu'il est en notation préfixe, c'est le cas de l'opérateur unaire de négation \(\neg\). Quand un con­nec­teur est placé après ses opé­ran­des, on dit qu'il est en notation postfixe. Par exemple la transposée d'une matrice \(A\) est gé­né­ra­le­ment écrite sous forme postfixe \(A^t\) bien que l'écriture préfixe \({}^t\!A\) soit également très commune. Quand l'opérateur est binaire et qu'il est placé entre les deux opérandes, on dit qu'il est en notation infixe et c'est généralement cette notation qui est employée en logique pro­po­si­tion­nel­le, on écrit donc plus vo­lon­tiers \(P\Rightarrow Q\) que \(P\ Q\ \Rightarrow\), bien que la notation post­fixe soit très utilisée en in­for­ma­ti­que, elle permet en effet de se passer des pa­ren­thè­ses et d'évaluer très facilement une expression (ce point sera étudié en cours d'algorithmique de deuxième année).

On dispose à présent d'une définition formelle d'une proposition. C'est une formule de la logique pro­po­si­tion­nel­le.

Analyse d'une formule

Une expression telle que \begin{equation} \label{eq:ex1} ((P\Rightarrow Q) \wedge (P\vee \neg R)) \end{equation} est suffisamment courte pour qu'une simple lecture suffise à nous convaincre qu'il s'agit bien d'une formule de la logique pro­po­si­tion­nelle. Les exercices que l'on peut traiter à la main en mathématiques dans ce domaine se préoccupent rarement de questions de cette nature, c'est le calcul littéral qui est privilégié. C'est un problème autrement plus ardu en in­for­ma­ti­que car in fine, ce sont des machines qui vont analyser ces expressions et les instances qu'elles doivent être en mesure de traiter ne se limitent pas à une poignée de symboles, elles sont supposées quelconques.

Avant même d'automatiser le processus, problème qui sera abordé en théorie des langages, il faut savoir démontrer qu'une expression est bien formée. Il faut être en mesure de décrire comment elle a été construite à partir des \(5\) règles fournies dans la définition d'une formule. On peut partir du bas avec les atomes et les constantes en construisant successivement de nouvelles formules (analyse ascendante) jusqu'à obtenir la formule souhaitée, ou du haut, en décomposant la formule et en recommençant sur chaque sous-formule (analyse descendante).

Voici une séquence de rè­gles possibles en analyse ascendante. À chaque étape, on définit une nou­vel­le formule qui est exploitée dans la construction des formules suivantes. La règle appliquée est indiquée au-dessus de l'affectation : \begin{align*} f_1&\ {\color{#FF8}\overset{R_1}{\leftarrow}}\ P\\ f_2&\ {\color{#FF8}\overset{R_1}{\leftarrow}}\ Q\\ f_3&\ {\color{#FF8}\overset{R_5}{\leftarrow}}\ (f_1\then f_2)\\ f_4&\ {\color{#FF8}\overset{R_1}{\leftarrow}}\ R\\ f_5&\ {\color{#FF8}\overset{R_4}{\leftarrow}}\ \neg f_4\\ f_6&\ {\color{#FF8}\overset{R_5}{\leftarrow}}\ (f_1\vee f_5)\\ f_7&\ {\color{#FF8}\overset{R_5}{\leftarrow}}\ (f_3\wedge f_6)\\ \end{align*}

Voici une séquence de rè­gles possible en analyse descendante. À chaque étape, un cadre nu­mé­ro­té indique la règle qui décompose la sous-formule : \begin{align*} &\boxed{{\color{#FFF}formule}}_{\;5}\\ (\boxed{{\color{#FFF}formule}}_{\;5}&\wedge{\color{#FFF}formule})\\ (({\boxed{{\color{#FFF}formule}}}_{\;1} \Rightarrow{\color{#FFF}formule})&\wedge{\color{#FFF}formule})\\ ((P \Rightarrow {\boxed{{\color{#FFF}formule}}_{\;1}})&\wedge {\color{#FFF}formule})\\ ((P \Rightarrow Q)&\wedge {\boxed{{\color{#FFF}formule}}_{\;5}})\\ ((P \Rightarrow Q)&\wedge ({\boxed{{\color{#FFF}formule}}_{\;1}}\vee{\color{#FFF}formule}))\\ ((P \Rightarrow Q)&\wedge (P\vee {\boxed{{\color{#FFF}formule}}_{\;4}}))\\ ((P \Rightarrow Q)&\wedge (P\vee \neg {\boxed{{\color{#FFF}formule}}_{\;1}}))\\ ((P \Rightarrow Q)&\wedge (P\vee \neg R)) \end{align*}

Sauf cas particuliers, il existe plusieurs séquences de règles possibles pour établir une formule. Une telle séquence de règles s'appelle une dérivation de la formule. La re­pré­sen­ta­tion d'une formule à l'aide d'un arbre de dérivation (ou arbre syntaxique) permet de mieux comprendre sa structure. C'est un arbre schématisé dont le principe de construction est simple et inductif. Une formule avec un con­nec­teur \(q\)-aire est représentée à l'aide de \(q+1\) nœuds dans cet arbre, le con­nec­teur est placé à la racine de l'arbre qui est reliée à chacun des \(q\) opérandes dans l'ordre de leur apparition dans la formule.

Les deux arbres suivants représentent res­pec­ti­ve­ment une formule avec un con­nec­teur unaire \(\star\) et son opérande et une formule avec un con­nec­teur binaire \(\square\) et ses deux opérandes (les arbres sont dits unai­re et binaire) :

          

Si une formule peut admettre plusieurs dérivations, elle n'a qu'un seul arbre de dérivation, ce qui justifie l'emp­loi du singulier défini. Comme pour les opérations arithmétiques, on décide de certaines prio­ri­tés pour simp­li­fier les écri­tu­res. La négation est prioritaire sur la conjonction qui est prioritaire sur la disjonction, elle-mê­me prioritaire sur l'implication. Néanmoins, il est hautement pré­fé­ra­ble d'écrire toutes les pa­ren­thè­ses, l'expérience prouve qu'elles facilitent beaucoup plus sou­vent la lecture qu'elles ne la com­pli­quent. On simplifie malgré tout les formules en omettant les parenthèses aux extrémités, la formule simplifiée de \((\ref{eq:ex1})\) s'écrit \((P\Rightarrow Q) \wedge (P\vee \neg R).\)

Un étudiant s'étonnait de ne pas avoir eu le point attribué à une ques­tion dans laquelle il fallait représenter l'arbre de dérivation de la formule \(\neg P\Rightarrow Q\) (à droite ci-dessous) qu'il avait représenté comme à gauche ci-dessous en arguant qu'ils étaient égaux :

au lieu de

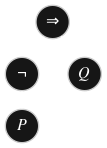
Effectivement, dans ces deux graphes, les relations entre éléments matérialisées par des arcs sont strictement égales (vous pourrez en faire la preuve à titre d'exercice en définissant l'ensemble sur lequel sont définis les graphes de ces deux relations une fois cette partie du cours étudiée)^* ils le sont éga­le­ment du point de vue to­po­lo­gi­que.. Néanmoins, il s'agit ici d'une représentation avec une sémantique, elle met en particulier en évidence la position des opérandes gauche et droit de part et d'autre d'un opérateur binaire comme l'implication \(\Rightarrow\). Autrement dit, la représentation à gauche ne fournit pas la même information que celle de droite compte tenu des conventions de représentation des arbres de dérivation. Je doute échapper à une contravention pour conduite à contresens en prétextant que les deux pan­neaux à sens unique ⬆ et ⬇ sont égaux…

Analogie avec un langage de programmation

Comme nous l'avons précisé en introduction, les mathématiques s'expriment grâce à un empilement de langages, celui de la logique pro­po­si­tion­nel­le étant le premier et le plus simple d'entre eux. On retrouve cette hiérarchie dans les langages de programmation eux même empilement de plusieurs langages et la logique pro­po­si­tion­nel­le en fait généralement partie, comme c'est le cas en Python.

Bien sûr, l'écriture des programmes in­for­ma­ti­ques passant par l'usage d'un clavier avec un alphabet restreint, le lexique du langage de la logique pro­po­si­tion­nel­le est différent de celui des mathématiques et les symboles représentant les connecteurs logiques sont souvent codés par leurs noms en toutes lettres, or pour \(\vee\), and pour \(\wedge\), etc. Au même titre que le langage de la logique pro­po­si­tion­nel­le est un sous-langage du langage mathématique, c'est également un sous-langage du Python.

Par exemple dans la formule \(P\vee (Q\wedge R)\), les variables pro­po­si­tion­nel­les \(P\), \(Q\) et \(R\) sont codées en Python par les trois objets de type booléen P, Q et R et la formule homologue est P or (Q and P).

Ce n'est pas le seul sous-langage mathématique qui a été transposé en Python, celui de l'arithmétique l'a été également avec quelques bouleversements mineurs sur le lexique et la syntaxe pour les mêmes raisons de limitation du clavier. La multiplication \(\times\) est codée par le symbole * par exemple.

Sémantique du calcul pro­po­si­tion­nel

Interprétation d'une formule

Revenons à la sémantique. Il s'agit d'attribuer un sens à une formule, on veut l'interpréter. Seules deux valeurs logiques sont possibles, vrai ou faux, c'est la valeur de vérité de la formule. Une in­ter­pré­ta­tion est donc une application \(I:{\mathscr F}\rightarrow \{vrai,\;faux\}\) de l'en­semb­le des formules pro­posi­tion­nel­les \(\mathscr F\) dans l'ensemble* Les termes ensemble et application ne sont pas dé­fi­nis for­mel­le­ment à ce stade mais la vision naïve est suf­fi­san­te ici. \(\{vrai,\;faux\}.\)

Les règles qui permettent d'attribuer un sens aux formules doivent être cohérentes avec les règles de construction syntaxique. La fonction d'in­ter­pré­ta­tion \(I\) est définie en fixant arbi­trai­re­ment une valeur de vérité \(vrai\) ou \(faux\) à chacune des variables pro­po­si­tion­nelles. C'est la seule marge de manœuvre dont on dispose si l'on décide que les constantes \(\top\) et \(\bot\) (objets syntaxiques) sont in­ter­pré­tées res­pec­ti­ve­ment comme les valeurs logiques \(vrai\) et \(faux\) (objets sé­man­ti­ques), c'est-à-dire \(I(\top):=vrai\) et \(I(\bot):=faux\) et que la fonc­tion d'interprétation d'une formule se conforme aux tables de vérité des con­nec­teurs logiques. Ainsi pour respecter la cohérence entre syntaxe et sémantique, l'interprétation des différentes variables pro­po­si­tion­nel­les qui sont impliquées dans une formule fixe l'interprétation de la formule.

Une formule de la logique pro­po­si­tion­nelle est bien une pro­po­si­tion au sens de cette définition informelle. Nous pouvons donc employer le terme pro­po­si­tion pour désigner une formule de la logique pro­po­si­tion­nelle.

En remplaçant \(\top\) par \(vrai\) et \(\bot\) par faux dans les tables des con­nec­teurs logiques, on obtient leurs tables de vérité. Nous avons regroupé les 7 tables de vérité des con­nec­teurs logiques binaires dans un unique tableau et avons résumé les valeurs de vérité vrai et faux par \(V\) et \(F\) respectivement pour plus de lisibilité.

La table de vérité d'une formule contient ses valeurs de vérité pour toutes les combinaisons possibles des variables pro­po­si­tion­nel­les qu'elle contient. La table de vérité de la formule \(((P\Rightarrow Q) \wedge (P\vee \neg R))\) est donnée ci-dessous et pour faciliter la comp­ré­hen­sion, les deux sous-formules de cette conjonction y sont pré­sen­tes également :

Comment construit-on effectivement une table de vérité ? L'algorithme est simple, on se donne tout d'abord une in­ter­pré­ta­tion \(\color{#AA88FF}{I}\) pour remplacer chaque variable pro­po­si­tion­nelle \(P\) — donc chaque feuille de l'arbre de dérivation (sur fond gris dans les exemples) — par sa valeur de vérité \(I(P)\), puis on ap­pli­que in­duc­ti­ve­ment les deux opérations sui­vantes sur l'arbre de dérivation :

1. On remplace chaque sous-arbre constitué d'un con­nec­teur unaire de négation et de sa feuille par un seul nœud contenant la négation de la constante contenue dans la feuille.
2. On remplace chaque sous-arbre constitué d'un con­nec­teur binaire et de ses deux feuilles par un seul nœud contenant l'interprétation de la sous-formule correspondante.

Évaluation de l'arbre de dérivation de la formule propositionnelle \((P\Rightarrow Q)\wedge( P\vee\neg R)\) pour l'interprétation \(I\).

Équivalence logique des formules

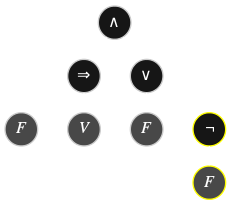
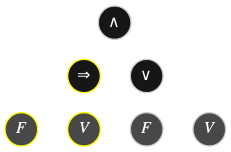
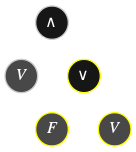
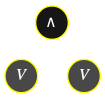
Des formules différentes de la logique propositionnelle peuvent avoir une table de vérité identique, de la même manière que deux expressions différentes de l'arithmétique peuvent être égales : \(x(2+y)=2x+xy\).

On montre aisément que pour toute proposition \(P\), on a \begin{equation}\label{eq:neg} \neg(\neg P)\ \equiv\ P \end{equation} et que deux propositions \(P\) et \(Q\) peuvent être échangées sans rien changer aux tables de vérités des formules \(P \vee Q\) et \(P\wedge Q\), au­tre­ment dit que les con­nec­teurs logiques de dis­jonc­tion et de conjonction sont com­mu­ta­tifs : \begin{align}\label{eq:comou} P \vee Q\ &\equiv\ Q\vee P\\ P \wedge Q\ &\equiv Q\wedge P\label{eq:comet} \end{align}

D'autre part, on a les deux équivalences logiques suivantes, qui sont souvent utilisées en ma­thé­ma­ti­ques pour définir les con­nec­teurs d'implication et d'équivalence à partir des trois con­nec­teurs de né­ga­tion, de conjonction et de disjonction : \begin{align}\label{eq:implique} P\Rightarrow Q&\ \equiv\ \neg{P}\vee Q\\ P\Leftrightarrow Q&\ \equiv\ (P\Rightarrow Q) \wedge (Q\Rightarrow P)\label{eq:eq} \end{align}

Nous verrons plus bas que le con­nec­teur d'implication \(\Rightarrow\) n'est pas commutatif, alors que la com­mu­ta­ti­vi­té du con­nec­teur \(\wedge\) entraîne celle du con­nec­teur \(\Leftrightarrow\) d'équivalence.

On peut se demander pourquoi nous n'avons pas étudié d'autres opérateurs que les opé­ra­teurs unaires et bi­nai­res ? Le théorème suivant et son corollaire four­nis­sent une jus­ti­fi­ca­tion.

Nous verrons au chapitre sur le calcul booléen que l'on peut obtenir un résultat plus fort encore et que l'on peut se contenter d'un unique opérateur binaire. Mais le mathématicien savait déjà que l'on pouvait se contenter des trois con­nec­teurs \(\neg\), \(\wedge\) et \(\vee\) pour tout exprimer.

Déduction et connecteur d'implication

Nous allons étudier de plus près le connecteur logique d'implication (\(\then\)) et expliciter son rôle dans les mécanismes déductifs en mathématiques.

Observons attentivement la table de vérité de ce connecteur logique :

Comme on peut le constater, si la proposition \(P\then Q\) est vraie, cela ne nous donne aucune d'information sur la valeur de vérité de la proposition \(P\) ni de la proposition \(Q\). En effet, si \(P\then Q\) est vraie, \(P\) est fausse dans l'interprétation \(1\) et \(2\) mais vraie dans l'interprétation \(4\), et \(Q\) est fausse dans l'interprétation \(1\) mais vraie dans l'interprétation \(2\) et \(4\) :

Pour démontrer qu'une proposition du type \(P\then Q\) est vraie, il suffit de vérifier que si \(P\) est vraie alors \(Q\) n'est pas fausse pour éliminer l'interprétation \(3\) de la table. Dans les \(3\) autres cas, il n'y a rien à faire, \(P\then Q\) est toujours vraie.

Plus troublant, la proposition \((0=1)\Rightarrow (3\ \text{est pair})\) est vraie. Le mot implication dans la langue naturelle induit une relation de cause à effet entre \(P\) et \(Q\) que l'on interprète comme une déduction, ce que ne dit pas l'assertion \(P\Rightarrow Q\). Les con­nec­teurs logiques établissent des liens de corrélation entre les propositions \(P\) et \(Q\) et non des liens de causalité. Ce sont de bonnes raisons pour ne pas interpréter le symbole \(\Rightarrow\) comme le mot donc en français. Rappelons que \((P\then Q)\equiv(\neg P\vee Q)\), ainsi la proposition \((0=1)\Rightarrow (3\ \text{est pair})\) est logiquement équivalente à la proposition \((0\not=1)\vee (3\ \text{est pair})\), ce qui est déjà moins troublant.

Ceci nous amène à nous interroger légitimement sur le choix du mot implication pour qualifier ce con­nec­teur logique, puisqu'il a sans conteste un sens déductif en français. Continuons nos investigations.

On peut se convaincre que le con­nec­teur d'implication tel qu'il est défini en logique pro­po­si­tion­nelle est le meilleur choix parmi les 16 con­nec­teurs logiques binaires pour approximer son homologue en langue naturelle. En effet, la valeur de vérité de l'implication \(P\then Q\) ne peut pas dépendre exclusivement de \(P\), ni exclusivement de \(Q\) et le con­nec­teur n'est manifestement pas commutatif, il ne reste alors que les con­nec­teurs \(\diamond_3\), \(\diamond_5\), \(\diamond_{12}\) ou \(\diamond_{14}\) et uniquement \(\diamond_{14}\) si l'on admet que si \(P\) est vrai \(P\then Q\) doit avoir la valeur de \(Q.\)

Revenons à la table de vérité de l'implication. On observe que si \(P\then Q\) est vraie et que \(P\) l'est également, alors nécessairement la proposition \(Q\) est vraie. La règle ci-dessous décrit le rôle de la pro­po­si­tion \(P\Rightarrow Q\) dans le processus déductif et donne un sens précis aux mots donc ou alors dans le discours ma­thé­ma­ti­que. La déduction logique est symbolisée par le signe \(\vdash\) (ou \(\therefore\)) séparant les prémisses (ou hypothèses) \(P\) et \(P\Rightarrow Q\), du conséquent (ou conclusion) \(Q\).

Ces notations sont largement utilisées dans l'étude des systèmes de décision, des logiques non clas­si­ques, en théorie de la dé­mons­tra­tion, en intelligence artificielle, etc.

La pro­po­si­tion­ \(Q\Rightarrow P\) est appelée implication réciproque de l'implication \(P\Rightarrow Q\). Ce n'est pas sa né­ga­tion, en effet

Pour vérifier une équi­va­len­ce, d'après la définition \((\ref{eq:eq})\) il faut démontrer les deux imp­li­ca­tions \(P\Rightarrow Q\) et \(Q\Rightarrow P\), autrement dit que \(P\) est une condition nécessaire et suffisante de \(Q\) (ou réciproquement), ce que l'on énonce souvent en disant \(P\) si et seulement si \(Q\).

Il est aisé de vérifier les deux équivalences logiques qui suivent en construisant les tables de vérités des assertions qui les constituent et qui portent le nom du mathématicien* Augustus De Morgan était un ma­thé­ma­ti­cien bri­tan­ni­que du 19^ème siè­cle. qui les a énoncées.

L'antilogie la plus simple est bien sûr \(P\wedge\neg P\).

On cherche bien sûr à éviter les théories mathématiques qui contiennent des paradoxes.

Les trois tautologies suivantes sont très utilisées pour construire des démonstrations mathématiques :

− La non contradiction : \(\neg(P\wedge \neg P)\)

− Le tiers exclu : \(P\vee \neg P,\)

− L'analyse de cas : \((P\then Q)\wedge(\neg P\then Q)\iff Q,\)

La non contradiction \(\neg(P\wedge \neg P)\) exprime qu'une proposition et sa négation ne peuvent être vraies simultanément, on ne veut pas de paradoxes. Elle permet d'élaborer une stratégie de démonstration dite dé­mons­tra­tion par l'absurde. Plutôt que de montrer qu'une pro­po­si­tion \(P\) est vraie, on suppose qu'elle est fausse pour en déduire la contradiction \(P\wedge \neg P\) invalidant l'hypothèse et permettant de conclure que \(P\) est vraie grâce au tiers exclu. Ainsi un inspecteur qui suppose qu'un cambrioleur est passé par une fenêtre et après investigation, ne trouve aucune trace d'effraction sur cette fenêtre, conclura que son hypothèse était absurde et en déduira que le cambrioleur est entré par un autre moyen.

Le tiers exclu \(\neg(P\vee \neg P)\) exprime qu'une pro­po­si­tion­ ou sa négation doit être vraie, autrement dit que l'on exclut une troisième possibilité*. La logique in­tui­tion­nis­te rejette le tiers exc­lu et par conséquent le rai­son­ne­ment par l'ab­sur­de. Notons que la non contradiction et le tiers exclu sont la négation l'une de l'autre d'après les lois de De Morgan \((\ref{eq:morganou})\) et \((\ref{eq:morganet})\). La troisième exprime le fait que c'est l'in­ter­pré­ta­tion de \(Q\) qui fixe la valeur de vérité de la conjonction, quelle que soit l'interprétation de \(P\).

L'analyse de cas \((P\then Q)\wedge(\neg P\then Q)\iff Q\) exprime le fait que \(P\) soit vrai ou non, \(Q\) est vrai.

Propriétés des con­nec­teurs logiques

En guise de référence rapide, on regroupe ici les propriétés les plus importantes des con­nec­teurs lo­gi­ques. Soit \(P\), \(Q\) et \(R\) des pro­po­si­tions. Alors

Commutativité de \(\wedge\) et \(\vee\) : \( (P\wedge Q)\equiv (Q\wedge P)\ \text{et}\ (P\vee Q)\equiv (Q\vee P). \)

Associativité de \(\wedge\) et \(\vee\) : \( ((P\wedge Q)\wedge R)\equiv (P\wedge(Q\wedge R))\ \text{et}\ ((P\vee Q)\vee R)\equiv (P\vee(Q\vee R)). \)

Idempotence de \(\wedge\) et \(\vee\) : \( (P\wedge P)\equiv P\ \text{et}\ (P\vee P)\equiv P. \)

Lois de De Morgan : \( \neg(P\wedge Q)\equiv (\neg P\vee\neg Q)\ \text{et}\ \neg(P\vee Q)\equiv (\neg P\wedge\neg Q) \)

Distributivité : \( (P\wedge(Q\vee R))\equiv ((P\wedge Q)\vee (P\wedge R))\ \text{et}\ (P\vee(Q\wedge R))\equiv ((P\vee Q)\wedge (P\vee R)). \)

Absorption : \( (P\wedge(P\vee Q))\equiv P\ \text{et}\ (P\vee(P\wedge Q))\equiv P. \)

Éléments neutres : \( (P\wedge V)\equiv P\ \text{et}\ (P\vee F)\equiv P. \)

Éléments absorbants : \( (P\vee V)\equiv V\ \text{et}\ (P\wedge F)\equiv F. \)

Transitivité de l'implication : \( ((P\then Q)\wedge(Q\then R))\then(P\then R). \)

Formalisation des problèmes et raisonnement

Les robots

Nous pouvons à présent étudier le problème de robots que nous avons présenté en introduction. On rappelle qu'un robot en bon état fait toujours un bon diagnostic et qu'un robot défectueux fait toujours un mauvais diagnostic. Les trois robots font les affirmations suivantes :

On introduit les variables pro­po­si­tion­nelles \(\color{#FF8}X\), \(\color{#F44}B\) et \(\color{#88F}A\) définies par

• \(\color{#FF8}X:\) xam est en bon état (il fait donc un bon diagnostic),
• \(\color{#F44}A:\) arg est en bon état (il fait donc un bon diagnostic),
• \(\color{#88F}B:\) bax est en bon état (il fait donc un bon diagnostic).

Si l'on observe la table de vérité du con­nec­teur d'équivalence \(\iff\), on note que \(P\iff Q\) est vrai si et seulement si les deux variables \(P\) et \(Q\) ont la même valeur de vérité, c'est-à-dire si les deux sont vraies ou si les deux sont fausses (on en déduit au passage que \((P\iff Q)\equiv(P\wedge Q)\vee (\neg P\wedge\neg Q)\)). On formalise alors les pro­po­si­tions de xam, arg et bax respectivement par :

1. \({\color{#FF8}P_X}:\) \((A\iff B)\),
2. \({\color{#F44}P_A}:\) \(\neg B\),
3. \({\color{#88F}P_B}:\) \((X\wedge A)\).

Il faut également traduire l'hypothèse qui dit qu'un robot en bon état fait toujours un bon diagnostic et qu'un robot défectueux fait toujours un mauvais diagnostic. Autrement dit, les pro­po­si­tions \(X\) (resp. \(A\) et \(B\)) et \(P_X\) (resp. \(P_A\) et \(P_B\)) ont la même valeur de vérité, ce qui se traduit par la formule \begin{equation} \label{formrobot} {\mathscr F}:=({\color{#FF8}P_X}\iff {\color{#FF8}X})\wedge({\color{#F44}P_A}\iff {\color{#F44}A})\wedge({\color{#88F}P_B}\iff {\color{#88F}B}). \end{equation}

On construit ensuite la table de vérité des trois pro­po­si­tions \({\color{#FF8}P_X}\), \({\color{#F44}P_A}\) et \({\color{#88F}P_B}\), puis celle de la formule \(\mathscr F\) :

Comme on peut le constater, seule l'interprétation 3 satisfait la formule \((\ref{formrobot})\), il faut donc réparer xam et bax.

Le logicien amoureux

Traitons un deuxième exemple. On interroge un logicien, qui dit toujours la vérité, sur sa vie sen­ti­men­ta­le et il affirme :

• (a) J'aime Marie ou j'aime Anne.
• (b) Si j'aime Marie, alors j'aime Anne.

On peut traduire ces deux as­ser­tions en formules pro­po­si­tion­nelles. Pour cela on définit les variables pro­po­si­tion­nel­les \(A\) et \(M\) qui sont interprétées de la manière suivante :

• \(A:\) J'aime Anne,
• \(M:\) J'aime Marie,

La pro­po­si­tion (a) se traduit par \(M\vee A\) et la pro­po­si­tion (b) par \(M\then A\). On construit leurs tables de vérité :

Les deux dernières lignes de cette table de vérité (les seules qui assurent que les assertions du logicien sont vraies) montrent que le logicien aime nécessairement Anne mais on ne sait rien de plus au sujet de la nature de sa relation avec Marie. Il nous faut donc un complément d'information pour conclure. À la question Est-il vrai que si vous aimez Marie, alors vous aimez Anne ?, le logicien répond*Notez que cette de­man­de de con­fir­ma­tion de (b) était en soi inu­ti­le puis­que le lo­gi­cien dit tou­jours la vé­ri­té.

• (c) Si c'est vrai, alors j'aime Marie,
• (d) Si j'aime Marie, alors c'est vrai.

Si on traduit ces deux dernières affirmations en pro­po­si­tions, on obtient \((M\then A)\then M\) pour (c) et \(M \then (M\then A)\) pour (d) et on reconnaît là l'équivalence \((M\then A)\iff M\) que l'on rajoute dans la table de vérité. Cette fois il ne reste qu'une seule interprétation pro­po­si­tion­nelle de \(A\) et \(M\) qui assure la vérité des trois pro­po­si­tions, celle où le logicien aime les deux femmes :

Les différentes assertions du logicien ont donc été traduites sous formes de pro­po­si­tions et nous avons cherché les interprétations \(I\) des différentes variables assurant que leur conjonction était vraie, ici \(I(A)=V\) et \(I(M)=V\).

Limites de la logique pro­po­si­tionnelle

De manière générale, un énoncé peut très bien aboutir à la formalisation d'une pro­po­si­tion avec plusieurs in­ter­pré­ta­tions valides (si elles le sont toutes, c'est une tautologie) ou au­cu­ne (antilogie). Ceci justifie la définition suivante :

On utilise la même terminologie pour un ensemble de formules pour signifier que c'est leur con­jonc­tion qui est satisfaisable ou non.

Déterminer si une formule est satisfaisable est un problème extrêmement difficile. Les scientifiques pensent, dans leur grande majorité, qu'aucun moy­en efficace ne permet d'y répondre en toute généralité (cette question sera abordée en détail en master.) On peut, bien sûr, construire la table de vérité de la formule pour faire cette vérification, mais c'est un travail qui devient littéralement infaisable, même pour un ordinateur, dès qu'il y a plus de quelques dizaines de variables pro­po­si­tion­nelles dans la formule.

Les exemples de formalisation que nous venons de traiter illustrent les limites de la logique pro­po­si­tion­nel­le. Son manque d'expressivité nous a contraint à créer un grand nombre de variables pour décrire les différents cas.

D'autre part, nombre d'énoncés et de raisonnements logiques en langue naturelle ne sont pas trans­po­sab­les en formules de la logique pro­po­si­tion­nel­le, par exemple Tout étudiant·e en licence d'in­for­ma­ti­que suit le cours de mathématiques, Alice est étudiante en licence d'in­for­ma­ti­que donc Alice suit le cours de mathématiques. Les relations entre objets ne peuvent pas être exprimées, seuls des faits isolés sont modélisables, si Idris est l'ami de Sacha et Bob est l'ami d'Alice, ces deux propositions ne donnent aucun statut à la relation d'amitié sous-jacente pourtant manifeste, ne serait-ce que syntaxiquement.

Mais pire encore, que se passerait-il si un problème faisait référence aux entiers naturels ? Par exemple, si l'on évoquait dans un énoncé une combinaison codée par un nombre de taille arbitraire ? Manipuler un très grand nombre de variables pro­po­si­tionnelles, voire une infinité de variables pro­po­si­tion­nel­les, n'est envisageable ni pour un être humain, ni pour une machine. Il faut pouvoir décrire une infinité de situations à l'aide d'une description finie, c'est ce que permet de faire la logique des prédicats.

L'apport de la logique des prédicats permet également de formaliser des situations finies de manière bien plus concise que la logique propositionnelle, on exprime par exemple qu'une partie \(X=\{x_1,x_2,\ldots,x_n\}\) de \(\N\) ne contient que des entiers pairs par l'expression formelle \[ \forall x\in X\ \ \exists k\in\N\ \ x=2\, k. \] plutôt que par la conjonctions des \(n\) pro­po­si­tions \[ x_1\ \text{est pair}\ \text{et}\ x_2\ \text{est pair}\ \text{et}\ x_3\ \text{est pair},\ldots,\ \text{et}\ x_n\ \text{est pair}. \]

Le prochain chapitre est consacré à l'étude de la logique des prédicats dans le cadre de la théorie des ensembles de Zermelo-Fraenkel (abrégée en théorie zf).

[(False,False),(False,True),(True,False),(True,True)]

[(False,False,False),(False,True,False),(True,False,False),(True,True,True)]

[(True,False)]