 |
Évolution des techniques de reproduction sonore
Les premiers enregistrements sonores datent du milieu du dix-neuvième siècle avec l'invention du Phonographe par Thomas Edison. Pourtant la qualité de reproduction des différents supports employés reste très peu satisfaisante jusque dans les années quarante. La première réelle évolution provient de l'invention du microsillon en 1948. La seconde, et sûrement une des plus magistrale, est la stéréophonie. Ce procédé consiste à transcrire, non plus un signal sonore, mais deux, un gauche et un droit, de manière à restituer une sensation d'espace. Il faut remarquer à ce sujet que la stéréophonie ne cadre qu'imparfaitement avec notre perception binaurale du son. En effet, nos oreilles enregistrent un signal provenant de toutes les directions, et le cerveau situe les différentes sources sonores grâce aux différences de perception entre les deux oreilles, de la même façon que nous voyons en relief grâce à nos deux yeux. La stéréophonie n'est donc qu'une approximation satisfaisante de notre écoute.D'autres systèmes ont été étudiés, par exemple la quadriphonie où l'auditeur est placé au centre d'un carré formé par quatre sources sonores. Cette technique très à la mode dans les années 70, fut abandonnée pour des raisons commerciales, mais l'idée d'utiliser plus de deux sources sonores revient aujourd'hui sous une forme beaucoup plus évoluée et surtout beaucoup plus réaliste, les processeurs d'ambiance comme le DSP 1000 de Yamaha. On ne se contente plus des deux signaux gauche et droit, mais on rajoute d'autres sources sonores dites de présence : une centrale entre les deux sources traditionnelles et deux à l'arrière (voir figure 1). Le processeur additionne un message d'ambiance distinct à chacun des canaux traditionnels et envoie dans ces satellites un message qui lui est propre. Ces signaux d'ambiance ont été obtenus par une simulation des échos et réverbérations du signal stéréophonique dans un milieu choisi par l'auditeur, par exemple une cathédrale, un auditorium, une salle de concert ou plus simplement une boite de jazz. La simulation est réalisée à partir de nombreux paramètres relevés dans un environnement réel et numérisés.
 |
Ce système a un énorme avantage par rapport à la quadriphonie : il n'est plus nécessaire d'enregistrer quatre signaux, on se contente du signal stéréophonique obtenu avec n'importe quel appareil. De plus il s'avère que le résultat est très réaliste et le prix de ces appareils est devenu ``abordable'', il avoisine les 10000 francs avec l'amplificateur. Une autre grande évolution dans le stockage des informations audio fut l'enregistrement sur bandes magnétiques. Cette technique qui s'est très rapidement généralisée a permis d'améliorer considérablement la qualité des enregistrements (analogiques). Elle est toujours en vigueur et atteint aisément la qualité des enregistrements numériques, mais pas leur souplesse de traitement.
Les techniques d'enregistrement numérique datent du début des années 70 alors que l'idée de A.H. Reeves de numériser le signal audio (la Pulse Code Modulation) date de 1937! Un des tout premiers enregistrements numériques (1974) fut japonais, l'intégrale des sonates de Mozart interprétées par M.J. Pires. Pour les européens ce fut le Fidelio de Beethoven par G. Solti. La firme hollandaise Philips et la firme japonaise Sony étudièrent parallèlement dès 1974 la possibilité de stocker des informations numériques sur un support à lecture optique. Leurs recherches aboutirent sensiblement au même moment, au début des années 80. Pour éviter les problèmes commerciaux que connurent les magnétoscopes à cause des différents standards utilisés (Betamax, V2000, VHS), les deux sociétés s'associèrent pour créer un standard unique connu sous le nom de disque compact, ou C.D. pour les intimes.
La grande différence entre le disque compact et les autres supports n'est pas tant l'amélioration de la qualité sonore que la façon radicalement novatrice de gérer l'information. En effet les hautes performances du disque compact étaient déjà atteintes grâce aux bandes magnétiques, mais sur des appareils sophistiqués associés à des sytèmes réducteurs de bruit très onéreux (Dolby, D.B.X. etc...), donc hors de portée du grand public. De plus ces performances ne sont réellement mises en valeur qu'avec un matériel idoine, que ce soit au niveau de l'amplification du signal ou de sa reconstitution physique par des haut-parleurs. Chaque paramètre du son est systématiquement aligné sur le plus mauvais de tous les maillons de la chaîne (bande passante, dynamique, rapport signal/bruit, séparation des canaux, linéarité, distorsion). Cela réserve donc les qualités réelles du disque compact aux amateurs ``éclairés'' ou fortunés.
Comme toutes les révolutions, celle du C.D. ne s'est pas faite sans mal, il fallait surmonter non seulement les formidables problèmes techniques, mais aussi la méfiance des audiophiles, toujours aussi difficiles à convaincre du bien fondé des évolutions technologiques. Comme pour l'avènement de la stéréophonie, longtemps décriée, les critiques furent nombreuses (et parfois justifiées), par exemple sur le son trop ``métallique'' du disque compact ou sur le manque de fluidité des phrases musicales.
Rappels d'acoustique et performances du CD.
Nous allons expliquer à quoi correspondent certaines mesures que l'on voit souvent dans les caractéristiques techniques des appareils de reproduction sonore. Pour cela il est nécessaire de rappeler quelques notions élémentaires d'acoustique (voir [4]).
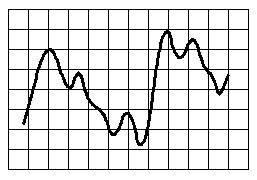
Notre oreille est sensible aux ondes sonores, autrement dit aux effets alternés de dépression et de surpression de l'air qui nous entoure. On récupère ces variations de pression sous forme électrique à l'aide d'un microphone. Très schématiquement, une pastille sphérique est solidaire d'un aimant mobile à l'intérieur d'une bobine. Cette pastille est sensible aux variations de pression acoustique, elle se déplace donc avec l'aimant sur l'axe de la bobine. On a ainsi un courant induit que l'on récupère aux bornes de la bobine (figure 2). On peut alors caractériser un son par une courbe amplitude/temps (figure 3).
 |
 |
Une oreille en parfait état ne perçoit que les sons dont la fréquence est comprise entre 20Hz et 20000Hz, mais l'étendue de cet intervalle décroit rapidement avec l'âge. On appelle souvent cet intervalle la bande audio.
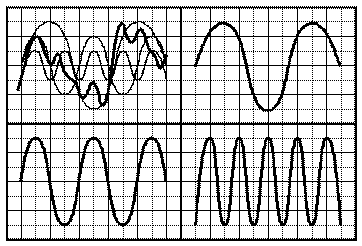
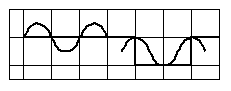
Le la du diapason oscille à une fréquence de 440Hz, on devrait donc obtenir une sinusoïde (cadre supérieur droit de la figure 4), pourtant c'est une courbe plus perturbée que l'on obtient (courbe en gras supérieure gauche de la figure 4). En fait il n'y a pas que le signal à 440Hz qui est émis. En plus de ce signal, dont la fréquence est appelée fréquence fondamentale, il existe toute une série de signaux dont la fréquence est un multiple de la fréquence fondamentale. Ces signaux sont appelés les harmoniques, et on précise le multiple de la fréquence fondamentale, ainsi la fréquence de l'harmonique 2 est égale à 2 fois la fréquence de la fondamentale (cadre inférieur gauche de la figure 4). L'écart entre deux harmoniques consécutives s'appelle une octave1 L'amplitude de chaque harmonique dépend de l'instrument qui génère le son. On reçoit donc la somme de tous ces signaux avec leurs amplitudes respectives (cadre suprieur gauche de la figure 4), ainsi la courbe du la est obtenue en additionnant les harmoniques à la fondamentale (courbes de la figure 4 supérieure gauche, somme en gras).
 |
La suite (le spectre) formée par les amplitudes des harmoniques successives d'un son détermine ce que l'on appelle le timbre, qui caractérise chaque instrument de musique. C'est pour cela que le la d'un piano est différent du la d'une flûte, pour la même fréquence fondamentale. Le signal du la 440 est donc la somme de la série (convergente) des harmoniques qui le compose, cette décomposition est appelée décomposition en série de Fourier du signal. Notre perception du son n'est pas proportionnelle à son intensité mais au logarithme en base 10 de cette intensité. Ainsi on utilise une unité plus pratique, le décibel (dB) :
où I0 désigne une intensité acoustique de référence correspondant au seuil de sensibilité de notre oreille. On peut maintenant décrire quelques paramètres importants en haute fidélité.
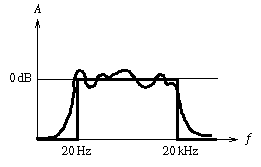
La réponse en fréquence : On peut mesurer sur un appareil de reproduction sonore (analogique ou numérique) les intensités des différentes fréquences de la bande audio qu'il restitue en sortie (fréquences de même intensité en entrée). Un appareil de haute fidélité ne devrait en aucun cas en privilégier certaines, ainsi la courbe amplitude/fréquence devrait ressembler à un rectangle. Ce n'est jamais le cas, en fait on a généralement un plateau plus ou moins bosselé (figure 5), on précise donc très souvent les écarts positifs et négatifs d'amplitude les plus importants par rapport à la moyenne. Le disque compact a une réponse en fréquence comprise entre 20Hz et 20000Hz à +0.5/-1dB.
Remarque : Parfois certains appareils comme les amplificateurs (haut de gamme) annoncent une réponse en fréquence comprise dans un intervalle englobant très largement la bande audio, par exemple de 2Hz à 100kHz. L'information hors de la bande audio n'est pas perçue par l'auditeur, par contre la courbe de réponse en fréquence sera plus lisse entre 20Hz et 20kHz car elle atteint le sommet du plateau bien avant 20Hz et ne redescend que bien après 20kHz, et les irrégularités sont principalement concentrées aux extrémités du spectre.
 |
La dynamique : Correspond au rapport entre l'intensité maximale et minimale des sons que l'on peut reproduire. Avec 90dB, soit un rapport de 109, le disque compact atteint la dynamique d'un orchestre symphonique dans une salle de bonne acoustique.
Le rapport signal sur bruit : Correspond au rapport entre l'intensité maximale que peut prendre le signal utile et le niveau du bruit de fond (c'est le souffle que l'on entend parfois). Encore une fois avec 90dB on atteint largement les conditions d'un concert classique.
Remarques : Le rapport signal sur bruit réel est malheureusement très souvent bien en deçà de la capacité théorique du disque compact. En effet, les ingénieurs du son effectuent souvent un mixage2 trop travaillé, ne règlent pas correctement le niveau des micros, ou tout simplement enregistrent dans un environnement bruyant.
En fait la qualité moyenne des prises de son est exécrable. Il est à noter à ce sujet que l'on peut obtenir d'aussi bons résultats avec un enregistrement analogique qu'avec un enregistrement numérique. Les trois lettres (AAD, ADD ou DDD) qui indiquent de quelle manière ont été réalisés respectivement, l'enregistrement, le mixage et la gravure (la troisième est superflue, la gravure est toujours numérique!) n'ont aucun rapport avec la qualité de l'enregistrement. On citera en référence de qualité, l'enregistrement analogique de Dark Side Of The Moon des Pink Floyd chez EMI enregistré en 1972(!) et numérique de La Symphonie Fantastique de Berlioz par Charles Dutoit chez DECCA en 1983.
 |
 |
|||||||||||||||||||
La séparation des canaux : C'est un paramètre très important pour la qualité de ``l'image'' stéréophonique. La diaphonie, c'est-&-grave; dire l'interférence entre les deux canaux gauche et droit, est inférieure à 90dB pour le disque compact, ce qui signifie que la proportion de signal gauche ``débordant'' sur le signal droit (ou réciproquement) est de 10-9.
La distorsion harmonique : Cette mesure, exprimée en pourcentage, indique l'altération des courbes harmoniques composant le signal. Cela peut se produire entre autres, en cas de saturation pendant une prise de son, les sinusoïdes se transforment alors en signal carré. La distorsion harmonique est inférieure à 0.004% pour le disque compact.
La linéarité de phase : Se mesure en degré et caractérise le déphasage entre le signal théorique et réel. Notre oreille est quasiment insensible au déphasage d'un signal monophonique, par contre la stabilité de l'image stéréo, donc la sensation de profondeur, dépend très largement de ce paramètre. C'est un paramètre extrêmement difficile à contrôler sur du matériel analogique, il est quasiment parfait sur le disque compact (+/- 0.5o).
Le pleurage et le scintillement : Caractérisent en pourcentage d'erreur, respectivement, la déformation du son due à une vitesse de lecture trop lente ou trop rapide du signal. Ces défauts sont inexistants sur le disque compact.
Il existe d'autres paramètres (temps de montée, distorsion d'intermodulation, etc...) mais ils sont moins significatifs. Pour certains d'entre eux on précise parfois si le calcul a été pondéré ou non. L'information la plus caractéristique dans un signal sonore est située en dessous de 3000Hz pour l'homme, ainsi toutes les fréquences n'ont pas la même importance, on introduit donc une pondération dans les calculs.
Remarque : La durée de vie d'un disque compact n'est pas illimitée comme on pourrait le croire. Des essais de vieillissement montrent qu'elle peut varier considérablement selon les conditions de stockage du disque. Une firme française à conçu un support beaucoup plus résistant et de bien meilleure qualité que le polycarbonate actuellement utilisé pour le pressage des C.D., et dont la durée de vie est de l'ordre de 1000 ans, malheureusement son prix le réserve aux sociétés qui ont besoin d'un support d'archivage très stable.
Les avantages du disque compact sont nombreux par rapport aux supports traditionnels, on a donc regroupé dans le tableau de la figure 5, à titre comparatif, les valeurs moyennes de quelques paramètres des trois supports les plus courants, à savoir le disque analogique, la cassette audio et le disque compact.
| Paramètres | Disque 33 tours | Cassette | C.D. |
|---|---|---|---|
| Taille (ou diamètre) | 30cm | 10 × 6 × 1 cm | 12cm |
| Durée de lecture | 40mn | 90mn | 75mn |
| Dynamique | 70dB | 70dB | >90dB |
| Rapport Signal/Bruit | 45dB | 65dB n.p. | >90dB n.p. |
| Séparation des canaux | 30dB | 50dB | >90dB |
| Réponse en fréquence | 30Hz-20kHz | 20Hz-20kHz | 20Hz-20kHz |
| Distorsion harmonique | 1-2% | <0.5% | 0.004% |
| Pleurage et scintillement | 0.03% | 0.03% | n.m. |
| Durée de vie | 500 H | Variable | 10-100 ans |
| Effet des altérations | parasites | parasites | corrigibles |
Aucune amélioration flagrante de qualité n'est à attendre au niveau de la source sonore avec la conception stéréophonique actuelle. Il est donc nécessaire pour la prochaine ``révolution'' de repenser au principe même de la transcription, soit en abandonnant la stéréophonie, soit, ce qui est plus vraisemblable, en développant les recherches sur les processeurs d'ambiance.
La légende veut que la durée de lecture du disque compact ait été déterminée après avoir consulté le chef d'orchestre H.V. Karajan. Il jugea qu'il fallait pouvoir enregistrer la neuvième symphonie de Beethoven d'un seul tenant. On arrive ainsi à 75mn, bien que ses propres interprétations de cette symphonie n'aient jamais excédé 69mn. La version moins poétique est que le disque compact devait pouvoir tenir dans un autoradio, sa taille limitait donc la durée d'exécution.
Nous allons maintenant décrire les grandes lignes de la conversion Analogique/Numérique utilisée pour le disque compact.
La conversion analogique-numérique
L'échantillonnage d'un signal sonore consiste à ne retenir que certains points de la courbe amplitude/temps, pour minimiser la quantité d'information à stocker. Ces points peuvent être choisis de façon périodique, l'échantillonnage est alors uniforme, ou de toute autre manière. C'est le type de signal que l'on veut échantillonner qui va déterminer la manière de choisir ces échantillons. Le seul objectif est de pouvoir reconstituer le signal à partir des échantillons prélevés.
Pour l'échantillonnage qui nous intéresse, on considère en fait toutes les fréquences comprises entre 0 et 20000Hz.
Vocabulaire : Le filtrage d'un signal consiste à éliminer certaines de ses composantes spectrales, par exemple les fréquences supérieures à une fréquence fmax. Dans ce cas précis on dira qu'on utilise un filtre passe-bas, et fmax sera appelée la fréquence de coupure du filtre. On définit similairement un filtre passe haut. Les fréquences supérieures (ou inférieures selon le filtre) à la fréquence fmax (fmin) ne sont pas éliminées brutalement, mais progressivement, à mesure qu'elles s'éloignent de la fréquence de coupure. On peut alors préciser la pente de la coupure, et on dira par exemple qu'un filtre passe-bas de fréquence de coupure 20kHz a une pente de 12dB par octave.
Le théorème de Shannon affirme qu'un signal peut être complètement défini à partir de ses échantillons. Dans le cas d'un signal dont le spectre est de type passe-bas, c'est-à-dire dont la bande de fréquence est comprise entre 0Hz et une fréquence maximale fmax, le critère de Nyquist indique comment réaliser l'échantillonnage : les échantillons doivent être prélevés à intervalles réguliers Te tel que Te <= 1/(2fmax). Autrement dit, on peut recomposer le signal si la fréquence d'échantillonnage fe = 1/Te est supérieure à deux fois la fréquence la plus haute contenue dans le signal.
Si la fréquence d'échantillonnage est inférieure à deux fois fmax alors on ne peut récupérer le signal sans distorsion à cause du phénomène de repliement des spectres (voir [17]) lors de la transformation de Fourier inverse. On retrouve évidemment cette situation si l'on échantillonne un signal à une fréquence fe = 2fmax et si son spectre s'étend au-delà de la fréquence maximale fmax supposée. Il est donc essentiel de filtrer le message avec un filtre passe-bas de fréquence de coupure fmax. La fréquence d'échantillonnage du disque compact est de 44.1kHz.
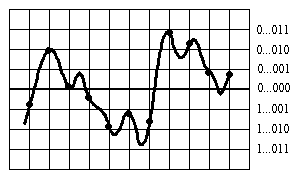
La numérisation du signal n'en est pas pour autant achevée, en effet, ces échantillons sont à valeur dans un intervalle réel, il y a donc une infinité de représentations. Pour remédier à cela, on pourrait arrondir les réels sur un certain nombre de décimales, mais on ne procède pas de cette manière. C'est à ce moment qu'intervient la Pulse Code Modulation de Reeves : on discrétise l'intervalle réel en 2n points équidistribués (on verra comment déterminer n), et on associe à chaque échantillon l'index du point le plus proche (figure 6). On quantifie donc chaque échantillon réel en un mot binaire de longueur n, la numérisation est alors achevée.
 |
Il faut bien mesurer la portée du théorème de Shannon3 : le signal est entièrement défini par les échantillons, il n'y a donc aucune perte d'information. Ce n'est pas le cas avec la quantification. L'erreur que l'on commet est appelée bruit de quantification. Ici la quantification est linéaire, on a donc à faire à un bruit blanc.4 On peut à partir de là calculer le rapport Signal/Bruit à l'aide de la formule
S/B = 6.02n + 1.76 dB
où n est la longueur d'un symbole (voir [3]). On obtient 98dB sur 16 bits et 86dB sur 14 bits. La quantification a été fixée à 16 bits pour le disque compact, de manière à ce que le rapport Signal/Bruit atteigne celui d'une salle de concert avec une bonne acoustique. En fait ce rapport est un peu plus faible car on ajoute au signal un léger bruit blanc analogique, de manière à éliminer la distorsion harmonique (due au bruit de quantification) sur les signaux de faible amplitude. En effet si un signal oscille dans la même bande de quantification, selon le moment ou l'on échantillonne, on obtiendra un signal continu ou carré (figure 7). C'est ce signal carré qui génère des harmoniques très aigüs, sources de distorsion. L'addition d'un bruit blanc analogique de faible amplitude élimine ce signal carré au prix d'une légère augmentation du bruit de fond.
 |
Remarque : La fréquence d'échantillonnage du disque compact provient du standard PAL de la télévision : une image est constituée de 625 lignes dont 37 sont inutilisables, et chaque ligne peut porter trois échantillons audio sur 16 bits, on a donc (625 - 37) x 3=1764 mots transmissibles par image. Il y a 25 images par seconde, on obtient alors 1764 × 25 = 44100 échantillons par seconde.
La conversion numérique-analogique
Pour la reconstitution du signal on dispose donc d'une séquence de mots binaires sur 16 bits qui représentent la courbe amplitude/temps du signal.
Un convertisseur N/A classique crée un courant électrique proportionnel à la valeur entière d'un mot et garde ce courant constant jusqu'à ce que le mot suivant apparaisse. Le signal ainsi reconstitué est en escalier.
Les variations abruptes du courant sur les ``marches'' engendrent des hautes fréquences nettement supérieures à 20kHz, inaudibles mais très destructrices pour l'amplificateur et surtout les enceintes. Il faut donc filtrer ces fréquences. On place alors un filtre passe-bas analogique à la sortie du convertisseur.
Remarques : Si on observe le spectre du signal en escalier, il apparait clairement que le filtrage est très délicat à réaliser. C'est pourquoi certains constructeurs comme Philips ont préféré réaliser un filtrage numérique avant la conversion. On procède alors à un suréchantillonnage du signal numérique qui convertit les mots de 16 bits à une fréquence de 44100Hz en mots de n bits à une fréquence m × 44100Hz. Pour Philips il s'agit d'un quadruple (m = 4) suréchantillonnage qui génère des mots de longueur 28. Certains constructeurs vont jusqu'à suréchantillonner 256 fois.
Le signal numérique étant beaucoup moins sensible aux perturbations que le signal analogique, on a tout intérêt à faire la conversion le plus tard possible, c'est-à-dire immédiatement avant l'amplification. C'est ce que font les amplificateurs ``numériques''. Le signal numérisé provenant d'un lecteur C.D. ou de tout autre appareil audio-numérique (D.A.T., Tuner, etc...) est reçu via un cable coaxial ou une fibre optique dans l'amplificateur. Ce signal est ensuite préamplifié numériquement, et c'est juste avant l'étage d'amplification que l'on procède à la conversion N/A. Cette technique tend à se généraliser car elle permet de réduire les coûts de fabrication des appareils, en effet, on élimine le (ou les) convertisseur(s) des sources audio-numériques au profit de celui (ceux) de l'amplificateur.