Algorithmique iii - Le problème des 8 reines

Problème et modélisation

Le problème initialement posé par K.F. Gauss en 1842 est le suivant : est-il possible de placer 8 reines sur un échiquier sans qu'aucune reine n'en menace une autre ? Gauss trouva lui-même 72 solutions à ce problème, mais nous verrons qu'il en existe 92, si l'on ne tient pas compte des symétries naturelles de l'échiquier. Pour ceux qui ne connaissent pas les règles du jeu d'échec, du moins la partie des règles qui concernent la reine, une reine menace toutes les pièces de l'échiquier qui sont situées sur la même :

  1. ligne ;
  2. colonne ;
  3. diagonale.
Cette contrainte est représentée dans l'échiquier de la figure 1. Nous utilisons l'indexation usuelle des tableaux, autrement dit la case de coordonnées \(\color{#FF0}(i,j)\) est située sur la \(i\)-ème ligne et la \(j\)-ème colonne dans le sens de lecture, contrairement au jeu d'échec où les lignes sont numérotées du bas vers le haut et les colonnes sont indexées par les 8 premières lettres de l'alphabet de A à H. Les cases menacées par la reine placée dans la case (4,5) contiennent deux épées croisées ⚔.
\(i\) \(\quad\quad j\)
La reine dans la case (i, j) menace les cases marquées de deux épées croisées ⚔ sur l'échiquier.

Ce problème se généralise à un échiquier fictif de taille \(n\times n\) où la question devient : quel est le nom­bre maximal de reines que l'on peut placer sur cet échiquier ? On note \(R(n)\) ce maximum.

Pour un échiquier de taille \(n\geq 1\), on a \begin{equation} R(n)\leq n. \end{equation}
En effet, d'après la première contrainte, il est impossible de placer plus d'une reine par ligne, le nombre total de reines ne peut donc excéder le nombre de lignes \(n\).
Les cas \(n=0,1,2,3\) sont simples à étudier à la main. On trouve \(R(0)=0\), \(R(1)=1\), \(R(2)=1\) et \(R_3=2\) (cf. oeis pour les valeurs \(n>14\), les autres étant calculées ici même). D'après le lemme, si ce maximum est atteint, il y a nécessairement une seule reine sur chaque ligne et une seule reine sur chaque colonne. Ce dernier résultat suggère une stratégie pour trouver une solution. Elle consiste à placer la première reine sur la première case libre de la première ligne, éliminer les cases désormais interdites sur l'échiquier et recommencer la même opération pour les lignes suivantes. S'il n'est impossible de placer la \((k+1)\)-ème reine parce que toutes les cases de la \((k+1)\)-ème ligne sont interdites, il faut revenir en arrière et déplacer la \(k\)-èeme reine sur la prochaine case libre, si elle existe, et si la situation ne se débloque pas, on remonte à la ligne précédente et ainsi de suite. C'est probablement la stratégie que le lecteur a appliquée pour vérifier les \(4\) premiers cas.

Observons cette stratégie en détail pour calculer \(R(4)\). Puisqu'il ne peut y avoir plus d'une reine par ligne, nous décrivons une solution par un simple quaduplet \(S\) où \(S[i]\) est la colonne où se trouve la reine placée sur la ligne \(i\). Notons qu'une solution \(S\) est donc une permutation du groupe symétrique \({\mathfrak S}_n\). Les échiquiers ci-dessous décrivent le processus dans l'ordre de lecture. Les reines sont placées/déplacées au fur et à mesure pour aboutir à la première solution \(\color{yellow}S=(2,4,1,3)\) :

\(1.\ \ S=(1, ?, ?, ?)\) \(2.\ \ S=(1, 3, ⚔, ?)\) \(3.\ \ S=(1, 4, ?, ?)\) \(4.\ \ S=(1, 4, 2, ⚔)\)
\(5.\ \ S=(2, ?, ?, ?)\) \(6.\ \ S=(2, 4, ?, ?)\) \(7.\ \ S=(2, 4, 1, ?)\) \(8.\ \ S=(2, 4, 1, 3)\)
Résolution du problème des 4 reines avec la méthode du backtracking. Les épées ⚔ marquent un échec et le futur backtracking.

Cette technique classique est appelée backtracking en informatique. Le backtracking (ou recherche en arrière en français) est un procédé de résolution qui est particulièrement adapté pour ce type de problèmes. On peut décrire le déroulement d'un jeu par un graphe dont les sommets sont les différents états du jeu et les arcs représentent les transitions d'un état à un autre. Dans le cas particulier où il est impossible de revenir à un état passé dans la chronologie du jeu, le graphe n'a pas de cycles et il s'agit donc d'un arbre. Le nombre maximal d'alternatives q pour passer d'un état à un autre du jeu fixe l'arité de l'arbre et le début du jeu est logiquement la racine de l'arbre. Un tel arbre est appelé arbre de décision. Le backtracking désigne une manière de parcourir un tel arbre et ce parcours est souvent implicite.

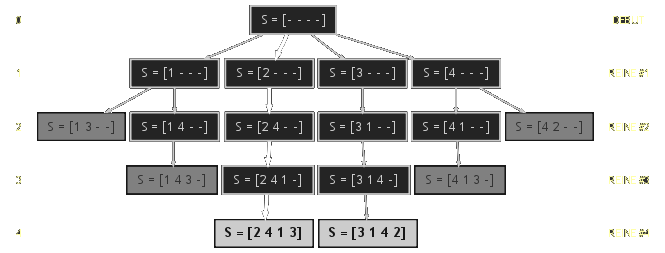
Dans la résolution du problème des 4 reines ci-dessus, le jeu commence avec un échiquier vide et on change d'état à chaque fois qu'une nouvelle reine est placée. L'arbre de décision du problème des 4 reines est un arbre quaternaire puisqu'il y a 4 façons possibles de placer la première reine sur la première ligne. L'arbre de décision de ce problème est donné dans la figure 3. Trouver une solution au problème revient à déterminer dans quelle colonne de la \(i\)-ème ligne il faut placer la \(i\)-ème reine, \(i\in[1,n]\). La solution \(S\) est donc représentée par un \(n\)-uplet. Chaque nœud de l'arbre contient l'état du quadruplet solution. Les feuilles de l'arbre en gris correspondent à des impasses, et les feuilles les plus claires correspondent à une solution. Le chemin fléché en blanc correspond à la solution trouvée précédemment. Comme on peut le constater, il y deux solutions dans cet arbre, ce qui n'a rien d'étonnant puisque le groupe de symétrie du jeu comprend les symétries horizontale, verticale et diagonales sur le centre de l'échiquier.

Le backtracking consiste donc à visiter l'ensemble des nœuds de l'arbre en partant de la racine et en choisissant de prendre systématiquement le chemin le plus à gauche qui n'a pas encore été suivi.

Arbre de décision du backtracking pour \(n\) = 4.
Il est souvent possible de représenter un jeu à l'aide d'un arbre quand bien même aucune règle n'empêche de revenir à un état précédent. C'est le cas du jeu d'échec par exemple, et il est clair que le retour à un état précédent de l'échiquier est artificiel et n'a aucun intérêt, il est donc possible d'éliminer ces cycles artificiels et de modéliser ce jeu à l'aide d'un arbre.

Description de l'algorithme

La solution du problème est codée sous la forme d'un tableau \(S\) de taille \(n\) qui représente le \(n\)-uplet solution, c'est-à-dire que \(S[i]\) est la colonne où il faut placer la \(i\)-ème reine.

L'algorithme EstLibre teste si la case à la ligne ligne et à la colonne colonne n'est pas menacée par les reines précédemment placées. Il n'est pas nécessaire de disposer d'une matrice booléenne pour savoir quelles sont les cases menacées ou non au fur et mesure de l'évolution de l'algorithme, les positions des reines sur les lignes qui précèdent suffisent et cette information est dans la table S. La vérification se fait en observant qu'aucune reine précédente n'est placée sur la même ligne, sur la même colonne ou les mêmes diagonales, comme le montre l'échiquier ci-dessous pour la case (4,4) distinguée par un point d'interrogation.

?
Les cases testées par l'algorithme EstLibre pour vérifier si l'on peut placer la reine dans la case ? sont marquées d'un drapeau ⚑.

Comme le montre la figure 4, La case de coordonnées (4,4) n'est pas libre, elle est menacée par la reine qui a été placée en position (1,1) au premier appel de l'algorithme. 

EstLibre(S,ligne,colonne):booléen
données
   ligne,colonne: entiers
   S[1,n]: tableau d'entiers
variables
   l,c: entiers
   ok: booléen
DEBUT
   ok ← VRAI
   l ← 1
   TQ (l ≤ ligne) FAIRE
      c ← S[l]
      ok ← ok ET (|ligne - l| ≠ |colonne - c|) ET (colonne ≠ c)
      l ← l + 1            
   FTQ
   RETOURNER ok
FIN

L'algorithme PlacerReine est chargé de placer les reines les unes après les autres en parcourant implicitement l'arbre de décision. Contrairement à la résolution du problème des 4 reines présenté précédemment, l'algorithme ne s'arrête pas dès que les \(n\) reines sont placées mais poursuit son investigation dans l'arbre jusqu'au bout. Les \(n\) alternatives de placement d'une reine sur une ligne se concrétisent dans l'algorithme par une boucle suivie d'un test pour vérifier que la case candidate n'est pas menacée. Le premier appel de l'algorithme se fait avec la valeur 1.

L'algorithme Traiter n'est pas défini, il peut s'agir de l'affichage de la solution \(S\), ou du rangement de \(S\) dans une liste des solutions, ou tout autre traitement. 

PlacerReine(ligne)
données
   ligne: entier
variables globales
   n: entier
   S: tableau de taille n
variables
   colonne: entier
DEBUT
   SI (ligne > n) ALORS
      Traiter(S)
   SINON
      colonne ← 1      
      TQ (colonne ≤ n) FAIRE
         SI EstLibre(S,ligne,colonne) ALORS
	    S[ligne] ← colonne
	    PlacerReine(ligne + 1)
	    S[ligne] ← 0
         FSI
         colonne ← colonne + 1
      FTQ					 
   FSI
FIN

Montrez que la complexité de l'algorithme EstLibre est linéaire en la taille \(n\) de l'échiquier. On code à présent les contraintes sur une ligne de l'échiquier avec une structure de vecteur caractéristique. Le \(j\)-ème bit du vecteur caractéristique indique si la case à la colonne \(j-1\) est en échec (1) ou non (0). Supposons que \(k\) reines ont déjà été placées sur les \(k\) premières lignes et que l'on veuille placer la \((k+1)\)-ème reine. On se donne quatre vecteurs caractéristiques \(R_k\), \(V_k\), \(G_k\) et \(D_k\) pour coder les contraintes sur la \(k\)-ème ligne : Initialement pour placer la première reine, il n'y a aucune contrainte, donc \(R_1=V_1=G_1=D_1=0\). Si la pre­mière reine est placée sur la deuxième case, les contraintes pour la deuxième reine, pour un échiquier de taille \(n=8\), sont : \begin{equation*} \begin{matrix} & 0 & 1 & 2 & 3& 4 & 5 & 6 & 7\\ R_2=2:& 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ V_2=2:& 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ G_2=1:& 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ D_2=4:& 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{matrix} \end{equation*} On note \(S\) la permutation solution. Une fois que la \(k\)-ème reine a été placée, on connaît donc les \(k\) premières va­leurs de \(S\). Montrez que pour tout \(k>0\) : \begin{align} R_{k} &= 1 \ll (S[k] - 1)\\ V_{k+1} &= V_k \vee R_k\\ G_{k+1} &= (G_k \vee R_k) \ll 1\\ D_{k+1} &= (D_k \vee R_k) \gg 1\\ \end{align} En déduire que les positions où peut être placée la \(k\)-ème reine sont données par le vecteur caractéristique \begin{equation} \neg (G_k\vee D_k\vee V_k). \end{equation} En déduire un nouvel algorithme récursif PlacerReine qui exploite ce résultat pour se passer de l'algorithme EstLibre. Quel est le gain en terme de complexité ?
Vous pouvez voir l'intégralité des solutions trouvées par l'algorithme PlacerReine pour n'importe quel entier \(n\) tel que \(0\leq n \leq 14\) (L'algorithme a été implanté en javascript en tenant compte de l'amélioration suggérée dans l'exercice ci-dessus. Noter qu'il faut quelques secondes de calcul pour \(n=14\)). Saisissez la taille de l'échiquier \(n:=\)

Solution au problème des reines.

Donnez une condition nécessaire pour qu'une solution du problème des \(n+1\) reines fournisse une solution au problème des \(n\)-reines en supprimant la dernière ligne et la dernière colonne. Donnez une condition nécessaire pour qu'une solution du problème des \(n\) reines fournisse une solution au problème des \(n+1\) reines en étendant l'échiquier dans l'une des 4 directions no, ne, so ou se et en plaçant une reine dans l'angle correspondant.

Validité de l'algorithme

Nous laissons la preuve de l'algorithme EstLibre au lecteur. L'algorithme PlacerReine se termine puis­qu'à chaque appel récursif la variable ligne est incrémentée, elle atteindra donc la valeur \(n\) + 1 qui est traitée dans la base récurrente de l'algorithme. La justesse de l'algorithme se prouve à l'aide d'une récurrence sur le prédicat \(P(k)\) suivant :

“après le \(k\)-ème appel, la reine placée ne menace aucune des \(k - 1\) reines précédemment placées sur l'échiquier.”

Les travaux pratiques permettront de vérifier expérimentalement qu'il n'est pas envisageable de chercher l'ensemble des solutions au problème des \(n\) reines avec cette méthode pour \(n\geq 20\), si l'on veut le faire en temps raisonnable (il faut environ 45 minutes de calcul sur un processeur pentium core i5 pour calculer \(R(18)=666.090.624\)).

Complexité de l'algorithme

La complexité telle qu'elle a été définie dans le chapitre concernant les fonctions de complexité n'est pas précisément adaptée à ce que l'on souhaite mettre en évidence ici, nous dérogerons donc à la règle qui veut que l'on exprime la complexité en fonction de la taille de l'entier \(n\) plutôt que \(n\) lui-même.

Ainsi, nous ne tenons pas compte du traitement de la solution et nous supposerons que le coût de la base récurrente est constant \(\Theta(1)\) (cf. remarque plus loin). Dans la partie sinon de l'algorithme, le coût des instructions hors de la boucle est constant soit \(\Theta(1)\). À chaque appel, on passe \(n\) fois dans la boucle. Le nombre de cases libres sur une ligne diminue au moins d'une unité quand on passe à la ligne suivante, le test EstLibre est donc satisfait au plus \(n-k+1\) fois à la ligne \(k\), donc \begin{equation*} T(n)\leq\begin{cases} \Theta(1),&\text{si}\ n=1,\\ \Theta(1)+n\big(\Theta(1)+T(n-1)\big),&\text{sinon}. \end{cases} \end{equation*} Que l'on peut réécrire \begin{equation}\label{eq:complex} T(n)\leq\begin{cases} \Theta(1),&\text{si}\ n=1,\\ \Theta(n)+nT(n-1),&\text{sinon}. \end{cases} \end{equation} En substituant \(T(k)\) successivement \(n\) fois dans (\ref{eq:complex}), on aboutit à \begin{align*} T(n)&\leq n!T(1)+\sum_{k=0}^{n-1}\frac{n!}{(n-k)!}\Theta(n-k)\\ &\leq \Theta(n!) \end{align*} ce qui nous mène à la conclusion : \begin{equation} \hat T(n)=O(n!) \end{equation} Le premier exercice ci-dessous propose une minoration de la fonction de complexité.

l'hypothèse qui consiste à négliger le traitement de la solution dans la base récurrente de l'algorithme peut sembler arbitraire mais se justifie par le fait que le nombre de feuilles/solutions de l'arbre de récursion est négligeable comparé au nombre de feuilles/impasses qui activent le backtracking. Ainsi intégrer le coût du traitement de la solution, que l'on peut légitimement supposer en Ω(\(n\)), dans l'expression récurrente de la fonction de complexité ci-dessus fausserait le calcul à coup sûr vu notre méthode d'estimation basée sur l'arité de l'arbre de récursion.
Montrez qu'à chaque fois qu'une reine est placée à une ligne \(k\), il y a au plus trois cases supplémentaires de la ligne \(k\) + 1 qui sont menacées. En déduire qu'une impasse ne peut être découverte avant la profondeur \(n\)/3 dans l'arbre de récursion et minorez la fonction de complexité de l'algorithme.
Modifiez l'algorithme pour qu'il s'arrête dès qu'il a trouvé une solution. La complexité de l'algorithme est-elle changée ?

Travaux pratiques

Écrivez l'algorithme en langage \(C\) et vérifiez qu'il y a bien 92 solutions au problème des huit reines. Déterminez le groupe de symétrie du jeu et calculer le nombre de solutions distinctes modulo ce groupe.

Tracer la courbe de temps en fonction de \(n\) avec l'utilitaire Gnuplot pour les premières valeurs de \(n\). à partir de quelle valeur de \(n\) le programme ne répond-il plus instantanément ? Quelle est la valeur maximale approximative de \(n\) qui vous paraît raisonnable de traiter ?