Plus Longues Sous-séquences Communes

Quelques définitions

On rappelle (voir ordre lexicographique) que si \(A\) est un alphabet fini, \(A^*\) désigne la fermeture de Kleene de \(A\), c'est-à-dire l'ensemble des séquences (suites finies) de symboles de \(A\) que l'on appelle mots. Cet ensemble est muni d'une loi de composition interne \(\cdot\) appelée concaténation, on inclut dans \(A^*\) le mot vide \(\varepsilon\) qui est l'élément neutre pour cette loi. Par exemple avec l'alphabet \(A:=\{0, 1\}\), on a \(A^*=\{\varepsilon,0,1,00,01,\ldots\}.\) Le nombre de symboles d'un mot \(u\) est appelé longueur du mot que l'on note indif­fé­rem­ment \(|u|\) ou \(\#u\). On appelle langage sur l'alphabet \(A\) tout sous-ensemble \(L\) de \(A^*\). On étend la loi de con­ca­té­na­tion entre mots de \(A^*\) aux mots de deux langages \(L,M\subseteq A^*\) par \begin{equation} L.M:=\{u.v\ |\ u\in L\ \text{et}\ v\in M\}. \end{equation} Par abus de langage, si \(s\in A^*\) et \(L\subseteq A^*\), on note \(s.L\) l'ensemble \(\{s\}.L\) et \(L.s\) l'ensemble \(L.\!\{s\}\).

Soit \(A\) un alphabet fini et \(u\) et \(v\) deux mots de \(A^*\). On dit que \(u\) est une sous-séquence de \(v\), ce que l'on note \(u\preceq v\), si \(n\leq m\) et s'il existe \(j:[1,n]\rightarrow[1,m]\) croissante qui satisfait \(u_i=v_{j(i)}\) pour tout \(i\in[1,n]\) où \(n:=|u|\) et \(m:=|v|\).

En mathématique, une sous-séquence \(u\) d'un mot \(v\) est aussi appelée suite extraite de \(v\). Con­crè­te­ment \(u\preceq v\) signifie que l'on peut retrouver chaque symbole de \(u\) dans le mot \(v\) et dans le sens de lecture.

Montrez que la relation binaire \(\preceq\) est une relation d'ordre total sur \(A^*\). Soient \(n\) et \(k\) deux entiers positifs tels que \(0\leq k\leq n\). Combien existe-t-il de sous-séquences de longueur \(k\) d'une séquence de longueur \(n\) ? En déduire qu'il existe exactement \(2^n\) sous-séquences d'une séquence de longueur \(n\).
(1) Sur l'alphabet \(A:=\{a,b,c\}\), le mot \(v=\color{yellow}baabc\) est une sous-séquence du mot \(u=a{\color{yellow}b}c{\color{yellow}aab}a{\color{yellow}c}\). Il faut noter qu'il peut y avoir plusieurs applications crois­santes \(j\) qui déterminent une même sous-séquence.
(2) Sur l'alphabet latin \(A:=\{a,b,\ldots,z\}\), les mots \(u={\color{yellow}a}{\color{red}l}go{\color{yellow}r}ith{\color{yellow}me}\) et \(v=larme\) ont les mots \(\color{yellow}arme\) et \({\color{red}l}\color{yellow}rme\) comme plus longues sous-séquences communes.
Soient \(u,v,w\in A^*\) telles que \(w\preceq u\) et \(w\preceq v\). On dit que \(w\) est une plus longue sous-séquence commune (plsc en abrégé) de \(u\) et \(v\) si \begin{equation}\label{def:plsc} \forall x\in A^*,\quad \ (x\preceq u\ \text{et}\ x\preceq v)\Rightarrow |x|\leq |w| \end{equation} On note \(\Pi(u,v)\) le langage des plsc de \(u\) et \(v\) et \(\Lambda(u,v)\) la longueur d'une plsc de \(u\) et \(v\).

Les deux lemmes suivants sont faciles à établir et seront utiles pour démontrer le résultat principal sur lequel s'appuie l'algorithme.

Soient \(u,v\in A^*\) et \(\alpha\in A\). Alors \begin{equation} u\preceq v\ \Leftrightarrow u.\alpha\preceq v.\alpha \end{equation}
Soient \(u,v\in A^*\) avec \(u=u_1u_2\ldots u_n\) et \(v=v_1v_2\ldots v_m\). Alors \begin{equation} (u\preceq v\ \text{et}\ u_n\not=v_m)\Rightarrow u\preceq v_1v_2\ldots v_{m-1}. \end{equation}
Démontrez les deux lemmes précédents.

Présentation du problème et première partie de l'algorithme

En bio-informatique l'étude du génome amène les chercheurs à comparer des brins d'adn. Un brin d'adn est constitué exclusivement de 4 nucléotides dont l'assemblage moléculaire est caractéristique du brin. On le modélise très facilement comme un mot sur l'alphabet \(\{A, C, G, T\}\) dont les sym­bo­les désignent respectivement les nucléotides Adénine, Thymine, Cytosine et Guanine. Il faut trouver un outil adéquat pour comparer les brins ou en trouver les points communs. Dans un autre registre, comment mesurer la similitude entre deux fichiers informatiques (commande diff du système unix), ou encore quel est le mot le plus proche d'un mot donné ? Toutes ces interrogations trouvent une réponse possible avec la recherche des plus longues sous-séquences communes.

Écrivez un algorithme EstSS(u,v) qui décide (i.e. qui renvoie vrai ou faux) si \(u\) est une sous-séquence de \(v\). Indication : une simple boucle suffit, comparez les symboles \(u[i]\) et \(v[j]\) en incrémentant judicieusement les indices \(i\) et \(j\) initialisés à 1. Calculez la complexité de votre algorithme.

L'objectif est d'écrire un algorithme efficace pour chercher les plus longues sous-séquences communes de deux séquences données \(u\) et \(v\). Une approche naïve est possible, on peut par exemple construire toutes les sous-séquences de \(u\) et toutes les sous-séquences de \(v\) puis rechercher parmi les sous-séquences communes quelle est/sont la/les plus longue(s). Le résultat de l'exercice 1 nous incite à fuir cette approche. En effet, si on note \(U\) et \(V\) l'ensemble des sous-séquences de \(u\) et \(v\) respectivement, on sait que \(\#U=2^{|u|}\) et \(\#V=2^{|v|}\) et il faudrait donc \(2^{|u|}+2^{|v|}\) opérations pour calculer \(U\) et \(V\) dans un premier temps. Il resterait encore à calculer l'intersection \(U\cap V\) de ces deux ensembles soit \(2^{|u|}\times 2^{|v|}\) opérations supplémentaires si on comparait un-à-un les éléments de \(u\) avec ceux de \(v\), et pour finir \(\#U\cap V\) opérations pour en extraire le(s) mot(s) le(s) plus long(s). Soit au final une complexité de l'ordre de \(\Theta(2^{|u|+|v|})\) ce qui est considérable.

En supposant que ce que nous avons qualifié d'opération dans le paragraphe précédent coûte un cycle d'une machine cadencée à 2,3Ghz, quelles sont les longueurs maximales de deux brins d'adn si l'on veut en déterminer les plus longues sous-séquences communes en moins d'une heure ?

On peut faire mieux et nous allons opérer en deux phases. La première consiste à calculer \(\Lambda(u,v)\) et la seconde à déterminer une plsc ou toutes les plsc. Nous verrons que selon que l'on veut calculer une ou l'ensemble des plsc, la complexité de l'algorithme est très différente.

Soit \(u=u_1u_2\ldots u_n\in A^*\). On appelle équeuté de \(u\) le préfixe \(u':=u_1u_2\ldots u_{n-1}\) si \(n>1\) et \(u':=\varepsilon\) sinon. Le résultat suivant permettra de justifier l'algorithme :

Soient \(u,v,w\in A^*\) de longueurs respectives \(n,m\) et \(k\). Si \(w\in\Pi(u,v)\), alors
  1. \(u_n=v_m\Rightarrow w_k=u_n\ \text{et}\ w'\in\Pi(u',v')\)
  2. \(u_n\not= v_m\Rightarrow w\in\Pi(u,v')\ \text{ou}\ w\in\Pi(u',v)\)
1. Dans un premier temps, montrons par l'absurde que \(u_n=v_m\Rightarrow w_k=u_n\). Notons \(\alpha\) le symbole de \(A\) tel que \(u_n=v_m=\alpha\) et supposons que \(w_k\not=\alpha\). On sait que \(w\in\Pi(u,v)\) donc \(w\preceq u'.u_n\) et \(w\preceq v'.v_m\) soit \(w\preceq u'\) et \(w\preceq v'\) d'après le lemme 3. Le lemme 4 nous permet d'en déduire que \(w.\alpha\preceq u\) et \(w.\alpha\preceq v\) soit \(w.\alpha\in\Pi(u,v)\). Mais d'après (\ref{def:plsc}) on a \(|w.\alpha| \leq |w|\) soit \(|w|+1\leq |w|\) ce qui est contradictoire.

On a donc \(w_k=u_n=w_m=\alpha\), montrons que \(w'\in\Pi(u',v')\). On a \(w\in\Pi(u,v)\) donc \(w\preceq u'.\alpha\) et \(w\preceq v'.\alpha\) soit \(w'.\alpha\preceq u'.\alpha\) et \(w'.\alpha\preceq v'.\alpha\) soit \(w'\preceq u'\) et \(w'\preceq v'\) d'après le lemme 3 et finalement \(w'\in\Pi(u',v')\).

2. On a \(w\in\Pi(u,v)\) donc \(w\preceq u'.u_n\) et \(w\preceq v'.v_m\). Comme \(u_n\not=v_m\), on a nécessairement \(w_k\not=u_n\) ou \(w_k\not= v_m\). Supposons que \(w_k\not=u_n\). D'après le lemme 4, on déduit que \(w\preceq u'\) et ainsi que \(w\in\Pi(u',v)\). Dans l'autre cas, le raisonnement est symétrique ce qui achève la dé­mons­tra­tion.

Le théorème fournit immédiatement une définition récurrente de l'ensemble \(\Pi(u,v)\) et l'algorithme récursif n'est que la traduction de cette définition : \begin{equation}\label{defrec:Pi} \Pi(u,v):= \begin{cases} \varepsilon&\text{si}\ u=\varepsilon\ \text{ou}\ v=\varepsilon,\\ \Pi(u',v').u_n&\text{si}\ u_n=v_m,\\ \Pi(u',v)\cup\Pi(u,v')&\text{si}\ u_n\not=v_m. \end{cases} \end{equation}

Et il ne reste plus qu'à le traduire en algorithme : 
PLSCRec(u,v):liste de mots
données
   u,v: mots
variables
debut
   SI (u = ε OU v = ε):
      retourner []
   SINON SI u[#u] = v[#v]:
      retourner PLSCRec(u',v').u[#u]
   SINON: 
      retourner PLSCRec(u',v) + PLSCRec(u,v')
FIN.

Dans cet algorithme, les opérateurs \(\color{yellow}.\) et \(\color{yellow}+\) désignent respectivement la concaténation des mots et la concaténation des listes. Malheureusement sa complexité (que nous étudierons dans la section suivante) est en \(\Theta(2^{\min\{|u|,|v|\}})\) à cause des deux appels récursifs. Nous allons procéder différemment en éliminant la récursivité. On déduit immédiatement de (\ref{defrec:Pi}) un corollaire sur \(\Lambda(u,v)\) :

\begin{equation}\label{defrec:Lambda} \Lambda(u,v):= \begin{cases} 0&\text{si}\ u=\varepsilon\ \text{ou}\ v=\varepsilon,\\ \Lambda(u',v') + 1&\text{sinon et si}\ u_n=v_m,\\ \max\{\Lambda(u',v),\Lambda(u,v')\}&\text{sinon et si}\ u_n\not=v_m. \end{cases} \end{equation}

L'expression (\ref{defrec:Lambda}) montre que pour calculer \(\Lambda(u,v)\) il suffit de connaître les trois quantités \(\Lambda(u',v)\), \(\Lambda(u,v')\) et \(\Lambda(u',v')\). Notons \(n:=|u|\) et \(m:=|v|\). On définit la matrice entière \(L\) de dimension \((n+1)\times (m+1)\) par \begin{equation}\label{eq:matrice} L_{i,j}:=\begin{cases} \Lambda(u_1u_2\ldots u_i, v_1v_2\ldots v_j)&\text{si}\ i>0\ \text{et}\ j>0,\\ 0&\text{sinon}. \end{cases} \end{equation}

Ainsi, si l'on calcule les termes de la matrice dans l'ordre de lecture, de gauche à droite puis de haut en bas, on dispose toujours des 3 quantités \(\color{#6464FF}\Lambda(u',v)\), \(\color{yellow}\Lambda(u,v')\) et \(\color{orange}\Lambda(u',v')\) qui sont disposées géographiquement à l'ouest, au nord et au nord-ouest et servent à calculer \(\color{red}\Lambda(u,v)\).

Exemple : On considère les mots \(u={\color{white}algorithme}\) et \(v={\color{white}larme}\) : \begin{equation} \begin{matrix} L & j & 0 & 1 & 2 &\color{red}\bf 3 & 4 & 5\\ i & & \varepsilon &\color{red} l &\color{red} a &\color{red} r &\color{white} m &\color{white} e\\ 0 & \varepsilon & 0 & 0 & 0 & 0 & 0 & 0\\ 1 &\color{red} a & 0 & 0 & 1 & 1 & 1 & 1\\ 2 &\color{red} l & 0 & 1 & 1 & 1 & 1 & 1\\ 3 &\color{red} g & 0 & 1 & 1 & 1 & 1 & 1\\ 4 &\color{red} o & 0 & 1 & 1 & 1 & 1 & 1\\ 5 &\color{red} r & 0 & 1 & \color{orange}1 & \color{#6464FF}2 & 2 & 2\\ \color{red}\bf 6 &\color{red} i & 0 & 1 & \color{yellow}1 & \color{red}\bf 2 & 2 & 2\\ 7 &\color{white} t & 0 & 1 & 1 & 2 & 2 & 2\\ 8 &\color{white} h & 0 & 1 & 1 & 2 & 2 & 2\\ 9 &\color{white} m & 0 & 1 & 1 & 2 & 3 & 3\\ 10 &\color{white} e & 0 & 1 & 1 & 2 & 3 & 4 \end{matrix} \end{equation}

La valeur \(\color{red}L_{6,3}=2\) correspondant à la longueur \(\Lambda({\color{red}algori},{\color{red}lar})\) ne dépend que des valeurs \(\color{yellow}L_{6,2}=1\), \(\color{#6464FF}L_{5,3}=2\) et \(\color{orange}L_{5,2}=1\).

Soient \(u,v\in A^*\) deux séquences définies sur un alphabet \(A\). Alors \begin{equation} \Lambda(u,v)=L_{|u|,|v|} \end{equation}
Par construction de la matrice \(L\), cf. (\ref{eq:matrice}).
Écrivez l'algorithme récursif LplscRec qui renvoie la longueur d'une plus longue sous-séquence commune des mots \(u\) et \(v\) en entrée et qui s'appuie sur la récurrence (\ref{defrec:Lambda}).
L'algorithme itératif pour calculer \(\Lambda(u,v)\) s'en déduit mais renvoie la matrice \(L\) qui servira dans la suite plutôt que la seule valeur \(L_{|u|,|v|}=\Lambda(u,v)\) : 
LPLSC(u,v):matrice entière
données
   u,v: mots
variables
   L: matrice d'entiers 
   i,j: entiers
debut
   Allouer(L,(|u|+1)*(|v|+1),0)
   i ← 1   
   TQ i ≤ #u:
      j ← 1
      TQ j ≤ #v:
         SI u[i] = v[j]:
            L[i,j] = L[i-1,j-1] + 1
         SINON:
            L[i,j] = max(L[i-1,j],L[i,j-1])
         j ← j + 1
      i ← i + 1
   renvoyer L
FIN

Deuxième partie de l'algorithme

Maintenant que nous disposons des longueurs des plus grandes sous-séquences communes, nous pouvons facilement trouver une plsc. La définition récurrente de \(\Lambda\) en (\ref{defrec:Lambda}) précise quelle règle a été appliquée pour la construction de la matrice. Réciproquement, on va construire un chemin dans la matrice \(L\) qui part de l'angle sud-est de coordonnées \(i\leftarrow|u|\) et \(j\leftarrow|v|\) pour rejoindre la ligne 0 ou la colonne 0 et reconstituer une plsc \(w\) initialisée au mot vide \(\varepsilon\) :

  1. Si \(u_i = v_j\) on concatène cette valeur à gauche de \(w\), i.e. \(w\leftarrow u_i.w\) et on se déplace en \((i - 1, j - 1)\).
  2. Sinon on compare les valeurs au nord et à l'ouest de \((i,j)\) :
    1. Si \(L_{i - 1, j} > L_{i, j - 1}\) on se déplace au nord en \((i - 1, j)\);
    2. Si \(L_{i - 1, j} < L_{i, j - 1}\) on se déplace à l'ouest en \((i, j - 1)\);
    3. Si \(L_{i - 1, j} = L_{i, j - 1}\) on se déplace soit
      1. en \((i-1, j)\) et en \((i, j - 1)\) (algorithme récursif déterministe).
      2. en \((i-1, j)\) ou en \((i, j - 1)\) (algorithme itératif potentiellement non-déterministe).

Deux possibilités s'offrent au point B.3  selon que l'on cherche à déterminer l'ensemble \(\Pi(u,v)\) dans son intégralité ou une plsc arbitraire. La définition (\ref{defrec:Lambda}) montre que dans ce cas elle a été obtenue in­dif­fé­rem­ment à partir de l'un des deux maximums, on peut donc continuer la construction d'une plsc par le nord ou par l'ouest. On a donc implicitement un arbre de décision.

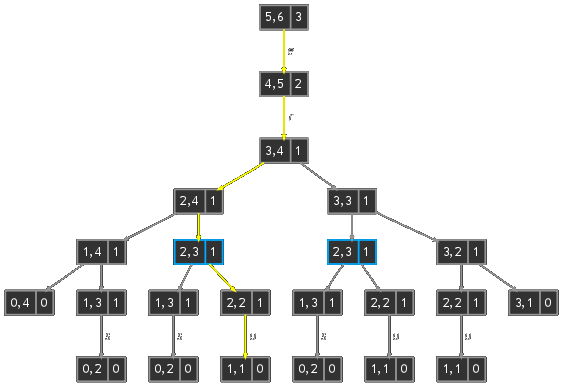
Pour comprendre cette construction, étudions le cas des séquences \(u=sucre\) et \(v=lustre\). On calcule tout d'abord la matrice \(L\) : \begin{equation} \begin{matrix} L & j & 0 & 1 & 2 &\color{red}\bf 3 & 4 & 5 & 6\\ i & & \varepsilon &\color{red} l &\color{red} u &\color{red} s &\color{red} t &\color{white} r &\color{white} e\\ 0 & \varepsilon & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 &\color{red} s & 0 & \color{yellow}\bf0 & 0 & 1 & 1 & 1 & 1\\ 2 &\color{red} u & 0 & 0 & \color{yellow}\bf1 & \color{yellow}\bf1 & \color{yellow}\bf1 & 1 & 1\\ 3 &\color{red} c & 0 & 0 & 1 & \color{#6464FF}\bf1 &\color{yellow}\bf1 & 1 & 1\\ 4 &\color{white} r & 0 & 0 & 1 & 1 & 1 &\color{yellow}\bf 2 & 2\\ 5 &\color{white} e & 0 & 0 & 1 & 1 & 1 & 2 & \color{yellow}\bf3\\ \end{matrix} \end{equation} Le chemin commence en \(\color{yellow}(5,6)\) avec \(w=\varepsilon\) et se poursuit en \(\color{yellow}(4,5)\) avec \(w=e\) puisque \(u_5=v_6=e\), continue en \(\color{yellow}(3,4)\) avec \(w=re\) puisque \(u_4=v_5=r\). À ce stade le chemin peut bifurquer au nord en \(\color{yellow}(2,4)\) ou à l'ouest en \(\color{#6464FF}(3,3)\) puisque \(u_3=c\not=t=v_4\) et que \({\color{yellow}L(2,4)}={\color{#6464FF}L(3,3)}=1\). L'arbre de décision est représenté ci-dessous, un nœud contient les indices \(i\) et \(j\) à gauche et \(L_{i,j}\) à droite et quand \(u_i=v_j\) la branche est étiquettée par le symbole correspondant. Le chemin choisi est en jaune dans la matrice et dans l'arbre de décision et fournit la plsc \(w=ure\). L'arbre montre qu'il en existe une deuxième \(sre\) et que chacune des deux peut être obtenue par trois chemins distincts.

Arbre de décision de l'algorithme des plsc pour \(u=sucre\) et \(v=lustre\). Les deux nœuds en couleurs forment des sous-arbres identiques.
Le chemin choisi correspond à l'utilisation de la règle B.3.ii. dans l'écriture de l'algorithme. Si on prend certaines décisions au hasard, l'algorithme sera non-déterministe mais on peut évidemment le déterminiser en choisissant systématiquement le nord par exemple. La construction de l'ensemble \(\Pi(u,v)\) est obtenue avec le choix B.3.i qui consiste à appeler récursivement l'algorithme pour parcourir les deux branches à chaque décision.

Écrivez un algorithme itératif PlscIt(u,v) qui renvoie une plsc et un algorithme récursif PlscRec(u,v) qui renvoie la liste constituée par tous les mots de \(\Pi(u,v)\). Vous utiliserez dans les deux cas l'algorithme Lplsc(u,v) qui renvoie la matrice \(L\).

Complexité

Dans la suite nous notons \(n:=|u|\) et \(m:=|v|\). Commençons par l'analyse de l'algorithme Lplsc. L'algorithme construit la matrice \(L\), on peut donc se contenter de compter le nombre d'éléments qui détermine son coût global, il n'y a pas de cas favorable ou défavorable, on a donc une complexité en \(\Theta(nm)\).

Pour rechercher une seule plsc, il faut trouver le chemin le plus court qui part de l'angle sud-est de la matrice \(L\) et qui aboutit à la ligne ou à la colonne \(\varepsilon\), autrement dit le minimum de \(n\) et \(m\) auquel il faut rajouter le coût de la construction de la matrice \(L\) soit

\begin{equation}\label{eq:compit} \Theta(nm) + \Theta(\min\{n,m\}) = \Theta(nm). \end{equation}

Si l'on veut calculer \(\Pi(u,v)\) avec l'algorithme récursif il faut remarquer qu'il y a deux appels ré­cur­sifs à chaque fois que les symboles sont différents et que les deux valeurs au nord et à l'ouest sont égales. On définit alors implicitement un arbre binaire dont la profondeur est majorée par un chemin de longueur maximale entre les angles Sud-Est et Nord-Ouest, soit \(n+m\) ce qui nous donne une complexité exponentielle de \(O(2^{n+m})\) dans le pire des cas.

En reprenant les hypothèses de l'exercice 2, quelles sont les longueurs maximales de deux brins d'adn si l'on veut en déterminer les plus longues sous-séquences communes en moins d'une heure  avec la complexité de l'algorithme itératif de complexité (\ref{eq:compit}) ?
Les deux nœuds étiquetés \(2,3\;{\color{#079ADA}|}\;1\) montrent dans l'arbre de décision de la figure 1 que des chemins peuvent se rejoindre et que leurs sous-arbres sont identiques. La conséquence est que les appels récursifs évaluent plusieurs fois des branches inutilement. À l'aide d'un tableau de booléens, modifiez l'algorithme récursif pour qu'une branche qui a déjà été évaluée lors d'un appel ne le soit plus dans les suivants (procédé dit de mé­moï­sa­tion).

Travaux pratiques

Vous pouvez vérifier que vos programmes renvoient des résultats corrects en saisissant les deux chaînes de caractères \(u\) et \(v\), puis en validant :

\(\phantom{v}u=\)
\(\phantom{u}v=\)

On obtient la matrice \(L\) suivante :

On en déduit que \(\Lambda(u,v)\) =  et que .

Écrivez une première fonction Python LPLSC-REC(u,v) qui renvoie la longueur des plus longues sous-séquences communes entre les chaînes de caractères \(u\) et \(v\) de manière récursive. Déclarez un compteur en variable globale et comptez le nombre d'appels à votre fonction pour des mots \(u\) et \(v\) de longueurs croissantes et sans lettres communes. Tracez la courbe du nombre d'appels en fonction de \(|u|+|v|.\) Écrivez la version itérative LPLSC(u,v) à partir de l'algorithme Lplsc et tracez à nouveau la courbe du nombre d'appels. Comparez les deux courbes.
Écrivez une fonction Python PLSC-IT(u,v) qui renvoie une plus longue sous-séquence commune entre les chaînes de caractères \(u\) et \(v\). Écrivez une fonction Python PLSC-REC(u,v) qui renvoie toutes les plus longues sous-séquences communes entre les chaînes de caractères \(u\) et \(v\).
[Solution en C]
[Solution en Python]