Le barème est donné à titre indicatif et est sus­cep­tible d'être adapté. Lisez at­ten­ti­ve­ment les explications. Commentez vos fonctions.

L'objectif est d'écrire un programme en langage C  qui calcule les codes de Huffman des symboles d'un alphabet 𝒜 pour la compression de texte. L'alphabet 𝒜 est volontairement limité ici aux 26 lettres majuscules.

Présentation du problème

Chaque lettre x_i d'un mot x construit sur l'alphabet 𝒜 est encodé par une séquence binaire h(x_i) où la fonction h: 𝒜 → {0,1}* est déterminée à partir des fréquences des symboles du texte, de manière à ce que h(a) soit d’autant plus court que a y est fréquent.

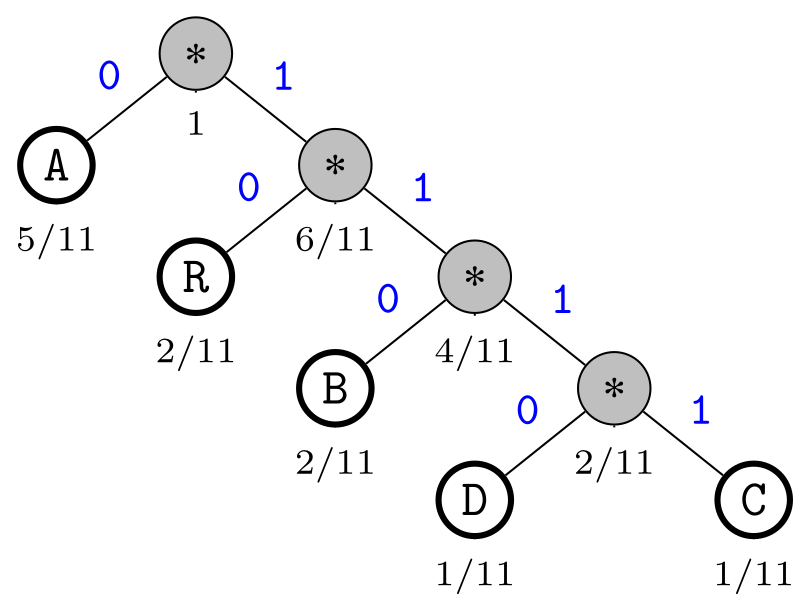
Le code de Huffman h(a) du symbole a est défini comme la concaténation des étiquettes binaires rencontrées sur le chemin qui relie la racine d'un arbre binaire valué à la feuille a : 0 pour les branches gauches, 1 pour les branches droites.

a	pa ≈	h(a)
A	5/11	0
B	2/11	110
C	1/11	1111
D	1/11	1110
R	2/11	10

Le principe de construction de l'arbre de Huffman est très simple :

1. On calcule la fréquence de chaque symbole de 𝒜 présent dans le texte à compresser. Par exemple A, B, C, D et R dans x = ABRACADABRA (cf. table ci-dessus).
2. On part d'une forêt contenant autant d'arbres réduits à un unique nœud constitué par chaque symbole de 𝒜 présent dans le texte et valué par sa fréquence (ce sont les 5 feuilles cerclées de gras dans la figure).
3. Tant qu'il reste au moins 2 nœuds :
   1. chercher les deux noeuds avec la plus petite valuation (D et C dans notre exemple initialement).
   2. créer un nœud père dont ce sont les fils (celui de plus petite fréquence à gauche), valué par la somme de leurs fréquences (2/11 = 1/11 + 1/11). Ces nœuds internes (sur fond gris) sont marqués par le symbole *.

Le mot CAR serait donc compressé en 1111010 := 1111·0·10.

Un tas minimal est un tas pour la relation d'ordre inverse, autrement dit la valuation de chaque nœud est inférieure à celle de ses fils s'ils existent, donc T[1] contient l'élément de plus petite valuation. Si ses éléments sont les symboles de 𝒜 et la valuation leur fréquence, ce tas permet de trouver le symbole de fréquence minimale en Θ(1) pour construire l'arbre de Huffman.

Les éléments du tas seront des pointeurs vers des quadruplets

typedef struct tquad {
    uchar symb;              // Un symbole de A ou '*'
    float freq;              // Sa fréquence d'apparition
    struct tquad *fg, *fd;  // Fils gauche et droit
} tnoeud;

typedef tquad *tnoeud;  

On aura donc deux structures d'arbre :

1. la première est implicite, c'est l'APO associé au tas.
2. la seconde est explicite, c'est l'arbre de Huffman qui sera le fruit des liens que l'algorithme va tisser entre les quadruplets contenus dans le tas.

Construction de l'arbre avec un tas minimal

Votre travail se limitera à compléter certaines fonctions de base du programme huffman.c à télécharger (les plus difficiles sont fournies).

Une fois le fichier source compilé par la commande :

$ gcc -o huffman huffman.c -Wall

L'appel

$ ./huffman ABRACADABRA

A: 0
B: 110
C: 1111
D: 1110
R: 10

Pour éviter d'adapter les algorithmes du cours sur les tas dont l'indexation commence à 1, la structure de tas contient 1 élément supplémentaire (le terme T[0] reste donc inutilisé) et on intègre le nombre d'éléments qu'il contient dans la structure qui le code :

typedef struct {
    tarbre T[NBSYMB + 1]; // Tableau 1-indicé
    size_t taille;        // Nombre d'éléments dans le tas
} ttas;