Introduction

Algorithmes et algorithmique

Définition naïve

Nous utilisons des algorithmes en permanence, non seulement en mathématiques et en informatique ou plus généralement dans le domaine des sciences, mais tout simplement dans la vie quotidienne pour réaliser une quantité de tâches incroyablement variées. Nous nous servons d'algorithmes pour nous habiller, préparer un café, calculer le montant de nos impôts, vérifier l'état d'un véhicule, etc. La définition suivante est une synthèse des multiples définitions du mot algorithme gla­nées dans les dic­tion­nai­res.

On appelle algorithme tout procédé de résolution d'un problème en un nombre fini d'étapes par application d'une série de règles prédéfinies.

Notons immédiatement qu'il n'est nullement fait mention d'un ordinateur dans cette définition, à jus­te titre puisqu'on a pu retrouver des algorithmes datant de plusieurs milliers d'années. Les ba­by­lo­niens développaient déjà des algorithmes de factorisation ou d'extraction de racines carrées 1600 ans avant JC.

L'archétype de l'algorithme est la recette de la tarte aux pommes. Elle décrit les opérations élé­men­tai­res à réaliser pour l'obtention de la tarte (la sortie) à partir des ingrédients (l'entrée) :

Recette de la tarte aux pommes

Les 10 opérations successives de la préparation composent l'algorithme et décrivent comment pro­cé­der pour ré­sou­dre ce problème. Elles font apparaître trois struc­tu­res syntaxiques caractéristiques des algorithmes :

  1. La structure séquentielle : les opérations se font successivement, les unes après les autres, elles sont ici numérotées de \(1\) à \(10\).
  2. La structure répétitive : elle est implicite et inconditionnelle dans couper 4 pommes en morceaux et explicite et conditionnelle dans jusqu'à ce que le sucre soit roux.
  3. La structure conditionnelle : elle est explicite dans Si le bord de la pâte est trop large.

Le pâtissier professionnel s'intéressera sans aucun doute à la complexité des recettes, et préfèrera une recette qui de­man­de 20 minutes de préparation à une autre qui en demande 45 (pour un ré­sul­tat iden­ti­que s'en­tend).

La recette proposée ici est suffisamment détaillée pour un être humain, mais elle souffre de quelques li­mi­ta­tions. Elle ne précise pas comment préparer une compote de pommes (ce qui justifierait l'écri­tu­re d'un algorithme spécifique, tout comme la préparation de la pâte si elle n'était pas toute faite), ni comment allumer et régler le four selon sa nature (à bois, électrique, au gaz ?). Elle s'adresse ma­ni­fes­te­ment à une personne adulte qui a des connaissances préalables en cuisine. Si nous devions décrire tout ceci à un enfant, il faudrait sans doute décomposer ces opérations en tâches plus simples et certaines d'entres elles en d'autres plus simples encore.

Cette approche appelée analyse des­cen­dan­te définit implicitement un parcours ar­bo­res­cent et constitue une tech­ni­que fon­da­men­ta­le pour écrire des algorithmes. Comme nous l'avons fait remarquer, la finesse de la dé­com­po­si­tion de certaines tâches est dépendante du public auquel s'adresse la recette. Il en ira de même pour l'implantation d'un algorithme selon le modèle de calcul utilisé. L'effort à fournir pour écrire un pro­gram­me en langage Python n'est pas le même qu'avec un langage d'as­sem­bla­ge.

L'algorithmique est le domaine des sciences qui étudie les règles et les tech­ni­ques impliquées dans la conception et l'analyse des algorithmes et plus généralement la struc­tu­ra­tion des données et des opé­ra­tions.

L'objectif principal de l'algorithmique est de concevoir des méthodes efficaces pour automatiser la résolution d'un problème. La conception d'un algorithme n'est donc qu'une partie de cet objectif, il faut également s'assurer qu'il est efficace, ce qui se traduit dans ce contexte par une économie des ressources en temps et en espace. Les deux aspects sont abordés à la fois dans la phase de conception et la phase d'analyse qui ne sont pas indépendantes, elles constituent le fil rouge de ce cours.

Définition formelle

Même si notre première définition résume de manière tout à fait sa­tis­fai­san­te le concept, elle est inu­ti­li­sa­ble en l'état pour en faire le socle d'une théorie. Le problème est similaire à celui qu'a rencontré le mathématicien G. Cantor quand il a voulu définir for­mel­lement le concept d'ensemble et édicter des règles pour les construire. Sa définition et le principe d'abstraction (tout prédicat engendre un ensemble constitué des éléments qui le satisfont) abou­tis­saient im­man­qua­ble­ment à des paradoxes, et il a fallu attendre les travaux de Zemelo et Fraenkel sur la théorie des ensembles (souvent résumée en théorie zf) pour comprendre qu'il était nécessaire d'établir des règles strictes pour construire de nouveaux ensembles à partir du germe que constitue l'ensemble vide \(\varnothing\). Les travaux ultérieurs du mathématicien K. Gödel ont alors permis de cerner les limites de toute théorie ma­thé­ma­tique.

Les recherches effectuées par les mathématiciens pour formaliser la notion de calcul ou d'algorithme, et ceci avant même que le simple mot ordinateur n'existe, ont été aussi prolifiques et précieuses que celles qui ont abouti à la théorie zf utilisée de nos jours. Il existe d'ailleurs de multiples intersections entre ces deux théories. De nombreux modèles mathématiques ont été pro­po­sés pour cadrer au plus juste ce concept et on sait aujourd'hui que tous sont équivalents. Au­tre­ment dit, ce que l'on est ca­pa­ble de résoudre comme problèmes, ou ce que l'on est en mesure de calculer, ne dépend pas du modèle algorithmique choisi — du moment que ce modèle respecte les propriétés universellement reconnues comme caractéristiques d'un algorithme — en particulier celles que nous avons mises en évidence dans l'ex­emp­le de la recette de la tarte aux pommes. C'est ce que con­jec­tu­rait le logicien américain Alonzo Church, inventeur du \(\lambda\)-calcul, avant même que l'on ne prouve formellement l'équi­va­len­ce des mo­dè­les abstraits en lice. Le chapitre suivant est consacré à l'étude d'un modèle formel proche des or­di­na­teurs, La machine ram. La définition formelle d'un algorithme est donc liée à un modèle abstrait et sera présentée dans le chapitre consacré au modèle ram.

La structuration et l'expression d'un calcul est intimement liée au modèle considéré, elle est souvent qualifiée de programme. Dans ce contexte formel, algorithme et programme sont donc sy­no­ny­mes. Si la façon d'exprimer un algorithme est très variable, son mode opératoire reste largement indépendant du modèle mathématique considéré. Un algorithme traite des données initiales constituant son entrée en construisant de nouvelles quantités dont certaines, une fois le calcul achevé, sont interprétées comme un résultat, sa sortie.

Si programme et algorithme sont synonymes dans un contexte formel, c'est-à-dire dans un modèle de calcul abstrait, il en va autrement en pratique. Pour faire une mé­ta­phore, en in­for­ma­ti­que l'algorithme est au pro­gram­me ce qu'un plan d'architecte est au plan d'exécution dans la cons­truc­tion. Le premier est un schéma qui décrit les grandes lignes de l'ouvrage, le second spécifie les moin­dres détails (réseaux, cotes, coupes, to­po­gra­phie, matériaux, engins et outils disponibles pour la cons­truc­tion, etc.) En pratique, un programme est une description effective sur machine d'un algorithme. Il comporte des pro­blé­ma­ti­ques pro­pres et spécifiques au langage employé.

Une deuxième approche imagée est de considérer un algorithme comme une machine physique qui traite une matière première (les ingrédients de la tarte aux pommes) pour la trans­for­mer en produit fini (la tarte aux pommes). La description du fonctionnement rudimentaire d'un hachoir à viande devrait suffir à comprendre l'hypotypose.

   matière \(\Downarrow\) première
\(\Rightarrow\) produit fini
Ceci n'est pas un hachoir à viande

La viande en morceaux est fournie en entrée dans l'entonnoir et la rotation de la manivelle l'entraîne vers le couteau à l'aide d'une vis sans fin. La machine renvoie en sortie la viande hachée.

L'articulation entre un algorithme et ses entrées/sorties est parfaitement modélisée par une fonction mathématique. En effet, l'écriture schématique \[x\stackrel{f}{\longmapsto}y\] d'une fonction mathématique \(f\) résume parfaitement la dynamique d'un algorithme. L'idée suggérée par cette écriture en la lisant de gauche à droite est qu'un objet \(x\) est transformé en un objet \(y\) par l'entremise de la fonction \(f\). Dans certains cas, cette tran­sfor­ma­tion peut être décrite à l'aide d'une expression algébrique, com­me par exemple \(x\mapsto x^2 -3x + 1\), ce qui cadre bien avec l'idée naïve que l'on se fait d'un calcul. Une autre écriture classique d'une fonction précise la nature des objets \(x\) et \(y\) en spécifiant l'ensemble de départ et l'ensemble d'arrivée : \begin{equation} %\bbox[border:1px solid white; padding:12px]{ f:\begin{matrix} E\rightarrow F\\ {\color{yellow}x}\mapsto \color{#BBF}y \end{matrix}%} \end{equation} On peut résumer cette articulation par un schéma qui s'en inspire fortement : \(\color{yellow}x\) est assimilé à l'entrée de l'algorithme, \(\color{#BBF}y\) à la sortie, les ensembles de départ et d'arrivée précisent le type des données, et la fonction \(f\) joue le rôle de l'algorithme  :

entrée
\(x:=\,\)		 \(\xrightarrow[]{\phantom{\text{entrée}}}\) algorithme
\(f\) 		\(\xrightarrow[]{\phantom{\text{sortie}}}\) sortie
\(y=\,\)

Algorithme : premier schéma fonctionnel. Saisissez une valeur de \(x\) pour calculer \(x^2-3x+1\).

Il ne faut pas déduire de cette analogie que toute fonction ma­thé­ma­ti­que est un algo­ri­th­me. Si tout algorithme définit implicitement une fonction, la réciproque est fausse de manière gé­né­ra­le. L'objet de la théorie de la calculabilité abordée dans le cadre du cours de complexité al­go­ri­thmi­que du master est pré­ci­sé­ment l'étude de cette réciproque.

Nous allons affiner ce premier schéma. L'entrée comme la sortie sont modélisées respectivement par deux mots définis sur un alphabet d'entrée \(\Sigma\) et un alphabet de sortie \(\Gamma\)L'ensemble des mots sur un alphabet \(A\) est noté \(A^*\). L'entrée du programme est obtenue via un schéma d'encodage qui désigne de manière un peu pompeuse une façon de traduire les données réelles et bien concrètes de notre monde en objets abstraits qui pourront être manipulés par des outils d'une théorie mathé­mati­que. Par exemple un triplet \(({\color{#F00}R},{\color{#0F0}V},{\color{#00F}B})\in[0,255]^3\) de trois octets peut représenter la couleur d'un pixel sur un écran. C'est ce que j'ai fait ici même avec les codes hexadécimaux \(\color{#F00}\verb+F00+\), \(\color{#0F0}\verb+0F0+\) et \(\color{#00F}\verb+00F+\) pour distinguer ces trois couleurs res­pec­ti­ve­ment dans le texte. Symétriquement, la sortie du programme est elle même interprétée à l'aide d'un schéma de décodage. Notons pour finir qu'un jeu de paramètres particuliers d'un problème est qualifié d'instance du problème et que l'entrée \(x\) d'un algorithme est le mot de \(\Sigma^*\) qui en résulte via le schéma d'encodage. La taille d'une instance est la longueur du mot \(x\in\Sigma^*\), c'est-à-dire le nombre de ses symboles. La figure ci-dessous résume tout ceci :

Langage naturel Langage abstrait Modèle de calcul abstrait Langage abstrait Langage naturel
instance \(\xrightarrow[]{\text{encodage}}\) \(x\in\Sigma^*\) \(\xrightarrow[]{\phantom{\text{entrée}}}\) algorithme programme \(\xrightarrow[]{\phantom{\text{sortie}}}\) \(y\in\Gamma^*\) \(\xrightarrow[]{\text{décodage}}\) résultat
Question entrée calcul sortie Réponse
Algorithme : encodage, calcul puis décodage.

Nous n'avons par encore spécifié la manière dont les informations doivent être manipulées par un algorithme. Tous les modèles abstraits intègrent l'aspect séquentiel des étapes à franchir pour ré­sou­dre le problème ainsi que la définition d'un ensemble fini de règles strictes pour assurer cette pro­gres­sion. Le déterminisme de l'algorithme est également fondamental, son comportement doit être par­fai­te­ment défini en toute circonstance et reproductible. En ce sens, le pa­ra­di­gme de pro­gram­ma­tion qui est suggéré par cette approche est la pro­gram­ma­tion impérative qui décrit comment ré­sou­dre un problème. La pro­gram­ma­tion déclarative est un autre pa­ra­di­gme de pro­gram­ma­tion dans lequel on fournit une description du problème à travers des structures, fonctions, relations, ou des con­train­tes.

Calculer la somme des valeurs obtenues en jetant \(10\) fois de suite un dé à \(6\) faces constitue-t-il un algorithme ? Justifiez votre réponse.

Un premier problème

À titre d'illustration, étudions un premier problème. On veut déterminer si un mot est un pa­lin­dro­me, c'est-à-dire si ce mot s'écrit exactement de la même façon à l'endroit et à l'envers comme le mot radar par exemple. Le problème se généralise souvent à des phrases entières en ne tenant compte que des lettres et en omettant les espaces et autres symboles. Par exemple la phrase suivante*

(*) Saisissez vos propres mots ou phra­ses dans la zone de saisie ci-contre.

un palindrome. Le mot sévir qui s'écrit rivés à l'envers n'est pas un palindrome mais un ana­cyc­li­que car dans les deux sens le mot a un sens…

Ce problème est extrêmement simple à résoudre, il suffit de comparer les lettres du mot avec celles de ce même mot écrit à l'envers. Mais si la procédure décrite par la phrase comparer les lettres du mot avec celles de ce même mot mais écrit à l'envers est limpide pour un être humain, il est vrai­sem­bla­ble qu'il faudra encore de sérieuses avancées en informatique avant qu'une machine ne soit en mesure de l'interpréter pour élaborer l'outil qui décide si un mot est un palindrome ou non.

Trouver une méthode générale pour résoudre un problème est une première victoire, mais il reste quelques étapes à franchir avant d'être en mesure d'en extraire un programme informatique qui plus est efficace. En effet, la méthode décrite dans notre phrase est imprécise, incomplète et ambiguë. Elle est suffisante pour un être humain car il est cap­able de

Tout ce travail préparatoire, que nous faisons en partie inconsciemment, reste encore insurmontable pour une machine, il faut donc l'expliciter dans les moindres détails. C'est l'une des principales dif­fi­cul­tés de l'algorithmique et l'aptitude à décortiquer, analyser et abstraire nos idées est une qualité que partagent l'informaticien et le mathématicien. On peut considérer que l'on a réel­le­ment compris comment résoudre un problème si l'on est capable d'écrire un programme pour le faire.

L'analyse du problème permet de fixer un cadre théorique adéquat pour sa résolution et ainsi de choisir les modèles de données les mieux adaptés pour y parvenir. On parle parfois d'algèbre de conception. Ce sont les structures algébriques utilisées en mathématiques qui sont les outils pri­vi­lé­giés pour représenter les objets à manipuler. Nous verrons que les modèles de données informatiques sont majoritairement des structures algébriques bien connues ou des déclinaisons plus ou moins fi­dè­les de ces structures. Ces modèles de données sont à leur tour déclinés en structures de données dans les langages de programmation.

Dans le cadre de la résolution du problème du palindrome, la théorie des langages, tout au moins une part homéopathique, s'avère adaptée à sa description formelle. On se donne un ensemble fini \(A=\{a_0,a_1,\ldots,a_{q-1}\}\) appelé alphabet constitué des lettres ou symboles \(a_i\). Toute séquence \(u\) de \(n\) lettres de \(A\) est appelée mot de longueur \(n\), longueur que l'on désigne par \(|u|\) ou \(\#u\). On note \(A^n\) l'ensemble (fini) de tous les mots de longueur \(n\) et \(A^*\) l'ensemble (infini) de tous les mots possibles. Par analogie avec les langues na­tu­rel­les et par éco­no­mie, on écrit les termes d'une séquence sans les séparer par des virgules. Le miroir d'un mot \(u=u_1u_2\ldots u_n\) est le mot \(u_nu_{n-1}\ldots u_1\). Un langage est un sous-ensemble de \(A^*\). Par exemple, la langue française est un langage, c'est un sous-ensemble fini de tous les mots que l'on peut constituer avec les symboles de l'alphabet latin \(A=\{a,b,c,\ldots,z\}\). Le mot algorithme est un mot de la langue française contrairement au mot ahhhlborythme.

Un mot de \(n\) lettres de la langue française est donc modélisé par un mot (abstrait) \(u=u_1u_2\ldots u_n\) de longueur \(n\). Ce passage du réel au formel et le choix que nous avons fait pour représenter un mot de la langue française constitue précisément un schéma d'encodage. Dans ce cas précis, ce passage est simple et ne pose aucune difficulté. À présent, savoir si un mot \(u=u_1u_2\ldots u_n\) est ou non un pa­lind­rome se traduit mathématiquement par la valeur de vérité de la proposition \begin{equation}\label{eq:egseq} %\stackrel{?}{=} ou \overset{?}{=} u_1u_2\ldots u_n \stackrel{?}{=} u_nu_{n-1}\ldots u_1 \end{equation}

Soit \(A\) un alphabet fini. Deux mots \(u=u_1u_2\ldots u_n\) et \(v=v_1v_2\ldots v_m\) de \(A^*\) sont égaux si et seulement si \begin{equation}\label{eq:egseq2} n=m\quad \text{et}\quad \forall i\in [1,n]\ \ u_i=v_i. \end{equation}
Cela résulte de l'égalité des deux applications \(u:[1,n]\rightarrow A\) et \(v:[1,m]\rightarrow A\), soit l'égalité de leurs ensembles de départ, d'arrivée et de leurs graphes (axiome d'extension : deux ensembles \(X\) et \(Y\) sont égaux si et seulement si \(X\subseteq Y\) et \(Y\subseteq X\)).

Ce lemme permet de valider formellement cette approche et l'assertion (\ref{eq:egseq2}) suggère un procédé ité­ra­tif pour s'assurer que l'égalité (\ref{eq:egseq}) est satisfaite ou non : en notant \(v\) le miroir de \(u\), il suffit de vérifier que l'égalité \(u_i=v_i\) est satisfaite pour tous les indices \(i\) variant de \(1\) à \(n\). Si à une étape \(i\) donnée \(u_i\not=v_i\), on peut affirmer que \(u\) n'est pas un palindrome sans avoir à poursuivre les vérifications. En revanche si toutes ces égalités ont été vérifiées, on peut affirmer que \(u\) est un palindrome.

On peut résumer tout ceci par un algorithme qui procède en deux phases, la première construit le mot miroir \(v\) (lignes #1 à #2b), la seconde com­pa­re \(u\) et \(v\) terme à terme (lignes #3 à #5) :

algorithme palindrome 1
  1. On fixe une variable \(i\) à la valeur \(1\) 
  2. Tant que \(i\leq n\) :
    1. On construit le \(i\)-ème terme \(v_i:=u_{n-i+1}\) du mot miroir \(v\),
    2. On incrémente \(i\) (i.e. on rajoute 1 à \(i\)).
  3. On fixe \(i\) à la valeur \(1\) 
  4. Tant que \(i\leq n\) et \(u_i=v_i\) :
    1. On incrémente \(i\)
  5. Si \(i>n\) alors \(u\) est un palindrome, sinon \(u\) n'est pas un palindrome.

Il est manifeste que le nombre d'instructions exécutées pour décider si un mot \(u\) est un palindrome ou non, dépend de la longueur \(n\) du mot \(u\) sans même définir précisément ce que l'on entend par instruction. Mais ce nombre d'instructions dépend également de la nature du mot, en effet, comme nous l'avons déjà remarqué, il est inutile de continuer les comparaisons dès que l'on a trouvé deux symboles \(u_i\) et \(v_i\) distincts, ce qui peut survenir bien avant d'atteindre la fin du mot. Nous allons dans ce chapitre et en première approximation considérer que chaque ligne de cet algorithme définit une instruction, notion qui sera formalisée au chapitre suivant.

Les instructions #1, 3 et 5 ne sont exécutées qu'une seule fois. Les instructions #2a et 2b le sont \(n\) fois chacune. L'instruction #2 est exécutée \(n+1\) fois. Pour un mot \(u\) donné, notons \(p(u)\in[1,n+1]\) la plus petite valeur de \(i\) telle que la condition \(i\leq n\) et \(u_i=v_i\) n'est plus satisfaite, soit : \begin{equation*} p(u) := \min\{i\in[1,n+1]\ \ |\ \ i>n\ \text{ou}\ u_i\not=v_i\}. \end{equation*} Alors l'instruction #4 est exécutée \(p(u)\) fois et l'instruction #4a exactement \(p(u)-1\) fois. Fi­na­le­ment en sommant, on en dénombre \begin{equation} 3+2n+(n+1)+p(u)+(p(u)-1)=3n+2p(u)+3. \end{equation} Le nombre d'instructions exécutées est minimal quand les deux premiers symboles sont distincts, i.e. quand \(u_1\not=v_1\), soit \(3n+5\) instructions puisque \(p(u)=1\). Le maximum est atteint quand \(u=v\), soit \(5n+5\) instructions si \(p(u)=n+1\).

Soit \(A\) un alphabet fini et \(u\in A^*\). Démontrez que dans l'algorithme ci-dessus, on peut remplacer la condition \(i\leq n\) dans l'instruction #4 par \(i\leq\lfloor\frac{n}{2}\rfloor\) où \(\lfloor x\rfloor\) désigne la partie entière du nombre réel \(x\), i.e. le plus grand entier inférieur ou égal à \(x\). Indication : montrez que \(u\) est un palindrome si et seulement si \(\forall i\in[1,\lfloor\frac{n}{2}\rfloor],\ u_i=v_i\).

Le lecteur avisé aura deviné qu'il est possible d'être plus économe pour décider si un mot \(u\) est un palindrome ou non avant même que l'exercice précédent ne suggère de modifier la fin de la boucle. On peut faire encore mieux en évitant tout simplement de construire préalablement le mot \(v\)  et en comparant directement les symboles de \(u\) entre eux :

Algorithme palindrome 2
  1. On fixe un indice \(i\) à la valeur \(1\) 
  2. Tant que \(i\leq \lfloor\frac{n}{2}\rfloor\) et \(u_i=u_{n-i+1}\) :
    1. On incrémente \(i\)
  3. Si \(i>\lfloor\frac{n}{2}\rfloor\) alors \(u\) est un palindrome, sinon \(u\) n'est pas un palindrome.

Il y a cette fois \(2\lfloor\frac{n}{2}\rfloor +3\) instructions qui sont exécutées dans le pire des cas et \(3\) dans le meilleur des cas, ce qui est bien meilleur qu'avec notre premier algorithme.

Réécrivez l'algorithme ci-dessus en parcourant simultanément le mot \(u\) de la gauche vers la droite et de la droite vers la gauche à l'aide de deux indices \(i\) et \(j\) respectivement initialisés à \(1\) et \(|u|\). Quelle est la condition de la boucle Tant que  dans ce cas ? Combien d'instructions sont exécutées dans le meilleur des cas et dans le pire des cas ? Dans quelle mesure cet algorithme est-il plus satisfaisant que les deux autres indépendamment de leurs complexités ?
On se propose d'évaluer le nombre moyen de tests effectués par cet algorithme, c'est-à-dire le nombre de fois où l'algorithme va évaluer l'expression logique (on néglige le test final après la boucle qui permet de conclure) : \begin{equation} \label{eq:testpal} (i\leq \left\lfloor\frac{n}{2}\right\rfloor)\ \ \wedge\ \ (u_i=u_{n-i+1}). \end{equation} On veut calculer cette moyenne en fonction de la longueur \(n\) des mots. La motivation initiale pour cet algorithme était évidemment liée à la langue française, mais dans ce cas l'analyse en moyenne nécessiterait une étude exhaustive des mots de notre langue pour chaque longueur \(n\) possible.

Pour simplifier le problème et permettre une analyse plus générale, on suppose que l'on dispose d'un alphabet \(A\) de cardinal \(q\), que l'espace des instances de l'algorithme est le langage \(A^n\) et que toutes les instances sont équiprobables. Notons que cette hypothèse d'équiprobabilité est très éloignée de la réalité, un mot de longueur 3 de la langue française qui commence par \(qu\) est certainement suivi par l'une des voyelles \(e,i\) ou \(o\).

L'expérience aléatoire consiste donc à tirer un mot \(u\) de \(A^n\) au hasard, l'espace d'échantillonnage \(\Omega\) est alors le langage \(A^n\). On note \(p(u)\) le nombre de fois où l'expression \((\ref{eq:testpal})\) a été évaluée lors de l'exécution de l'algorithme pour l'instance \(u\). Pour \(k\in[1,\lfloor\frac{n}{2}\rfloor+1]\), on définit l'évènement \[\Omega_k:=\{u\in \Omega\ |\ p(u)=k\}.\]

(1) Justifiez que \begin{equation} \label{eq:probaprod} \text{Prob}\,[\Omega_k] = \begin{cases} \text{Prob}\,[u_{k}\not=v_{k}]\times\displaystyle\prod_{i=1}^{k-1} \text{Prob}\,[u_i=v_i]&\text{si}\ k\in[1,\lfloor\frac{n}{2}\rfloor],\\ \displaystyle\prod_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor} \text{Prob}\;[u_i=v_i]&\text{si}\ k=\lfloor\frac{n}{2}\rfloor+1. \end{cases} \tag{$\Pi$} \end{equation} (2) Montrez que \begin{equation*} \forall i\in[1,\lfloor\frac{n}{2}\rfloor],\quad \text{Prob}\;[u_i=v_i]=\frac{1}{q}\ \text{et}\ \text{Prob}\;[u_i\not=v_i]=1-\frac{1}{q} \end{equation*} (3) Montrez que les évènements \(\Omega_k\) sont incompatibles.

(4) Montrez qu'aucun des ensembles \(\Omega_k\) n'est vide.

(5) Montrez que la réunion des ensembles \(\Omega_k\) est l'ensemble \(\Omega:=A^n\).

(6) En déduire que le nombre moyen de tests pour traiter un mot de longueur \(n\) est égal à \begin{equation} \label{eq:sum} \left(\frac{1}{q}\right)^{\lfloor\frac{n}{2}\rfloor}+ (q-1){\color{orange}\underbrace{\sum_{k=1}^{\lfloor\frac{n}{2}\rfloor}k\left(\frac{1}{q}\right)^{k}}_{S}}. \end{equation}

(7) Calculez l'expression \((\ref{eq:sum})\). Indication : cf. chapitre de combinatoire pour calculer la somme \(\color{orange}S\).

(8) Quelle est le nombre moyen de tests effectués, asymptotiquement sur la longueur des mots ?

Cette étude nous a permis de mettre en évidence les 4 grandes étapes à franchir pour passer d'un problème à sa résolution à l'aide d'un algorithme :

  1. modélisation du problème ;
  2. conception de l'algorithme ;
  3. preuve d'arrêt et de validité de l'algorithme ;
  4. analyse de la complexité de l'algorithme (mesure des performances).
Nous n'avons pas réellement fourni une preuve de la validité de l'algorithme, mais simplement exhibé l'élément clef (cf. exercice 1). Une approche systématique des preuves des algorithmes sera introduite en troisième année, avec la logique de Hoare. L'analyse des performances des algorithmes de­vien­dra rapidement le point central de leur étude grâce à leurs fonctions de complexité.
Programmez l'algorithme #2 et adaptez-le pour vérifier qu'une phrase constitue un palindrome ou non en ne tenant compte que des lettres (sans faire la distinction entre majuscules et mi­nus­cu­les) et pas des autres symboles dans la phrase (espaces, ponctuations, etc.).

Programmation

L'écriture d'un programme informatique dans un langage particulier pour la résolution effective d'un problème constitue une 5ème étape qui recèle elle aussi des difficultés, de nature et de magnitude différentes selon le langage utilisé. Il faut en premier lieu trouver les structures correspondant aux modèles utilisés ou les construire quand elles n'existent pas. Par exemple la gestion des chaînes de caractères et des listes en Python est simple et agréable alors qu'elle est particulièrement délicate et fastidieuse en langage C (avec d'autres atouts en contrepartie).

Adaptons les deux algorithmes de décision sur le palindrome présentés à la section précédente en langage Python et observons à travers cet exemple quelques écueils inhérents à la programmation  : 

def Est-Palindrome1(u):
    n = len(u)
    v = ""
    i = 0
    while (i < n):
        v = u[i] + v
        i = i + 1
    i = 0
    while (i < n) and (u[i] == v[i]):
        i = i + 1
    return (i >= n)     

def Est-Palindrome2(u):
    n = len(u)
    i = 0
    while (i < n//2) and (u[i] == u[n - (i + 1)]):
        i = i + 1
    return (i >= n//2)
Mentionnons pour commencer l'extraordinaire maladresse (c'est un point de vue très personnel) com­mise lors de la conception du langage C, à savoir coder l'affectation à l'aide du symbole ma­thé­ma­ti­que \(=\) dont la signification universelle est l'égalité. Ce choix imposait un codage différent pour l'égalité logique, d'où le bégaiement \(==\). Le concepteur de Python, Guido van Rossum, a jugé bon de reproduire cet impair qui constitue pourtant une source inépuisable d'erreurs. Le langage Pascal (et quelques autres), plus inspiré sur ce point, code l'affectation avec les deux symboles \(:=\), ce qui a l'énorme avantage, en rendant l'écriture asymétrique, d'appuyer sur la dynamique temporelle lorsque nous lisons une opération d'affectation (de la gauche vers la droite). Cette notation a d'ailleurs été adoptée par les mathématiciens pour distinguer une assertion comme \[\forall (x,y)\in {\mathbf R}^2,\ (x+y)^2=x^2+2xy+y^2,\] d'une définition d'un nouvel objet mathématique comme \(E:=\{a,b\}\) qui permet de baptiser \(E\) la paire \(\{a,b\}\). Dans notre pseudo-langage algorithmique nous utiliserons la flèche à gauche \(\leftarrow\) lar­ge­ment répandue également.

Mais revenons à notre problème. La première difficulté est que la structure de chaîne de caractères commence son indexation à 0 et non à 1 comme nous l'avons fait dans l'algorithme. L'impact n'est pas anodin, le résultat de l'exercice 1 qui nous a permis de prouver que l'algorithme était juste suppose que l'indice \(i\) appartient à l'intervalle \([1,n]\) et non à l'intervalle \([0,n-1]\). L'adaptation sans analyse mathématique préalable peut s'avérer périlleuse et occasionne une perte de temps con­si­dé­ra­ble en développement. Ici les inégalités larges des tests initiaux ont été remplacées par des inégalités strictes. Le double \(//\) désigne le quotient de la division euclidienne, il s'agit donc bien de la partie entière de \(\frac{n}{2}\).

Un danger plutôt pervers se cache dans la condition (i < n) and (u[i] == v[i]) de la boucle while de la première fonction. L'écriture de cette condition est parfaitement naturelle puisqu'elle ne fait que transposer ce que nous ferions à la main, à savoir tant que l'on n'a pas atteint la fin du mot et que les lettres sont identiques, on avance. Ces notions d'analyse le­xi­ca­le et syn­ta­xi­que se­ront étu­diées en détail dans le cours de théorie des langages et com­pi­la­tion en troisième année. Il n'est pas certain qu'un programme informatique évalue une expression comme le ferait un être humain et ceci peut poser quelques problèmes. Dans l'évaluation d'une expression, une première phase consiste à faire une analyse lexicale et à segmenter la chaîne de caractères en unités lexicales (jetons), constantes, opérateurs, identificateurs, etc.

Les unités lexicales sont ensuite rangées dans un arbre syntaxique :

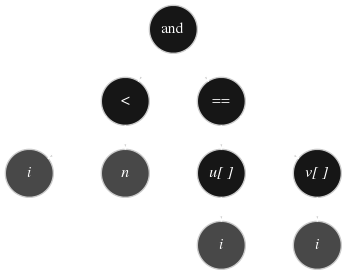
Arbre syntaxique (simplifié) de l'expression logique \((i < n)\ \text{and}\ (u[i]==v[i])\).

Chaque opérateur est rangé dans un nœud de cet arbre binaire dont les fils sont ses opérandes (le nombre de fils correspond à l'arité de l'opérateur). Ici nous sommes en présence d'opé­ra­teurs binaires (\( < \) ou \( == \) par exemple) et unaire (\([\ ]\)). Le procédé est éminemment récursif, si un opérande est lui même une expression, son nœud devient la racine du sous-arbre qui la représente etc. Cet arbre est ensuite évalué récursivement, chaque nœud est alors remplacé par le résultat de l'opération.

On voit poindre le problème potentiel. En soi, l'expression logique \((i < n)\wedge (u_i=v_i)\) n'a aucune dimension temporelle et on pourrait permuter les deux opérandes de la conjonction, soit l'expression \((u_i=v_i) \wedge (i < n)\), sans que cela change quoi que ce soit à sa valeur logique. Néanmoins, nous lisons de la gauche vers la droite et nous savons que la valeur de vérité d'une expression de la forme \(P_1\wedge P_2\wedge\cdots\wedge P_n\) est fausse dès qu'un \(P_i\) est faux sans qu'il soit nécessaire d'évaluer les \(P_k\) pour \(k>i.\) A priori, rien n'indique comment l'arbre syntaxique va être évalué, il est même envisageable qu'il soit évalué dans son intégralité ce qui invaliderait l'algorithme puisqu'une fois que l'indice \(i\) atteint la valeur \(n\), la quantité \(u[i]\) n'est plus définie. Fort heureusement, les compilateurs et interprètes mo­der­nes évaluent les expressions comme nous imaginons qu'ils doivent le faire, mais il est préférable d'écrire des programmes robustes. À cette fin, on peut réécrire la fonction #1 de la manière sui­van­te : 

def Est-Palindrome-Bis(u):
    n = len(u)
    v = ""
    i = 0
    while (i < n):
        v = u[i] + v
        i = i + 1
    i = 0
    OnContinue = True;
    while (i < n) and OnContinue:
        OnContinue = (u|i] == v[i])
        i = i + 1
    return (i >= n)

L'algorithme peut s'écrire de manière extrêmement concise en Python à l'aide de l'opé­ra­teur d'indexation (les crochets) : 
def Est-Palindrome-Ter(u):
    return u == u[::-1]
Cette écriture, aussi séduisante soit-elle pour le développeur pressé, a pour défaut majeur de cacher le nombre d'opérations exécutées par l'interprète Python pour évaluer l'expression et par con­sé­quent laisse accroire au programmeur débutant que ces questions ne sont pas essentielles. Nous y re­vien­drons dans le chapitre consacré à la complexité.