Vous trouverez sur cette page une brève introduction à la machine de Turing et un simulateur qui vous permettra de mettre à l'épreuve votre compréhension du modèle en testant vos propres pro­gram­mes.

Introduction

La machine de Turing est un modèle de machine abstrait introduit en 1936 par le chercheur anglais Alan Turing dans un article fondateur intitulé On Computable Numbers, With An Application To The Entscheidungsproblem dans lequel il propose une réponse à une question posée 8 ans plus tôt par le célèbre mathématicien David Hilbert. Il s'agit du problème de la décidabilité (en allemand "Entscheidungsproblem") soit en substance: existe-t-il un algorithme qui décide si une proposition énoncée dans un système logique est valide ou non ?

Pourquoi le modèle de calcul proposé par Alan Turing est-il devenu un outil indispensable en in­for­ma­ti­que fondamentale et en mathématiques ? Sa machine est en effet largement utilisée en théorie de la calculabilité, en théorie de la complexité ou en théorie de l'approximation. La raison principale tient à son extrême simplicité qui a permis d'établir des résultats sans nul doute beaucoup plus difficiles à démontrer avec des modèles moins rudimentaires. Cette machine est en fait le modèle le plus simple que l'on puisse concevoir et qui satisfait aux critères informels mais universels qui caractérisent un algorithme (déterminisme, discrétion, finitude, généralité, etc.)

Il faut noter que ce modèle, comme tant d'autres, a vu le jour à une époque où les ordinateurs tels que nous les connaissons aujourd'hui n'existaient pas, il s'agit donc avant tout d'un outil abstrait. La généralisation des ordinateurs dans les années 50-60 a donné naissance au modèle ram (Register Addressable Memory), plus proche de leur architecture physique et logique. Ce qui est remarquable, c'est que l'on a pu démontrer que tous ces modèles étaient équivalents, ce que l'on peut calculer avec le modèle A peut l'être avec le modèle B et réciproquement.

Il est communément admis que tout modèle abstrait de calcul respectant les conditions informelles sur lesquelles les scientifiques s'accordent pour parler d'algorithme (si l'on excepte le calcul quan­ti­que qui définit un nouveau paradigme) aboutit à un modèle équivalent aux précédents. Ce résultat, appelé thèse de Church-Turing Alonzo Church est un ma­thé­ma­ti­cien américain in­venteur d'un autre mo­dè­le appelé λ-calcul ne peut évidemment pas être démontré puisque le concept d'al­g­ori­thme est un concept informel. Un des objectifs du cours est de montrer l'équivalence des modèles de Turing et ram.

Il faut garder à l'esprit que la machine de Turing est un modèle universel de calcul et qu'elle peut calculer tout ce que n'importe quel ordinateur physique peut calculer (aussi puissant soit-il). In­ver­sement, ce qu'elle ne peut pas calculer ne peut l'être non plus par un ordinateur. Elle résume donc de manière saisissante le concept d'ordinateur et constitue un support idéal pour raisonner autour de la notion d'algorithme de calcul ou de démonstration.

Présentation de la machine.

Il existe différentes formulations de la machine de Turing, les deux que nous allons présenter ici correspondent aux plus courantes. En guise d'exercice d'application du cours, vous pourrez dé­mon­trer que ces deux modèles sont équivalents en terme de calculabilité.

Pour reprendre l'idée même d'Alan Turing, sa machine n'est rien d'autre qu'une version minimaliste de la machine à écrire que l'on pourrait contrôler à l'aide d'un programme. Une machine à écrire peut écrire ou effacer un symbole sur la feuille (même si l'effacement mécanisé avec un ruban correcteur n'était pas présent sur les premiers modèles), avancer ou reculer d'un ou plusieurs caractères. Au lieu d'opérer en deux dimensions sur une feuille de papier, la machine de Turing se contente d'une bande infinie à gauche et à droite et segmentée en cellules pouvant contenir chacune un symbole. Une tête de lecture/écriture remplace les barres à caractère physiques et agit sur la bande en suivant les règles du programme. Par commodité, on indexe souvent les cases de cette bande avec l'ensemble des entiers relatifs Z.

La bande joue à la fois le rôle de périphérique d'entrée et de sortie. Initialement vierge, on y inscrit à la main (virtuellement, c'est un modèle abstrait !) les données à traiter par le programme (entrée), qui sont des mots sur un alphabet Σ arbitraire mais fini. Par convention, on sépare les mots par une cellule vide et le premier symbole du premier mot est placé dans la cellule d'indice 0 où se trouve la tête de lecture/écriture. Pendant l'exécution du programme, la tête de lecture/écriture peut se déplacer à gauche ou à droite, lire le contenu de la cellule sur laquelle elle se trouve, l'effacer ou y écrire un symbole de Σ. À la fin de l'exécution du programme, les mots sur la bande constituent le résultat du calcul (sortie).

Le fonctionnement est discret et ce que réalise la machine à chaque étape ne dépend que de deux paramètres : le symbole lu, c'est-à-dire celui qui est situé dans la cellule sur laquelle est placée la tête de lecture/écriture (le symbole \(t\) dans l'exemple ci-dessus), et l'état de la machine. Pour contrôler la machine, le programmeur dispose d'un ensemble fini d'états \(Q\) de son choix. Il fixe également l'état initial. C'est le programme qui va déterminer ce que la machine va faire en fonction du couple \((p,s)\) constitué par l'état courant de la machine et le symbole lu. Si la cellule est vide, on considère que le symbole lu est un symbole particulier appelé "blanc" et noté \(\square\).

Une première description du programme

"Si la machine est dans l'état \(\color{yellow}p\) et que le symbole lu est \(\color{yellow}s\) (i.e. la case sous la tête de lecture/écriture contient le symbole \(s\)), alors la machine exé­cute l'opé­ra­tion \(\color{#88F}\omicron\) et passe dans l'état \(\color{#88F}q\).

1. Écriture : si \(\omicron\in\Sigma\), le contenu de la cellule est écrasé par le symbole \(\omicron\) ;
2. Effacement : si \(\omicron=\square\), le contenu de la cellule est effacé ;
3. Déplacement : si \(\omicron\in\{\leftarrow,\rightarrow\}\), la tête de lecture/écriture se déplace vers la cellule à gauche ou à droite respectivement.

Une deuxième description du programme

"Si la machine est dans l'état \(\color{yellow}p\), et que le symbole lu est \(\color{yellow}s\) (i.e. la case sous la tête de lecture/écriture contient le symbole \(s\)), alors elle écrit/efface selon \(\color{#88F}e\), se déplace selon la direction \(\color{#88F}d\) et son nouvel état est \(\color{#88F}q\)."

1. Écriture : si \(e\in\Sigma\), le contenu de la cellule est écrasé par le symbole \(e\) ;
2. Effacement : si \(e=\square\), le contenu de la cellule est effacé ;
3. Déplacement : selon que \(d=\leftarrow\) ou \(d=\rightarrow\), la tête de lecture/écriture se déplace vers la cellule à gauche ou à droite respectivement.

On rajoute parfois dans la définition un septième ensemble \(T\subseteq\Gamma\) dit des états terminaux ou finaux, c'est-à-dire des états dans lesquels la machine peut se trouver quand elle a fini son exécution. Ceci peut-être utile pour reconnaître des langages à la manière des automates. Par exemple, dans le cas de problèmes de décision, on définira classiquement \(T:=\{q_Y,q_N\}\), et on dira que \(q_Y\) est l'état d'acceptation et \(q_N\) est l'état de rejet. Le simulateur simule les deux modèles, le modèle à simuler étant déterminé automatiquement par la nature des règles contenues dans le fichier programme.

Définitions

Il devient clair à présent que le programme d'une machine de Turing n'est rien d'autre que le graphe de sa fonction de transition \(\delta\). C'est par simple commodité pour écrire les programmes que l'on écrit \(p,s:o,q\) plutôt que \(\delta(p,s)=(o,q)\). D'où la définition:

Une bande \(B\) se modélise simplement, il s'agit d'un élément de \(\Gamma^{\mathbf Z}\), il est donc commode de désigner par \(B[k]\), à la manière des listes où des tableaux, le contenu de la cellule d'indice \(k\) (qui ici peut être négatif). Compte tenu des conventions établies pour l'utilisation de la machine de Turing, à chaque instant entre deux transitions, la bande est nécessairement vide de part et d'autre d'une zone utile, c'est-à-dire \begin{equation*} \exists (g,d)\in{\mathbf Z}\times{\mathbf Z},\ \ \forall i\in {\mathbf Z},\quad (i < g)\vee(i > d)\Rightarrow B[i] = \square \end{equation*} on représente donc son contenu par le mot de \(\Gamma^*\) constitué par la suite des symboles contenu dans les cellules d'indices \(g\) à \(d\) que l'on identifie au sous-tableau \(B[g\!:\!d]\). On peut alors définir ce qu'est une configuration.

Avec les conventions établies, avant l'exécution d'un programme et avant que l'utilisateur n'ait saisi le mot d'entrée, la configuration de la machine est donc le quadruplet \((q_0,\epsilon,0,0)\) où \(\epsilon\) désigne le mot vide de \(\Gamma^*\). Une fois le mot \(u\in\Gamma^*\) saisi, la configuration est alors \((q_0,u,0,0)\).

Le diagramme des transitions permet de représenter graphiquement la fonction de transition. Il s'agit d'un multigraphe dont les sommets sont les états de la machine et les arcs représentent les transitions entre deux états. Les arcs sont étiquettés par le symbole lu et l'opération réalisée. Chaque machine ci-dessous est accompagnée de son diagramme des transitions. Le simulateur fournit ce diagramme au format dot de Graphviz une fois que le fichier programme a été chargé.

Exemples de programmes

Tous les programmes fournis ici peuvent être chargés puis exécutés sur ce simulateur écrit en javascript (et en php pour la lecture du fichier programme). Quand nous utiliserons l'alphabet unaire \(\Sigma=\{!\}\), l'unique symbole de Σ appelé bâton est représenté par un point d'exclamation. Dans ce cas l'ensemble des entiers naturels \({\mathbf N}\) est identifié au langage \(\Sigma^+\) grâce à la bijection \(\varphi:{\mathbf N}\rightarrow\Sigma^+\) définie par \(\varphi(n) :=\; !^{n+1}\) où la notation exponentielle est associée à l'opérateur de concaténation, par exemple \(!^3=\; !!!\) et \(!^0=\epsilon\), le mot vide.

Doubler le nombre de bâtons

Fichier source.

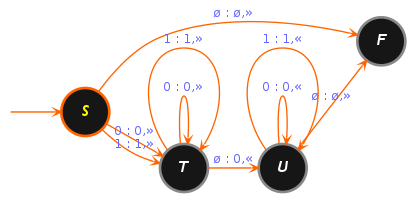
Avec l'identification que nous nous sommes fixée entre N et Σ⁺, la machine calcule donc la fonction n ↦ 2n + 1. Initialement, la tête de lecture/écriture est sur le bâton le plus à gauche de la séquence initiale notée u = !^k. Le principe général consiste à effacer successivement tous les bâtons de u par la gauche et pour chaque bâton effacé d'en rajouter deux à une séquence v initialement vide.

Plus précisément, la bande contient initialement □^∞!^k□^∞. On efface le premier bâton de u, et on l'écrit au bout de la séquence v initialement vide et située à gauche de la séquence u. La bande contient alors □^∞!□!^{k - 1}□^∞. On parcourt tous les bâtons de v vers la gauche (à cette étape v n'en contient qu'un) et on inscrit le second bâton au début de v. La bande contient donc □^∞!!□!^{k - 1}□^∞. On se replace à gauche de la séquence u qui ne contient plus que k - 1 bâtons et on recommence jusqu'à ce que tous les bâtons de u soient effacés. Le programme suivant réalise ces opérations:

Diagramme des transitions de cette machine.

Fonction définie par n ↦ (n,n)

Fichier source

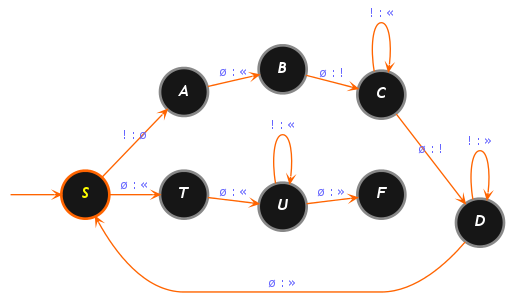
L'algorithme consiste à initialiser à un bâton une séquence v à gauche de u en séparant v et u par une cellule vide. Puis on efface un à un les n premiers bâtons de la séquence u qui en contient initialement n + 1. Pour chaque bâton effacé de u, on le rajoute à gauche de v. Une fois qu'il ne reste plus que le dernier bâton à la séquence u, on remplit les n + 1 cellules vides séparant v et u, on recrée la cellule séparatrice pour arriver finalement à □^∞!^k□!^k□^∞.

Diagramme des transitions de cette machine.

Calculer la fonction de définie par (a,b) ↦ a + b. (addition)

Fichier source.

Entrée: Une séquence de k := a + 1 bâtons suivie d'une séquence de l := b + 1 bâtons.
Sortie: Une séquence de a + b + 1 bâtons.

L'algorithme est extrêmement simple, la bande contient initialement □^∞!^k□!^l□^∞ et il suffit de placer le symbole ! dans la cellule vide qui sépare les deux séquences de k batôns et de l bâtons (□^∞!^k+l+1□^∞) et d'effacer les deux bâtons à gauche de la séquence de k + l + 1 bâtons ainsi constituée.

Diagramme des transitions de cette machine.

Calculer la fonction définie par (a,b) ↦ a × b. (produit)

Fichier source.

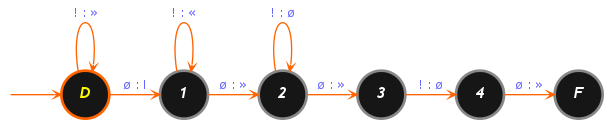
Entrée: Une séquence de k := a + 1 bâtons suivie d'une séquence de l := b + 1 bâtons.
Sortie: Une séquence de a × b + 1 bâtons.

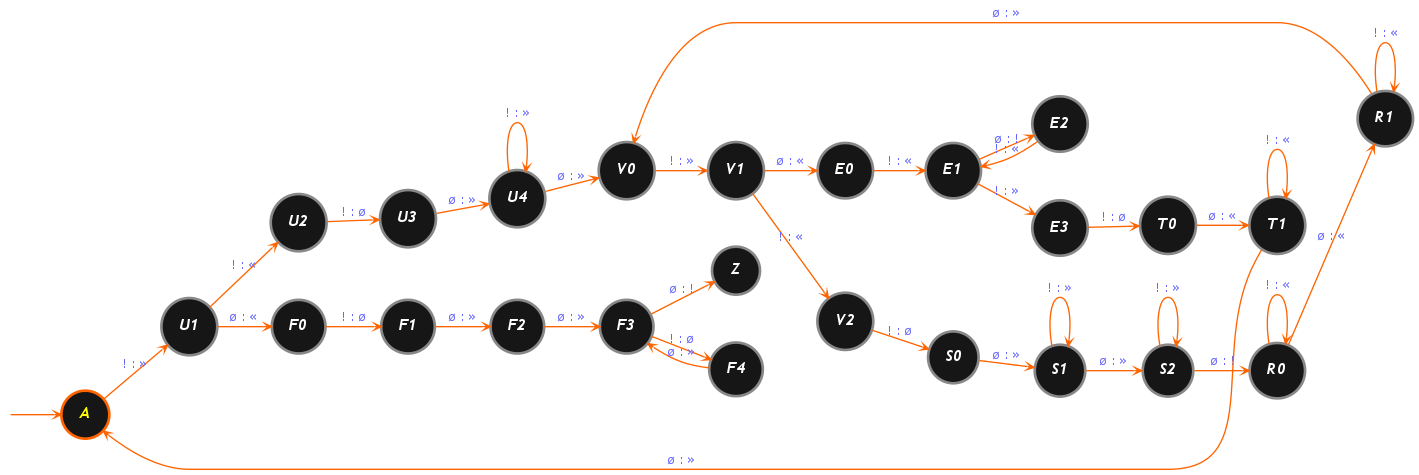
L'algorithme consiste, pour chacun des a premiers bâtons de la première séquence u (qui en contient a + 1 au départ), de recopier les b premiers bâtons de la seconde séquence v (qui en contient b + 1 au départ) au bout d'une troisième séquence w initialement vide. Cette copie se fait en effaçant successivement les b premiers bâtons de v et en les recopiant au bout de w, le dernier bâton de v sert à contrôler la fin de la copie après laquelle on reconstitue les b bâtons effacés pendant la copie. Une fois qu'il ne reste qu'un bâton à u, la séquence w en contient a × b, on peut alors terminer. On efface le dernier bâton de u ainsi que les b + 1 bâtons de v et on rajoute un dernier bâton à la séquence résultat w.

Diagramme des transitions de cette machine.

Décider si un entier est multiple de 4.

Fichier source.

Entrée: un entiers n en binaire.
Sortie: Oui/Non. La réponse est fournie par l'état d'arrêt de la machine.

Cette fois nous utilisons le deuxième modèle de machine de Turing comme une machine décisionnelle, les états d'acceptation q_Y et de refus q_N sont tous simplement représentés par les chaînes "OUI" (l'entier est multiple de 4) et "NON" (l'entier n'est pas multiple de 4) dans le programme. On suppose que l'alphabet est binaire, i.e. Σ :={0,1}.

Initialement, la tête de lecture/écriture doit être sur le bit de poids fort de n. Le principe est simple, pour que n soitmultiple de 4, il faut et il suffit que ces deux derniers bits de poids faible soient égaux à 0.

Diagramme des transitions de cette machine.

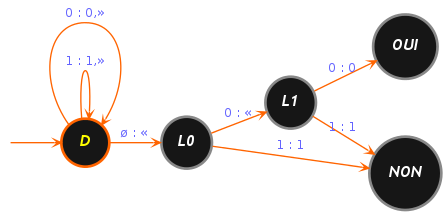
Multiplier par 2 un entier représenté en binaire

Fichier source.

Nous utilisons encore le deuxième modèle de machine de Turing. On suppose que l'alphabet est binaire, i.e. Σ :={0,1}. Il suffit de rajouter un 0 après le bit de poids faible de n.

Diagramme des transitions de cette machine.