Tri par tas - Algorithmique II

La notion de graphe a été abordée en 1ère année et ses nombreuses déclinaisons s'avèrent d'une très grande richesse, à la fois comme modèles et comme outils d'étude en algorithmique. Elle fait l'objet d'une théorie à part entière, la théorie des graphes.

Un graphe orienté est un couple \((X,U)\) où \(X\) est un ensemble de sommets et \(U\subseteq X\times X\) est l'ensemble des arcs.

Dans un arc \((x,y)\), le sommet \(x\) est appelé le prédécesseur de \(y\) et \(y\) le successeur de \(x\). On note \(\Gamma\) la correspondance \((X,U,X)\) et pour tout sommet \(x\in X\) du graphe, on écrira \(\Gamma(x)\) (resp. \(\Gamma^{-1}(x)\)) plutôt que \(\Gamma(\{x\})\) (resp. \(\Gamma^{-1}(\{x\})\)) l'ensemble des successeurs (resp. prédecesseurs) de \(x\). Un arc \((x,x)\) est appelé une boucle. Un graphe orienté hérite du vocabulaire d'un graphe d'une relation binaire, réflexif, symétrique, transitif, etc. Si l'orientation n'a pas d'importance, on remplace généralement les couples par des paires \(\{x,y\}\) ou des singletons \(\{x\}\) pour les boucles, i.e. \(U\subseteq({\mathscr P}_2(X)\cup{\mathscr P}_1(X))\). On parle alors d'arête au lieu d'arc et le graphe est dit non orienté.

Dans un graphe orienté (resp. non orienté), une séquence \(x_1x_2\ldots x_n\) de \(n\) sommets telle que \(\forall i\in\ab{1}{n-1}\ (x_i,x_{i+1})\in U\) du graphe est appelée un chemin (resp. une chaîne) reliant \(x_1\) à \(x_n\). Si la séquence commence et se termine par le même sommet, i.e. \(x_1=x_n\), on parle de circuit (resp. de cycle). Un chemin/chaîne qui passe exactement une fois par chaque arc/arête est appelé chemin eulérien/chaîne eulérienne. Un chemin/chaîne qui passe exactement une fois par chaque sommet est appelé chemin hamiltonien/chaîne hamiltonienne.

Les termes chaîne et cycle peuvent s'appliquer à une séquence de sommets d'un graphe orienté si l'on ne tient pas compte de l'orientation des arcs.

Un graphe est dit connexe si pour tout couple de sommets du graphe, il existe au moins une chaîne qui les relie (on ne tient compte que de la connexion, pas du sens des flèches). La longueur d'un chemin (resp. d'une chaîne) est le nombre de ses arcs (resp. de ses arêtes). Un sous-graphe d'un graphe \(G=(X,U)\), c'est-à-dire la restriction de ses arcs/arêtes à un sous-ensemble \(Y\) de \(X\), est appelé composante connexe de \(G\) s'il est connexe et maximal : aucune chaîne ne relie un sommet de \(X\setminus Y\) à un sommet de \(Y\). Un sous-graphe est appelé composante fortement connexe si pour tout couple de sommet \((x,y)\) il existe un chemin qui relie \(x\) à \(y\) (là on tient compte du sens des flèches). Comme l'orientation n'importe pas dans un graphe non orienté, s'il est connexe il est fortement connexe.

Un arbre \(A\) est un graphe \((X,U)\) connexe et sans cycles. Le sommet d'un arbre est appelé un nœud et un arc est appelé une branche.

Un nœud qui n'a pas de fils est appelé une feuille. Un arbre enraciné est un arbre dans lequel il existe un unique nœud qui n'a pas de prédécesseur, on l'appelle la racine de l'arbre. On démontre qu'il existe une unique chaîne qui relie deux nœuds quelconques d'un arbre et que dans un arbre enraciné, tout nœud différent de la racine admet un seul père.

La profondeur d'un nœud ou la hauteur d'un nœud (tout est question de point de vue…) est la longueur du chemin qui le relie à la racine de l'arbre. La profondeur d'un arbre est la profondeur maximale d'une feuille. Le nombre de nœuds à la profondeur \(p\) est au plus \(q^p\) si l'arbre est d'arité \(q\). Un arbre de profondeur \(p\) est dit équilibré si tout nœud de profondeur \(k\) tel que \(k < p - 1\) a exactement \(q^k\) fils. Un arbre peut être muni d'une valuation de ses nœuds (et/ou de ses arcs), c'est-à-dire d'une application \(\nu:X\to{\mathbb R}\) (et/ou \(\mu:U\to{\mathbb R}\)).

Dans un arbre, deux nœuds quelconques sont toujours reliés par une unique chaîne, i.e. ces deux nœuds sont aux extrémités opposées de cette chaîne.

On cherche à nouveau à trier les valeurs d'un tableau/liste dans l'ordre croissant. Le tri par tas repose sur des échanges de valeurs des nœuds d'un arbre binaire valué. Bien que les arbres soient indispensables pour comprendre ces manipulations, ce tri n'utilise jamais de structure d'arbre pour son implantation, mais opère in situ, c'est-à-dire sur le tableau/liste fourni(e) en entrée.

L'algorithme s'appuie sur une propriété particulière de certains tableaux appelés tas. Pour comprendre ce qu'est un tas, il faut introduire la notion d'arbre partiellement ordonné (en résumé APO).

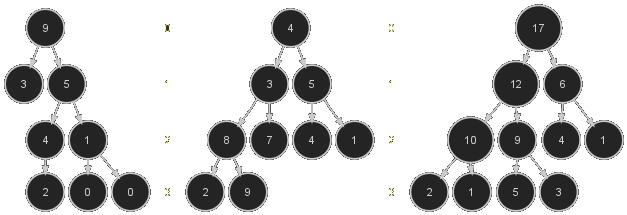
Un arbre \(A = (X,U)\) muni d'une valuation de ses nœuds \(\nu\) est appelé arbre partiellement ordonné si et seulement si \begin{equation}\label{eq:apo} \forall x \in X\ \ \forall y\in\Gamma(x)\quad \nu(x) \geq \nu(y). \end{equation}

Dans les arbres ci-dessous, l'arbre binaire à gauche est partiellement ordonné mais pas équilibré, l'arbre central est équilibré mais n'est pas partiellement ordonnée, tandis que l'arbre à droite est à la fois équilibré et partiellement ordonné. Les nombres entre les arbres indiquent la profondeur des nœuds dans l'arbre. Notons que les arbres sont représentés à l'envers (racine en haut et feuilles en bas) à cause du sens de lecture qui suit la chronologie de leur construction, celle-ci commençant très souvent par la racine (pour le modèle abstrait tout au moins).

Quand on dispose d'un arbre équilibré valué, on peut le représenter très simplement avec une structure de liste/tableau et réciproquement, il suffit de ranger les valuations des nœuds dans la liste en suivant l'ordre naturel de lecture, de la gauche vers la droite et de haut en bas. Ainsi le tableau associé à l'arbre de droite de la figure ci-dessus est \begin{equation}\label{ex:tas} T = [17,12,6,10,9,4,1,2,1,5,3] \end{equation}

La propriété APO a pour conséquence immédiate que la racine de l'arbre contient la valeur la plus grande, autrement dit la première valeur du tableau est la plus grande. Cette propriété est la clef du fonctionnement du tri par tas. Ce tri ne manipule en réalité qu'une structure de tableau/liste et jamais de structure d'arbre qui ne sert qu'à comprendre les mécanismes de ce tri. Nous allons tout d'abord décrire comment l'algorithme trie un tas. Bien entendu tous les tableaux ne sont pas des tas, mais nous verrons comment transformer un tableau quelconque en tas avec l'algorithme Entasser un peu plus bas.

Le principe est simple et élégant. La plus grande valeur, \(17\) dans notre exemple, étant placé en tête du tas d'après le lemme précédent, il suffit de l'échanger avec la dernière valeur du tableau, ici \(3\), pour qu'elle soit définitivement rangée comme le fait le TriSélection. C'est ce que montre l'arbre de gauche ci-dessous pour le tas \((\ref{ex:tas})\). Après cette transposition, l'arbre n'est plus nécessairement apo (sauf si la valeur qui était dans la dernière cellule du tableau avant l'échange se trouvait être justement la seconde plus grande valeur du tableau).

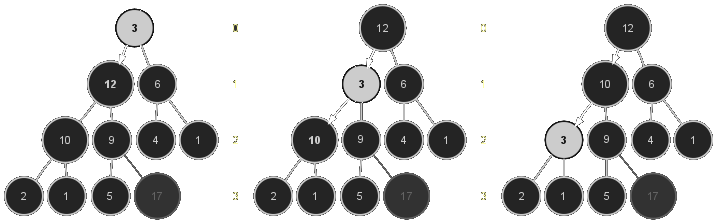
Restauration de la propriété APO par l'algorithme Tamiser de \(T = [17,12,6,10,9,4,1,2,1,5,3]\) après échange des valeurs \(3\) et \(17\).

Pour restaurer la propriété APO à la racine, il suffit d'échanger sa valeur avec celle du fils qui contient la plus grande, ici \(12\) (cf. arbre au centre de la figure). On repousse alors le problème sur la racine du sous-arbre où l'on a fait l'échange, ici le sous-arbre gauche, et il suffit de recommencer l'opération jusqu'à ce que la propriété soit rétablie, au pire en rencontrant une feuille. Dans notre exemple, la valeur 3 s'arrête dans sa descente après la transposition avec \(10\) puisque la propriété apo est alors vérifiée. L'opération qui consiste à faire descendre la valeur de la racine dans l'arbre doit bien entendu être réalisée sur le tableau T. Le lecteur démontrera le lemme suivant :

Soit \(i\) l'index d'un nœud d'un arbre binaire équilibré associé à un tableau indexé de \(1\) à \(n\). Alors :

l'index du fils gauche, s'il existe, est égal à \(2i\),
l'index du fils droit, s'il existe, est égal à \(2i+1\),
l'index du père, s'il existe, est égal à \(\lfloor\frac{i}{2}\rfloor\).

L'algorithme Tamiser a trois paramètres, le tableau, l'index du père et l'index de la dernière cellule à considérer dans le tableau. Les premières instructions #13 à 15) de l'algorithme servent à trouver la valeur k de l'indice du fils avec lequel il faudra faire l'échange, c'est-à-dire le plus grand des deux fils.

Le troisième paramètre de l'algorithme peut sembler superflu mais sera nécessaire pour faire le tri. L'algorithme renvoie un booléen indiquant si oui ou non il y a eu échange. La preuve du résultat suivant qui justifie la validité de l'algorithme est laissée au lecteur.

Soit \(A=(X,U)\) un arbre binaire dont les sous-arbres gauche et droit sont des APO. Alors, l'arbre obtenu après l'application de l'algorithme Tamiser à sa racine est un APO.

Le tri d'un tas coule alors de source, l'arbre ayant retrouvé sa propriété APO, la plus grande valeur du tableau est de nouveau en première position et il suffit de l'échanger avec l'avant dernière valeur et de recommencer le processus jusqu'à ce que toutes les plus grandes valeurs aient été rangées à la fin du tableau. Supposons que l'on dispose d'un algorithme Entasser (nous le décrirons plus loin) qui transforme un tableau quelconque en tas, le tri s'écrit facilement:

Il reste à présent à convertir un tableau quelconque \(T\) en tas. Pour celà, il faut rétablir la propriété \((\ref{eq:apo})\) en chaque nœud où elle fait défaut. C'est bien sûr l'algorithme Tamiser qui va être appliqué sur les nœuds en question. On pourrait être tenté de traiter les nœuds dans l'ordre de lecture, donc en commençant par la racine de l'arbre, mais le tableau \(T=[1,3,2,4]\) est transformé en \(T=[3,4,2,1]\) par l'algorithme et ce n'est pas un tas. Le lemme 8 indique comment procéder. En commençant par le bas, on s'assure ainsi que les sous-arbres gauche et droit sont toujours APO avant d'appliquer l'algorithme. Comme les feuilles sont toujours APO, il est inutile de les tester. Reste alors à déterminer par quel nœud commencer ?

Dans un tableau de taille \(n\) et de premier indice 1 associé à un arbre binaire équilibré, le plus grand indice du nœud qui n'est pas une feuille est égal à \(\lfloor\frac{n}{2}\rfloor\).

Nous allons estimer la complexité en calculant le nombre de fois où l'on teste la propriété APO qui est la clef du fonctionnement des deux algorithmes, Entasser et TriTas. Ce nombre de tests permet aisément de déterminer le coût global puisque si la condition apo est satisfaite il n'y a rien à faire, sinon il faut échanger un père avec l'un de ses fils, mais dans les deux cas le coût est constant. Donc chaque test de condition apo a une complexité en \(\Theta(1)\).

En notant \(n:=\#T\) et \(\tau(i)\) le nombre de tests apo réalisés par Tamiser(T,i,n) dans la boucle, le nombre total de tests est \[ \sum_{i=\lfloor\frac{n}{2}\rfloor}^{1}\tau(i). \] Dans le meilleur des cas le tableau est déjà un tas et un seul test a lieu pour chacun des \(\lfloor\frac{n}{2}\rfloor\) à traiter, i.e. \(\tau(i)=1\), on a donc \[ \check T_{\text{Entasser}}(n)=\Theta(n). \]

Démontrez qu'un nœud d'indice \(i\) est à la profondeur \(\lfloor \log_2 i\rfloor\). En déduire la hauteur \(h\) d'un arbre binaire équilibré à \(n\) sommets.

Mais la définition d'une partie entière nous donne les inégalités \[ \lfloor \log_2 i\rfloor\leq \log_2 i \lt \lfloor\log_2 i\rfloor + 1, \] et on déduit \(-\lfloor \log_2 i\rfloor \lt 1-(\log_2 i) \) de la dernière pour obtenir \begin{align} \hat T_{\text{Entasser}}\;(n) &\leq \lfloor\frac{n}{2}\rfloor (h+1)+\sum_{i=1}^{\lfloor n/2\rfloor}(1-(\log_2 i))\\ &\leq \lfloor\frac{n}{2}\rfloor (\log_2 n+2)-\sum_{i=1}^{\lfloor n/2\rfloor}\log_2 i\\ &\leq \lfloor\frac{n}{2}\rfloor\log_2 n + n-{\color{yellow}\sum_{i=1}^{\lfloor n/2\rfloor}\log_2 i}\label{eqtas}\quad\text{car}\ 2\lfloor\frac{n}{2}\rfloor\leq n. \end{align} Classiquement, on minore la somme par une intégrale en se rappelant qu'une primitive de \(\ln x\) est \(x\,\ln x -x\) : \begin{align}\label{eq:majint} {\color{yellow}\sum_{i=1}^{\lfloor n/2\rfloor}\log_2 i}= \sum_{i=2}^{\lfloor n/2\rfloor}\log_2 i &\geq\frac{1}{\ln 2}\int_{1}^{\lfloor n/2\rfloor}\ln x\, dx\\ &\geq\frac{1}{\ln 2}\left[x\ln x -x\right]_{1}^{\lfloor n/2\rfloor}\\ &\geq\frac{1}{\ln 2}\left(\lfloor\frac{n}{2}\rfloor\ln\lfloor\frac{n}{2}\rfloor-\lfloor\frac{n}{2}\rfloor+1\right)\\ &\geq \lfloor\frac{n}{2}\rfloor \log_2\lfloor\frac{n}{2}\rfloor - \frac{1}{\ln 2}(\lfloor\frac{n}{2}\rfloor-1)\\ &\geq \lfloor\frac{n}{2}\rfloor \log_2\lfloor\frac{n}{2}\rfloor - 2(\lfloor\frac{n}{2}\rfloor-1)\quad\text{car}\ 1/(\ln 2)<2 \\ &\geq \lfloor\frac{n}{2}\rfloor \log_2\lfloor\frac{n}{2}\rfloor - 2\lfloor\frac{n}{2}\rfloor \\ &\geq \lfloor\frac{n}{2}\rfloor \log_2\lfloor\frac{n}{2}\rfloor - n \end{align} En injectant ce résultat dans (\ref{eqtas}) : \begin{align} \hat T_{\text{Entasser}}\;(n) &\leq \lfloor\frac{n}{2}\rfloor\log_2 n + n-\color{yellow}{\lfloor\frac{n}{2}\rfloor \log_2\lfloor\frac{n}{2}\rfloor +n}\\ &\leq \lfloor\frac{n}{2}\rfloor\left(\log_2n-\log_2\lfloor\frac{n}{2}\rfloor \right)+2n\\ &\leq \underbrace{\lfloor\frac{n}{2}\rfloor\left(\log_2n-\log_2\lfloor\frac{n}{2}\rfloor \right)+2n}_{f(n)} \end{align}

Si \(n\) est pair, disons \(n=2k\), on vérifie que \(f(2k)=5k\) et donc \(f(n)=\frac{3n}{2}\). Comme \(f\) est croissante, \(f(n)\leq f(n+1)\) et si \(n=2k+1\), alors \(f(n)\leq 5(k+1)=\frac{5}{2}(n+1)\). On en conclut que \[\hat T_{\text{Entasser}}(n)=O(n).\]

L'analyse du meilleur des cas et du cas moyen sont très difficiles et n'ont été obtenus qu'en 1992 par R. Shaeffer et R. Sedgewick et publiés dans The analysis of heapsort, Journal of Algorithms, Vol. 15, #1, pp. 76-100, 1993. Dans les deux cas la complexité est en \(\Theta(n\log n)\) mais le cas moyen est 2 fois plus coûteux que le meilleur des cas.

Attention ! En \(C\) les indices des tableaux commencent à \(0\), il faut donc adapter toutes les formules des algorithmes.

Écrivez une fonction void Tamiser(int *T,uint i,uint n) qui applique l'algorithme de descente du nœud d'indice i dans le sous-arbre associé au sous-tableau T[1,n].

Écrivez une fonction void Entasser(int *T, uint n) qui transforme un tableau quelconque en tas. Écrivez une fonction void TriTas(int *T, uint n) qui trie un tableau T à l'aide du tri par tas en utilisant les deux fonctions écrites précédemment.

Vérifiez de manière empirique que la fonction de complexité de l'algorithme du tri par tas dans le cas moyen est \(\hat T(n)=\Theta(n\log n)\). Pour cela, comparez les graphes des fonctions suivantes à l'aide de Gnuplot : la fonction du nombre de comparaisons (uniquement celles liées à l'arbre de décision) selon la taille \(n\) de la liste à trier et la fonction \(n\mapsto n\log n\).

Pour cela, reprenez la fonction uint *GenPerm(uint n) qui renvoie une permutation de taille \(n\) dont les valeurs ont été tirées au hasard. Reprenez cette suggestion pour engendrer une permutation aléatoire.