Notations asymptotiques

Généralités

C'est l'étude des fonctions de complexité des algorithmes qui nous amène à introduire des outils d'analyse efficaces et c'est leur comportement asymptotique qui nous éclaire sur les temps de calculs que l'on peut espérer une fois qu'ils seront implantés sur des ordinateurs. Plutôt que calculer l'expression exacte de la fonction de complexité, qui reste souvent hors de portée, on cherche surtout à déterminer son comportement général. La fonction est-elle de type logarithmique, linéaire, linéa­ri­thmi­que, quadratique, exponentielle, etc. ?

Le domaine de définition de ces fonctions est tout ou partie de l'ensemble des entiers naturels \({\mathbb N}\). Cependant, pour simplifier des calculs ou pour certaines estimations, on considèrera souvent des fonctions sur le domaine réel. On note dans toute la suite \({\mathscr F}\) l'ensemble des fonctions de \({\mathbb N}\) dans \({\mathbb R}\).

Les notations asymptotiques utilisées pour mesurer et comparer la grandeur des fonctions que nous allons voir (ou revoir) sont des extensions des notations de Landau \(o\) et \(O\) bien connues de l'étudiant dans le cadre des développements limités. C'est D. Knuth qui a largement popularisé les notations désormais classiques \(\Omega\), \(\Theta\), \(O\), pour faire le ménage dans le calcul de complexité.

Notons immédiatement que pour l'analyse de certains algorithmes, il peut être intéressant d'étudier des fonctions à plusieurs variables entières, chaque variable correspondant à la taille d'une partie des données en entrée. Par exemple l'algorithme du calcul du produit de deux entiers reçoit en entrée deux séquences de longueurs arbitraires \(n\) et \(m\) (les chiffres des deux opérandes dans une base fixée), on manipule donc des fonctions à deux variables \(f(n,m)\) et les notations asymptotiques sont similaires au cas à une variable.

Soit \(g\) une fonction de \({\mathscr F}\). On définit respectivement les notations grand omicron et grand oméga : \begin{align} O(g)&:=\{f\in{\mathscr F}\ \ |\ \ {\color{#6464FF}\exists} c>0\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq f(n)\leq cg(n)\}.\\ \Omega(g)&:=\{f\in{\mathscr F}\ \ |\ \ {\color{#6464FF}\exists} c>0\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq cg(n)\leq f(n)\}.\\ \end{align}

Que disent ces définitions ? Une fonction \(f\in O(g)\), qu'on lit \(f\) est en grand omicron de \(g,\) est majorée par une constante fois la fonction \(g\) à partir d'un certain rang \(N\). Une fonction \(f\in \Omega(g)\), qu'on lit \(f\) est en grand omega de \(g\), est minorée par une constante fois la fonction \(g\) à partir d'un certain rang \(N\). La notation grand Omicron est strictement identique à la notation grand \(O\) de Landau, on dira donc indifféremment \(f\) est en grand omicron de \(g\) ou \(f\) est en grand O de \(g\).

Une fonction peut-être à la fois majorée et minorée par des facteurs d'une fonction de référence \(g\) à partir d'un certain rang, ce que l'on résume par :

Soit \(g\) une fonction de \({\mathscr F}\). On définit la notation grand thêta : \begin{equation} \Theta(g):=\{f\in{\mathscr F}\ \ |\ \ \exists a > 0\ \;\exists b>0\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq ag(n)\leq f(n)\leq bg(n) \}. \end{equation}
Les classes de complexité sont des ensembles (infinis) de fonctions, on écrit pourtant \(f=O(g)\) au lieu de \(f\in O(g)\) en remplaçant systématiquement le symbole d'appartenance par le symbole d'égalité. Cet abus de notation est commode car il permet de définir une arithmétique sur les classes de complexité. Par exemple \(O(n)+O(n)=O(n)\) exprime que la somme de deux fonctions quelconques de l'ensemble \(O(n)\) est encore une fonction de \(O(n)\), etc.
Pour plus de clarté, si la fonction \(g\) a une expression algébrique on écrit souvent cette expression à la place de la fonction dans la notation asymptotique. Par exemple \(f=\Theta(n^2)\) si \(g:n\mapsto n^2\) ou encore \(f=O(n\log n)\) si \(g:n\mapsto n\log n\).
Soit \(f\) et \(g\) deux fonctions de \({\mathscr F}\). On a \begin{equation} \left(f=\Theta(g)\right)\ \iff\ \left(f=O(g)\ \wedge\ f=\Omega(g)\right). \end{equation}

Encore une fois, on écrit abusivement \(f=\Theta(g)\) au lieu de \(f\in \Theta(g)\) et on lit \(f\) est en grand thêta de \(g.\) Cela signifie que l'ensemble \(\Theta(g(n))\) contient toutes les fonctions que l'on peut coincer entre deux fonctions homothétiques à \(g\) à partir d'un certain rang. Autrement dit pour \(n\) suffisamment grand, les fonctions de \(\Theta(g(n))\) se comportent comme la fonction \(g\) à une constante multiplicative près.

Démontrez la proposition précédente. Démontrez que \(f=O(g)\Leftrightarrow g=\Omega(f)\).
Démontrez que la fonction définie par \(f(n):=3n^2+1\) est en \(O(n^2)\). Montrez que la fonction \(f(n):=3n^3-2n+1\) est en \(\Omega(n^3)\)
Soit \(f\) une fonction polynomiale de degré \(d\) à coefficient dominant positif. Alors \begin{equation} f=\Theta(n^d). \end{equation}
Démontrez le théorème. Utilisez la proposition 3.
Graphique gauche : \(f=\Theta(g)\). Graphique droit : \(f=\Theta(1)\)

L'expression algébrique d'une fonction et quelques connaissances sur la croissance des fonctions réelles suffisent parfois à mettre en évidence qu'une majoration est grossière, par exemple quand on affirme que la fonction \(n\mapsto 2n+1\) est en \(O(n^3)\). Ce n'est pas la définition de la notation \(O\) qui nous permet d'affirmer que cette estimation est grossière mais la connaissance de la croissance des fonctions monomiales. Ainsi l'écriture \(f=O(g)\) ne précise pas si \(f\) croit beaucoup moins vite que toute constante fois \(g\) asymptotiquement ou si \(f\) s'en approche. La notation petit \(o\) répond partiellement à cette question, quand on écrit \(f=o(g)\), on signifie que :

\[\lim_{n\rightarrow+\infty} \frac{f(n)}{g(n)}=0\]

Pour les mêmes raisons que \(f=O(g)\Leftrightarrow g=\Omega(f)\), on peut définir la notation petit omega par \(f=\omega(g)\Leftrightarrow g=o(f)\). De manière plus rigoureuse on a :

Soit \(g\) une fonction de \({\mathscr F}\). On définit respectivement les notations petit omicron et petit oméga : \begin{align} o(g)&:=\{f\in{\mathscr F}\ \ |\ \ {\color{yellow}\forall} c>0\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq f(n)\leq cg(n)\}.\\ \omega(g)&:=\{f\in{\mathscr F}\ \ |\ \ {\color{yellow}\forall} c>0\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq cg(n)\leq f(n)\}.\\ \end{align}

Sans une lecture attentive, on pourrait croire à tort qu'il s'agit des mêmes définitions que celles des notations \(O\) et \(\Omega\), mais le quantificateur universel \(\color{yellow}\forall\) remplace ici le quantificateur existentiel \(\color{#6464FF}\exists\).

Le graal est d'être en mesure de connaître le comportement asymptotique de la fonction de comp­le­xi­té et pas uniquement à une cons­tan­te multiplicative près. Si l'on définissait l'équivalence d'une fonction \(f\) à une fonction de référence \(g\) via le comportement asymptotique de leur différence \(|f(n)-g(n)|\) que l'on voudrait aussi faible que possible, \(n\mapsto n^2+n\) ne serait pas équivalente à \(n\mapsto n^2\) car leur différence \(n\mapsto n\) diverge alors que \(n\mapsto n\) devient manifestement négligeable devant \(n\mapsto n^2\) quand \(n\) est grand. Il est plus judicieux de définir l'équivalence entre \(f\) et \(g\) à l'aide de la limite : \begin{equation*} \lim_{n\rightarrow+\infty}\frac{f(n)}{g(n)} = 1. \end{equation*} qui est traduite en \((\ref{eq:equivqasympt})\) dans la définition

On dit que deux fonctions \(f\) et \(g\) de \({\mathscr F}\) sont asymp­to­ti­que­ment équi­va­len­tes, ce que l'on note \(f\sim g\) si et seulement si \begin{equation} \label{eq:equivqasympt} \forall\epsilon\in{\mathbb R}_+\ \;\exists N\in{\mathbb N}\ \;\forall n\geq N\quad \left|f(n)-g(n)\right|<\epsilon g(n). \end{equation}

Un bon moyen mnemotechnique (attention, en toute rigueur c'est faux) pour se souvenir de la si­gni­fi­ca­tion des notations asymptotiques est résumé par : \begin{align*} f=O(g)\ \ &\Leftrightarrow\ \ f\leq g \\ f=o(g)\;\,\ &\Leftrightarrow\ \ f< g\\ f=\Omega(g)\ \ &\Leftrightarrow\ \ f\geq g\\ f=\omega(g)\ \ &\Leftrightarrow\ \ f> g\\ f=\Theta(g)\ \ &\Leftrightarrow\ \ f\simeq g \\ f\sim g\ \ \ \quad &\Leftrightarrow\ \ f= g \\ \end{align*}

Pour conclure cette section, nous pouvons noter que l'emploi des notations asymptotiques permet de se débarrasser, d'une part des perturbations de la fonction de complexité pour les petites tailles des entrées avec l'introduction du rang \(N\), et d'autre part du facteur constant de l'expression de cette fonction. La contrepartie de cette souplesse apparaît surtout sur le facteur constant que l'on appelle facteur caché (ou constante cachée). Imaginons que la fonction de complexité d'un algorithme \(A\) soit \(T_A(n)=\frac{1}{8}n^2-64n+8\) et celle d'un algorithme \(B\) soit \(T_B(n)=1789n+1968\), les deux résolvant le même problème. Avec les écritures asymptotiques, on écrira \[T_A(n)=\Theta(n^2)\qquad T_B(n)=\Theta(n).\] et on privilégiera très logiquement l'algorithme \(B\) à l'algorithme \(A\) ! Pourtant l'algorithme \(B\) ne devient plus performant que l'algorithme \(A\) qu'à partir de la valeur \(n=14\,825.\) Il faut donc en conclure que l'analyse asymptotique des algorithmes est… asymptotique ! Autrement dit, pour des réalisations effectives d'algorithmes, le facteur caché peut avoir une certaine importance et pourra même valider un algorithme a priori mauvais.

Sommes et séries

Les algorithmes que nous allons étudier contiennent systématiquement des boucles (ou des appels récursifs), les calculs de complexité font donc apparaître des quantités qu'il faudra sommer, à savoir le nombre d'instructions que la machine ram doit décoder à chaque passage dans la boucle. Que ce nombre d'instructions varie ou non, ses valeurs successives constituent une suite numérique.

Soit \((u_n)_{n\in{\mathbb N}}\) une suite numérique (ici des nombres réels). On rappelle que la somme \begin{equation} S_n:=\sum_{i=0}^nu_i. \end{equation} des \(n+1\) premiers termes de la suite \((u_n)\) définit elle-même une suite \((S_n)_{n\in{\mathbb N}}\) de nombres réels qu'on appelle la série de terme général \(u_n\). Attention au vocabulaire ! En toute rigueur le terme général de la série \((S_n)_{n\in{\mathbb N}}\) devrait faire référence à \(S_n\) (qui est une somme partielle de la série \((S_n)_{n\in{\mathbb N}}\)) puisqu'il s'agit d'une suite, on fait pourtant référence au terme général \(u_n\) de la suite associée.

On dit que \((S_n)_{n\in{\mathbb N}}\) est une série convergente si c'est une suite convergente, i.e. s'il existe un nombre réel \(l\) appelé la limite de la série \((S_n)_{n\in{\mathbb N}}\), tel que \[\forall \varepsilon >0\ \ \exists N\in{\N}\ \ \forall n\in\N\ \ (n\geq N\then|S_n-l|<\varepsilon)\]

Dans le cas contraire, c'est une série divergente. Plus généralement quand une série de terme général \(u_n\) est convergente on peut noter sa limite \begin{equation} \label{serie} \sum_{i=0}^\infty u_i. \end{equation}

Une série \((S_n)_{n\in{\mathbb N}}\) de terme général \(u_n\) est dite absolument convergente si la série de terme général \(|u_n|\) est convergente. Les deux écritures \begin{equation} \sum_{i=0}^\infty u_i,\quad\text{et}\quad \sum_{i\in{\mathbb N}}u_i \end{equation} ne sont pas équivalentes. La première indique explicitement l'ordre dans lequel on rajoute les termes de la suite dans la somme partielle, et ceci a une importance capitale pour la convergence ou la divergence de la série. L'ordre n'est pas spécifié dans la seconde ce qui laisse entendre qu'il ne change rien à la limite ce qui est faux. Considérons par exemple la suite de terme général \begin{equation} \label{eq:defseq} u_i=\begin{cases} 0,&\text{si \(i\) est pair}.\\ 1,&\text{si \(i\) est impair}. \end{cases} \end{equation}

autrement dit, il s'agit de la suite alternée \(010101\ldots\) Dans ce cas précis, il est évident que si l'on décompose la somme sur les indices pairs et impairs, en commençant la sommation sur les indices pairs, on converge vers \(0\), alors que la série diverge. Par contre, pour une série absolument con­ver­gen­te, il y a égalité et l'ordre de la sommation n'a pas d'incidence sur le résultat, on réservera donc la seconde écriture aux séries absolument convergentes.

Comme nous venons de le constater pour la suite définie en \((\ref{eq:defseq})\), une suite peut être divergente sans pour autant tendre vers l'infini (positivement ou négativement). On rappelle qu'une suite \((u_n)\) diverge vers \(+\infty\) si et seulement si elle satisfait l'as­ser­tion suivante : \begin{equation} \forall A\in{\mathbb R}^+\ \ \exists N\in{\mathbb N}\ \ \forall n\geq N\ \quad (n\geq N\Rightarrow u_n > A) \end{equation} Par exemple, la série de Grandi de terme général \(u_n=(-1)^n\) est divergente, ses sommes par­tiel­les sont alternativement les deux valeurs \(0\) et \(1\), elle ne diverge manifestement pas vers l'infini.

La propriété de linéarité pour des sommes finies \begin{equation} \sum_{i=1}^n(\lambda u_i+b_i)=\lambda\sum_{i=1}^nu_i+\sum_{i=1}^nb_i \end{equation} est conservée pour des séries convergentes.

[Critère de d'Alembert] Soit \((u_n)_{n\in{\mathbb N}}\) une série à termes positifs non-nuls à partir d'un certain rang. S'il existe un réel \(l\) tel que \begin{equation} \lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_n}=l. \end{equation} Alors la série \((u_n)\) converge si \(l<1\), diverge si \(l>1\). Si \(l=1\) on ne peut pas conclure.
Considérons la série de terme général \(u_n:=2^{-n}\). On a \(u_{n+1}/u_n=\frac{1}{2}\) et le critère de d'Alembert nous permet d'affirmer que la série est convergente (sans pour autant fournir la somme de la série qui ici vaut 2). Pour \(n\) entier positif, le \(n\)-ème nombre harmonique est la somme partielle notée \(H_n\) de la série de terme général \(\frac{1}{n}\) : \begin{equation*} H_n:=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n}. \end{equation*} Ici le critère de d'Alembert ne nous apprend pas grand chose sur la convergence de cette série puisque \(\lim_{n\rightarrow+\infty}\frac{n}{n+1}=1\), en fait il s'agit d'une série divergente (cf. exercice).

S'il est simple de calculer la somme d'une série arithmétique ou géométrique, il peut être très délicat d'obtenir directement via des formules algébriques l'expression de la somme d'une série arbitraire. On peut parfois deviner l'expression de cette somme sans pour autant être capable de l'obtenir directement. Dans ce cas, on utilise souvent un raisonnement par récurrence pour valider (ou non) l'expression supposée.

On veut montrer que pour tout nombre réel \(b>1\) il existe une constante \(c>0\) (qui dépend donc a priori de \(b\)) telle que \begin{equation} \label{eqcb} {\color{#FF0}\sum_{i=0}^nb^i}\leq cb^n. \end{equation} On ne connaît pas encore la constante, mais le raisonnement par récurrence va nous permettre de la déterminer. On se donne un entier positif \(b\) et on considère le prédicat \(P(n)\) que constitue l'inégalité \((\ref{eqcb})\). Dans une preuve par récurrence, on commence traditionnellement par l'initialisation, mais ici la preuve de l'hérédité va nous fournir des indications sur la constante \(c\) à considérer. On procède comme si l'on connaissait déjà cette constante \(c\) et on calcule la somme au rang \(n+1\) : \begin{equation} \sum_{i=0}^{n+1}b^i=\left({\color{#FF0}\sum_{i=0}^nb^i}\right)+b^{n+1}. \end{equation} L'hypothèse de récurrence nous permet d'appliquer l'inégalité \((\ref{eqcb})\) : \begin{align} \sum_{i=0}^{n+1}b^i&\leq cb^n+b^{n+1}\\ &=\left(\frac{1}{b}+\frac{1}{c}\right)cb^{n+1}\\ &\leq cb^{n+1}\\ \end{align} la dernière inégalité n'est vraie que si \((1/b+1/c)\leq 1\), soit dès que \(c\geq b/(b-1)\). Il suffit à présent de montrer l'initialisation pour la constante \(c:=b/(b-1)\) (par exemple). Pour \(n=0\) on a \begin{equation} \sum_{i=0}^0b^i=1 < \frac{b}{(b-1)} \end{equation} Notons que comme \(b > 1\), on a \(b/(b-1) < 2\), ce qui prouve au passage qu'il existe une constante indépendante de \(b\) qui satisfait l'inégalité \((\ref{eqcb})\), par exemple \(c=2\). C'est un exemple didactique, dans ce cas particulier il est parfaitement inutile d'avoir recours à une récurrence puisqu'on est en présence d'une suite géométrique de raison \(b\) : \begin{align*} {\color{#FF0}\sum_{i=0}^nb^i}&=\frac{b^{n+1}-1}{b-1}\\ &\leq \frac{b^{n+1}}{b-1}=\left(\frac{b}{b-1}\right)b^n. \end{align*}

Une autre méthode très utile pour approximer une somme consiste à la majorer et/ou minorer par l'in­té­gra­le d'une fonction monotone. On est en effet souvent en mesure d'exprimer le nombre d'ins­truc­tions à décoder dans une boucle à l'aide d'une fonction qui dépend d'un indice de boucle. En al­go­ri­thmi­que cette fonction est quasi systématiquement monotone, ce qui explique la popularité de ce pro­cé­dé de calcul.

Soit \(f\) une fonction réelle positive et \(m\) et \(n\) deux entiers naturels tels que \(m < n\). Si \(f\) est monotone et croissante, alors \begin{equation} \label{majint} \int_{m-1}^nf(x)dx \leq {\color{#F0F}\sum_{i=m}^nf(i)} \leq \int_{m}^{n+1}f(x)dx. \end{equation} Si \(f\) est monotone et décroissante, alors \begin{equation} \int_{m}^{n+1}f(x)dx\leq\sum_{i=m}^nf(i)\leq\int_{m-1}^{n}f(x)dx. \end{equation}
Nous ne démontrons le résultat que pour une fonction monotone croissante, la preuve est similaire pour une fonction décroissante. Dans la figure ci-dessous, les \(n-m+1\) rec­tang­les ont tous une base de longueur \(1\) et ont pour hauteurs \(f(i)\) pour \(i\in[m,n]\). La somme de leurs aires est égale à la la somme de l'encadrement \((\ref{majint})\). Comme ils sont situés sous la courbe représentative de la fonction \(f\), l'aire de la courbe entre les abscisses \(m\) et \(n+1\) fournit une majoration.
Majoration et minoration d'une série.

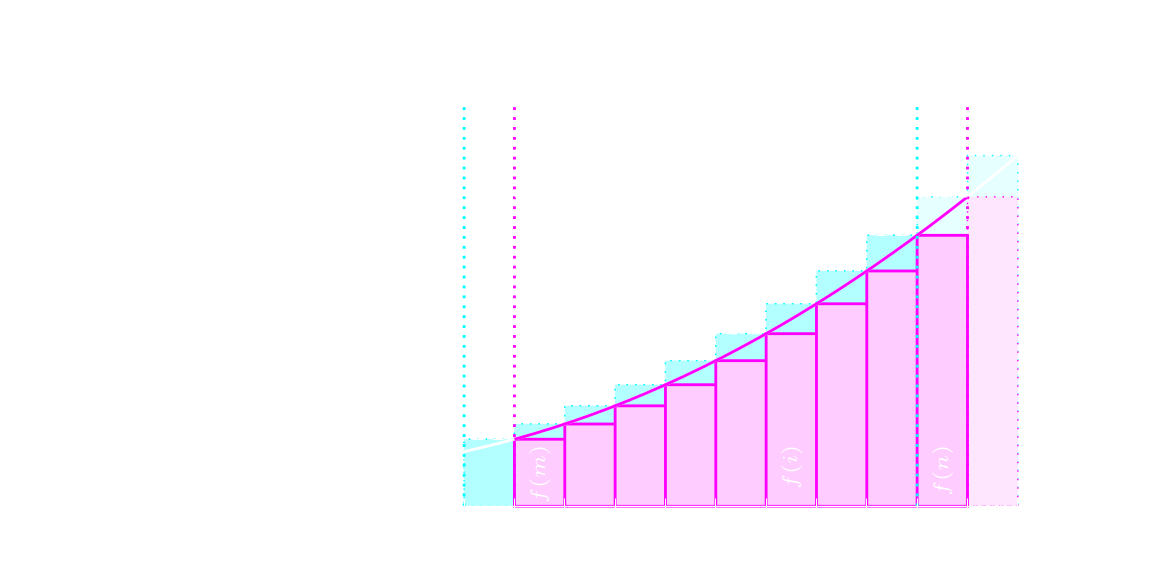
Si on décale tous ces rectangles d'une unité vers la gauche, ils passent alors au-dessus de la courbe et cette fois l'aire de la courbe entre les abscisses \(m-1\) et \(n\) minore la somme.

Inversement, pour estimer la surface de l'aire délimitée par la courbe et l'axe des abscisses entre \(m\) et \(n\), on diminue indéfiniment la largeur du rectangle et c'est de cette manière que l'on introduit l'intégrale d'une fonction au sens de Riemann.
Démontrez que la somme de la série de terme général \(2^{-n}\) est égale à 2. Démontrez que la série harmonique n'est pas convergente à l'aide du théorème ci-dessus. Puis en remarquant que \begin{equation*} 1+\frac{1}{2}+\underbrace{\frac{1}{3}+\frac{1}{4}}_{> \frac{1}{4}+\frac{1}{4}}+\underbrace{\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}}_{> \frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}}+ \underbrace{\frac{1}{9}+\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+\frac{1}{16}}_{> \frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}}+\dots \end{equation*} démontrez d'une autre façon que cette série est divergente.

Ordres de grandeur

Comme nous l'avons vu, c'est le comportement asymptotique des fonctions de complexité qui nous intéresse et il est bon de connaître les comportements les plus communs possibles ainsi que le vocabulaire associé. On se donne \(T(n)\) une fonction de complexité où \(n\) désigne la taille de la donnée à traiter. On résume ces comportements ci-dessous avec \(p(n)\) qui désigne une fonction polynomiale (à coefficient dominant positif). Les fonctions sont rangées dans l'ordre (strictement) croissant de leurs complexités :

Notons qu'un algorithme est dit de complexité polynomiale si sa fonction de complexité est majorée par une fonction polynomiale. Ainsi un algorithme de complexité \(O(n\log n)\) est dit de complexité polynomiale car \(\forall n\in{\mathbb N},\ n\log n \leq n^2\), quand bien même la fonction \(n\mapsto n\log n\) n'est pas stricto sensu une fonction polynomiale.

Calculs avec les notations asymptotiques

Nous emploierons très souvent les notations asymptotiques dans des calculs comme s'il s'agissait de fonctions. Il est nécessaire de comprendre l'intérêt de cet abus de langage et des pièges qui en découlent. Par exemple, que signifie l'égalité \(O(n^2)+O(n)=O(n^2)\) ? Il faut remplacer dans le calcul chaque notation asymptotique par une fonction quelconque de sa classe. Ici formellement on se donne deux fonctions \(f_1\) et \(f_2\) telles que : \begin{align*} &\exists c_1\in{\mathbb R}_+^*\ \;\exists N_1\in{\mathbb N}\ \;\forall n\geq N_1\quad 0\leq f_1(n)\leq c_1n^2;\\ &\exists c_2\in{\mathbb R}_+^*\ \;\exists N_2\in{\mathbb N}\ \;\forall n\geq N_2\quad 0\leq f_2(n)\leq c_2n. \end{align*} En notant \({\color{yellow}N}:=\max\{N_1,N_2\}\), on en déduit que \begin{align*} \forall n\geq N\quad 0\leq f_1(n)+f_2(n) &\leq c_1n^2+c_2n\\ &\leq c_1n^2+c_2n^2\\ &= (c_1+c_2)n^2 \end{align*}

Autrement dit, si on définit \({\color{yellow}c}:=c_1+c_2\), on vient de prouver que \[\exists {\color{yellow}c}\in{\mathbb R}_+^*\ \;\exists {\color{yellow}N}\in{\mathbb N}\ \;\forall n\geq N\quad 0\leq f_1(n)+f_2(n)\leq cn^2, \] c'est-à-dire \(f_1+f_2=O(n^2)\) ce qui justifie l'écriture \(O(n^2)+O(n)=O(n^2)\). L'exercice suivant montre qu'il faut prendre garde au sens des expressions.
Montrez que si \(k\in{\mathbb R}\) est une constante strictement positive, alors \[k\times O(g(n))=O(g(n))\] mais qu'en revanche \[n\times O(g(n))=O(ng(n)).\] Calculez \(\Theta(n)-\Theta(n)\).

Cas de la notation \(\Theta(1)\)

La notation \(\Theta(1)\) est particulièrement utile à plus d'un titre. Elle sert intensivement pour le calcul de la complexité d'un algorithme quand celui-ci est décrit dans un langage informel comme celui que nous utilisons. Le calcul de la complexité pour la machine RAM se fait en comptant le nombre d'instructions décodées, en revanche dans notre pseudo-langage algorithmique la notion d'instruction n'est pas précisément définie et nous savons qu'une expression du type \(x\leftarrow 3.12 x-6\) a un coût (en nombre de cycles machine sur un modèle bien réel) bien plus important qu'un incrément \(x \leftarrow x +1\) par exemple. Le coût qui était unitaire dans notre modèle ne l'est plus avec notre pseudo langage.

L'introduction de la notation \(\Theta(1)\) permet de nous affranchir de ce problème si l'on est attentif. En effet, une instruction élementaire dans notre pseudo-langage pourrait être traduite en un groupe d'instructions équivalent pour la machine RAM. Une opération d'incrémentation comme \(x \leftarrow x+1\) est directement traduite par l'instruction 

INC x
en supposant que \(x\) désigne le registre mémoire associé à la variable \(x\), et avec les mêmes conventions, une instruction comme \(x \leftarrow x+y\) serait traduite par les trois instructions 
LOAD x
ADD y
STORE x
De la même manière, une instruction conditionnelle comme SI \(x+2 < y\) ALORS s'écrirait 
LOAD x
ADD #2
SUB y
JUML adresse
Dans les trois cas, le nombre d'instructions est borné inférieurement et supérieurement par deux constantes, ici \(1\) et \(4\). On peut donc dire ici qu'une instruction a un coût de \(\Theta(1)\) et on ne se préoccupe plus de l'inflation engendrée par la traduction. Bien entendu la diversité des instructions possibles en pseudo-langage algorithmique et l'absence de grammaire formelle nous empêche d'étudier cette inflation de manière exhaustive, mais nous serons en mesure de déterminer aisément si elles ont un coût en \(\Theta(1)\) ou non.