La récursivité

Base récurrente, autodéfinition

La suite de Fibonacci

Au début du xiii-ème siècle, le mathématicien italien Léonard de Pise surnommé Fibonacci, a proposé de décrire l'évolution d'une population de lapins (dont tout le monde sait qu'ils se reproduisent comme des…). L'hypothèse simplificatrice est que chaque mois deux lapins adultes mâle et femelle donnent naissance à 2 lapereaux mâle et femelle et qu'il faut un mois à un lapereau pour devenir adulte et pouvoir procréer. La question est de savoir combien de couples de lapins (ou lapereaux) il y aura dans le clapier après \(n\) mois ? On suppose que le clapier contient initialement 2 lapereaux.

À l'étape 0, il y a donc un seul couple de lapereaux. Après un mois, ces lapins sont adultes. Après deux mois ce couple de lapins donne naissance à leur premier couple de lapereaux, il y a donc 2 couples, etc.

Dessinez un arbre de profondeur 5 pour représenter la croissance de la population des lapins après 5 mois, chaque nœud contenant un couple de lapins ou lapereaux. Démontrez ensuite que le nombre de couples de lapins dans le clapier après \(n\) mois est égal à la somme du nombre de couples de lapins des deux mois précédents.

En mathématiques, la suite de Fibonacci \((F_n)_{n\in{\N}}\) est une suite d'entiers naturels dont le terme courant est égal à la somme des deux termes précédents, les deux premiers termes de la suite étant \(F_0=0\) et \(F_1=1\). On peut exprimer cette définition à l'aide de la récurrence :

\begin{equation}\label{eq:fibo} {\color{#DDA}F_n}= \begin{cases} 1&\text{si}\ n\in\{0,1\},\\ F_{n-1}+F_{n-2}&\text{sinon.} \end{cases} \end{equation}
Les \(n:=\) premiers termes de cette suite sont :
La définition récurrente (\ref{eq:fibo}) ne permet pas de calculer la valeur \(F_n\) directement, c'est-à-dire en effec­tuant un nombre d'opérations indépendants de l'entier \(n\). Nous verrons en exercice comment obtenir une formule directe. Mais pour le moment, il faut calculer tous les termes qui précèdent. On déduit facilement un algorithme itératif pour calculer le \(n\)-ème terme \(F_n\), il suffit de conserver en mémoire à chaque étape les deux termes précédents, les additionner (instruction #16) puis les mettre à jour (instructions 17 et 18 en faisant attention à l'ordre des copies), pour la prochaine étape : 
ALGORITHME Fibonacci(n):entier
DONNEES
   n: entier
VARIABLES
   F,x,y,i: entiers
DEBUT
   SI n < 2 ALORS
      RENVOYER 1
   SINON
      x ← 1
      y ← 1
      i ← 2
      TQ i ≤ n FAIRE
         F ← x + y
         x ← y
         y ← F
      FTQ    
      RENVOYER F
   FSI 
FIN

Récurrence et récursivité

De la même manière que l'on peut définir une suite ou une fonction récurrente en mathématiques, on peut définir un algorithme récursif en informatique. Le parallèle est parfaitement adapté puisqu'une fonction récursive s'adapte en général immédiatement en son équivalent algorithmique récursif.

On appelle algorithme récursif tout algorithme qui fait appel à lui-même.

L'algorithme précédent s'écrit récursivement : 

ALGORITHME Fibonacci(n):entier
DONNEES
   n: entier
DEBUT
   SI n < 2 ALORS
      RENVOYER 1
   SINON
      RENVOYER Fibonacci(n-1) + Fibonacci(n-2)
   FSI 
FIN

L'algorithme est uniquement constitué par les deux blocs de l'instruction conditionnelle SI / ALORS / SINON. Le premier bloc (instruction #6) constitue ce que l'on appelle la base récurrente qui correspond à la situation que l'algorithme sait traiter sans faire appel à lui-même. C'est l'homoloque informatique de l'initialisation dans un raisonnement par récurrence en mathématiques. La seconde appelée autodéfinition concerne la partie de l'algorithme qui fait référence à lui même, ici un unique appel récursif (instruction #8). C'est l'homoloque informatique de l'hérédité dans un raisonnement par récurrence en mathématiques.

L'idée sous-jacente, tout comme pour une récurrence, est que le ou les appels récursifs se font sur des instances plus petites du ou des paramètres de l'algorithme, ici \(n-1\) et \(n-2\) au lieu de \(n\). Comme l'algorithme sait traiter le cas de base, la suite des appels récursifs sur des instances de plus en plus petites aboutira inexorablement à un appel sur la ou les instances de la base récurrente ce qui achèvera le processus. Retenons donc les deux concepts clefs d'un algorithme récursif : la base récurrente et l'autodéfinition.

La plupart des langages de programmation modernes autorisent les définitions récursives des fonctions et même la récursivité croisée, où une fonction \(A\) fait appel à une fonction \(B\) qui appelle \(A\). Cette liberté d'écriture offerte au programmeur repose sur l'existence d'une pile. À chaque appel de la fonction, un bloc d'activation contenant les paramètres d'appel de la fonction, ses variables locales et sa valeur de retour est empilé. La fonction travaille toujours avec les variables du bloc d'activation au sommet de la pile. Si elle est appelée à nouveau récursivement, un nouveau bloc d'activation est empilé et la fonction travaillera avec les variables de ce nouveau bloc et ainsi de suite jusqu'à ce que sa valeur de retour soit instanciée et qu'elle termine son exécution, moment où le bloc d'activation est dépilé.

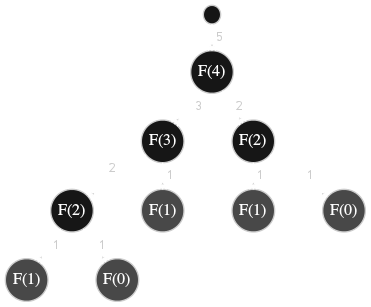
Ainsi, pour l'algorithme récursif Fibonacci, l'algorithme opère sur une nouvelle variable \(n\) et une nouvelle valeur de retour placées au sommet d'une pile à chaque nouvel appel. La figure ci-dessous contient l'arbre des appels récursifs de l'algorithme Fibonacci pour la valeur \(n=4\). La valeur de retour de l'algorithme est l'étiquette des branches.

Arbre des appels de l'algorithme Fibonacci pour \(n=4\). Les étiquettes des arcs sont les valeurs de retour. Les feuilles en gris correspondent à la base récurrente.

La table suivante décrit l'état de la pile au fur et à mesure des appels récursif de l'algorithme Fibonacci pour les valeurs \(n\) inférieures ou égales à 5 (afin de limiter la taille de l'affichage). Dans la pile, le bloc d'activation contient la valeur \(n\) et la valeur de retour ret de l'algorithme (matérialisée par un point tant qu'elle n'a pas été instanciée).

Saisissez la valeur \(n:=\).

Trace de la pile lors de l'exécution de l'algo­ri­thme Fibonacci pour \(n=\).
La possibilité d'écrire des algorithmes récursifs donne une souplesse considérable et parfois décisive. Il peut être très délicat d'écrire une méthode itérative pour résoudre un problème car sa nature est récursive.

Mais, ce qui distingue fondamentalement une méthode récursive d'une méthode itérative, c'est la nécessité ou non de conserver tous les calculs intermédiaires, autrement dit la nécessité de disposer d'une pile ou non. On utilise donc une pile si l'on a affaire mathématiquement à une récurrence forte ou une récurrence faible. Dans le premier cas, on a besoin de tous les \(P(k)\) pour \(k\leqslant n\) pour obtenir \(P(n+1)\), dans le second on n'a besoin que de l'étape précédente \(P(n)\).

Ainsi le calcul du \(n\)-ème terme de la suite de Fibonacci n'est pas un problème de nature récursive. En effet, seuls deux termes nécessitent d'être conservés à chaque étape pour pouvoir calculer le prochain, il est donc artificiel et dispandieux de conserver toutes les valeurs \(F_i\) pour \(i\lt n\). L'algorithme itératif Fibonacci initialement proposé est à privilégier.

Il est également important de noter que dans la version récursive, outre l'empilement superflu d'une quantité non négligeable d'informations, certains calculs sont effectués plusieurs fois inutilement comme le montre l'arbre des appels récursifs dans la figure 1 avec les deux nœuds \(F(2)\) qui par construction sont la racine du même sous-arbre. C'est un écueil majeur et très commun lorsqu'on écrit des algorithmes récursifs.

Évaluez la complexité en temps et en mémoire des deux algorithmes qui calculent le \(n\)-ème terme \(F_n\) de la suite de Fibonacci et comparez.
On rappelle la définition de la fonction factorielle \({\N}\rightarrow{\N}\) définie par \[n!=n(n-1)(n-2)\ldots 2\times 1\] Écrivez un algorithme récursif pour calculer cette fonction. Tracez la pile d'exécution pour \(n=4\). La fonction factorielle est-elle une fonction de nature récursive ? Écrivez un algorithme itératif pour calculer cette fonction. Évaluez la complexité en temps et en mémoire des deux algorithmes et comparez.
Soient \(p\) et \(n\) deux entiers tels que \(0\leq p\leq n\). La formule du triangle de Pascal : \begin{equation} \binom{n}{p}= \begin{cases} 1&\text{si}\ p=0\ \text{ou}\ p=n,\\ \binom{n-1}{p}+\binom{n-1}{p-1}&\text{sinon}. \end{cases} \end{equation} fournit une définition récursive du coefficient binomial \(\binom{n}{p}\). Écrivez un algorithme récursif Binomial pour le calculer. Tracez la pile d'exécution pour \(n=3\) et \(p=2\). La fonction binomiale est-elle une fonction de nature récursive ? Écrivez un algorithme itératif pour calculer cette fonction. Évaluez la complexité en temps et en mémoire des deux algorithmes et comparez.
(Formule de Binet). La suite de Fibonacci est une suite récurrente linéaire d'ordre 2, c'est-à-dire une suite à valeurs dans un corps commutatif, ici \({\mathbf R}\), telle que le terme courant est une combinaison linéaire des deux termes précédents. En notant \(U_n\) le vecteur \((F_n,F_{n+1})\) de \({\mathbf R}^2\), calculez la matrice \(2\times 2\) notée \(A\) telle que \(U_{n+1}=AU_n\). En déduire que \(U_{n-1}=A^{n-1}U_0\). Diagonalisez la matrice \(A\) et en déduire une formule pour calculer directement \(F_n\).

Les tours de Hanoï.

Si ni le calcul de la suite de Fibonacci, ni le calcul de la factorielle d'un entier ne sont des problèmes de nature récursive, malgré ce que suggèrent leurs définitions récurrentes, quel type de problème jus­ti­fie une écriture récursive ?

Présentation du problème.

Nous allons aborder un problème très classique en informatique qui a le mérite d'illustrer la puissance de l'écriture récursive en fournissant une solution simple et particulièrement élégante. La résolution de ce problème demanderait des efforts beaucoup plus conséquents s'il fallait se limiter à une écriture itérative classique pour calquer la méthode manuelle. Sans une analyse plus approfondie, il faudrait ni plus ni moins recréer une pile calquant ce que fait la pile d'exécution dans la version récursive.

Nous verrons en exercice plus loin qu'il est malgré tout possible de se passer d'une pile avec une solution itérative. Cela n'a rien d'étonnant, le mécanisme de résolution de ce casse-tête se trouve assez facilement après quelques tâtonnements et il est manifeste qu'un joueur n'a pas besoin de conserver en mémoire l'intégralité des manipulations effectuées pour déterminer quel est le mouvement suivant, ce jeu ne s'adresse pas à des mutants.
Le problème des tours de Hanoï avec \(n=8\) disques.

Le problème des tours de Hanoï, imaginé par l'arithméticien français Edouard Lucas à la fin du xix-ème siècle, consiste à déplacer les disques d'une pile de \(n\) disques de diamètres décroissants de leur tour d'origine vers une autre tour en s'aidant d'une troisième tour auxiliaire. Il faut respecter les deux conditions suivantes :

  1. On ne peut empiler qu'un seul disque à la fois ;
  2. On ne peut empiler un disque que sur un disque de diamètre supérieur (ou sur une tour vide).
Ce jeu est devenu un casse-tête populaire qui se vend dans la plupart des boutiques de jeux. La photo ci-dessus est celle de mon exemplaire personnel qui contient 8 disques.

Dans la suite les tours seront numérotées de 1 à 3 de la gauche vers la droite et nous coderons \(x\rightarrow y\) le déplacement du disque au sommet de la pile de la tour \(x\) vers le sommet de la pile de la tour \(y\). Bien entendu ce déplacement est supposé respecter la règle 2. Par convention la pile est initialement placée sur la première tour et il faut la déplacer vers la troisième tour.

Le problème est trivial pour \(n=1\), une solution évidente est \(1\rightarrow 3\). Pour \(n=2\) c'est à peine plus compliqué, la suite des déplacements \(1\rightarrow 2,\ 1\rightarrow 3,\ 2\rightarrow 3\) constitue une solution. Pour \(n=3\) cela demande un peu plus de réflexion : \[1\rightarrow 3,\ 1\rightarrow 2,\ 3\rightarrow 2,\ 1\rightarrow 3,\ 2\rightarrow 1,\ 2\rightarrow 3,\ 1\rightarrow 3.\] Notons déjà qu'il existe plusieurs solutions pour une instance de taille \(n\) et qu'il est naturel de s'interroger sur l'optimalité des solutions en termes de nombre de déplacements à réaliser. Il est aisé de prouver que les solutions fournies pour \(n=1\) et \(n=2\) ci-dessus sont optimales. Nous étudierons cette question dans l'étude de la complexité de l'algorithme qui résout ce problème.

Algorithme de résolution du problème.

Analysons le problème. Notons \(A\), \(B\) et \(C\) les trois tours. Pour déplacer \(n\) disques de la tour \(A\) à la tour \(C\), il faut déplacer \(n-1\) disques de la tour \(A\) à la tour \(B\) puis déplacer le dernier disque de la tour \(A\) à la tour \(C\) et finalement déplacer les \(n-1\) disques de la tour \(B\) à la tour \(C\). Autrement dit si l'opération Déplacer(n,A,C) signifie déplacer \(n\) disques de la tour \(A\) vers la tour \(C\), alors elle peut se décomposer en trois opérations plus simples :

  1. Déplacer(n-1,A,B) ;
  2. Déplacer(1,A,C) ;
  3. Déplacer(n-1,B,C).
On vient de décrire la partie autodéfinition de l'algorithme récursif Déplacer. Mais pour que l'algorithme soit complet, il faut que les appels récursifs s'arrêtent, il faut alors déterminer les valeurs des paramètres pour lesquels on sait comment traiter le problème directement sans s'appuyer sur la récursion. La base récurrente est ici très simple, s'il ne reste qu'un disque, il suffit de le déplacer de sa tour d'origine vers la tour d'arrivée. L'algorithme complet s'écrit donc : 
ALGORITHME Déplacer(n,X,Y)
DONNEES 
   n,X,L: entiers
DEBUT
   SI (n = 1)
      Afficher(X, "→", Y)
   SINON
      Déplacer(n-1, X, 6-X-Y)
      Afficher(X, "→", Y)
      Déplacer(n-1, 6-X-Y, Y)
   FSI
FIN

Les paramètres \(X\) et \(Y\) de l'algorithme désignent respectivement la tour d'origine et la tour de destination des \(n\) disques.

Démontrez que si les tours sont numérotées de 1 à 3 et que si \(X\) et \(Y\) désignent le numéro de deux tours distinctes alors la troisième tour a nécessairement pour numéro \(6-X-Y\).

L'animation suivante montre l'état des trois tours lors de la résolution du problème des tours de Hanoï par l'algorithme Déplacer pour un nombre de disque \(n\) tel que \(1\leq n\leq 16\).

Saisissez le nombre de disques \(n:=\).

Solution optimale au problème des tours de Hanoï pour \(n=\)
Programmez l'algorithme Déplacer et comptez empiriquement le nombre d'appels récursifs réalisés. Tracez la courbe du nombre d'appels en fonction du nombre de disques \(n\) avec Gnuplot.

Complexité de l'algorithme et optimalité.

Calculons la complexité de cet algorithme. Le coût de la base récurrente est constant en \(\Theta(1)\) et le traitement réalisé dans le corps de l'algorithme, hormis les appels récursifs, a un coût constant \(\Theta(1)\). Il y a exactement deux appels récursifs. La fonction de complexité \(T\) est donc donnée par l'équation suivante : \begin{equation}\label{eqhan} T(n)=\begin{cases} \Theta(1)&\text{si}\ n =1,\\ 2T(n-1)+\Theta(1)&\text{sinon}. \end{cases} \end{equation} En substituant successivement les \(T(k)\) par leurs valeurs dans l'expression (\ref{eqhan}), on arrive à \begin{align*} T(n)&=2^nT(1)+\Theta(1)\sum_{i=0}^{n-1}2^i\\ &=2^n\Theta(1)+\Theta(1)(2^n-1)\\ &=\Theta(2^n). \end{align*}

En vous inspirant du calcul de la fonction de complexité de l'algorithme Déplacer, montrez que le nombre de mouvements de disques effectués si la pile initiale contient \(n\) disques est exactement \(2^n-1.\)
Pour déplacer \(n\) disques, l'algorithme Déplacer réalise \(2^n-1\) mouvements. C'est le nombre minimal de mouvements et c'est l'unique façon d'obtenir ce minimum.
La première partie de l'énoncé a été traitée dans l'exercice précédent. On montre la deuxième partie par récurrence sur le prédicat \(P(n)\) suivant :
L'algorithme Déplacer réalise la suite optimale de mouvements pour déplacer \(n\) disques d'une tour à une autre.
C'est évident pour \(n=1\). On numérote les \(n+1\) disques sur la première tour de \(1\) à \(n+1\) dans l'ordre croissant de leurs diamètres. Pour les déplacer vers la troisième tour, compte tenu des règles imposées, il faut nécessairement qu'à une certaine étape le disque \(n+1\) en bas de la pile soit déplacé de la tour 1 vers la tour 3. Ceci n'est possible que si la pile des \(n\) disques au-dessus est placée sur la tour 2. Ainsi pour déplacer optimalement les \(n+1\) disques de la tour \(1\) vers la tour \(3\), il faut déplacer optimalement la pile des \(n\) disques au sommet de la tour \(1\) vers la tour \(2\) au préalable pour pouvoir déplacer le disque \(n+1\) de la tour 1 vers la tour 3 et enfin déplacer optimalement la pile des \(n\) disques de la tour \(2\) vers la tour \(3\). L'hypothèse de récurrence permet de conclure.
Calculez la complexité en espace de l'algorithme Déplacer.
On numérote les trois tours 0, 1 et 2 de la gauche vers la droite. Soit \(n\) le nombre de disques sur la tour #0. On considère les deux opérations suivantes :
  1. Déplacer le plus petit disque de sa tour \(x\) vers la tour \(x+1\pmod 3\) si \(n\) est pair, vers la tour \(x-1\pmod 3\) si \(n\) est impair ;
  2. Déplacer un autre disque (un seul des deux autres disques peut en effet être déplacé).
Pour les 4 instances \(n=1, 2, 3\) et \(4\), répétez ces deux règles jusqu'à ce que la tour #0 soit vide. Que constatez-vous ? Écrivez un algorithme itératif Décaler qui répète ces déplacements jusqu'à ce que la tour #0 soit vide (en fonction de \(n\)). Démontrez par récurrence que cette méthode est optimale. Calculez la complexité en temps et en espace de cet algorithme ? Comparez ces complexités avec celles de l'algorithme récursif Déplacer. Quel est l'algorithme le plus efficace ?

On rappelle que le poids de Hamming \(w(k)\) d'un entier \(k\) est le nombre de chiffres non-nuls dans son écriture binaire. Ainsi \(w(13)=3\) car \(13=1101_2\). Écrivez un algorithme récursif Poids qui calcule le poids d'un entier \(k\) passé en paramètre en montrant préalablement que \begin{equation} w(k)=\begin{cases} w(t),&\text{si}\ k=2t\\ w(t)+1,&\text{si}\ k=2t+1.\\ \end{cases} \end{equation} Calculez la complexité de cet algorithme en ne tenant compte que du nombre de tests réalisés. À l'aide de l'algorithme Poids écrivez un algorithme Peser qui construit une table de \(W\) telle que \(W[i]=w(i)\). Quelle est la complexité de cet algorithme ? Montrez que l'on peut écrire un algorithme qui réalise la même opération en \(\Theta(n)\) avec un facteur caché de \(\frac{1}{2}\).
Écrivez un algorithme récursif pour calculer le \(n\)-ème terme de la suite de Syracuse. Comparez le avec l'algorithme itératif.
On appelle dérécursivation tout procédé qui consiste à transformer un algorithme récursif en un algorithme équivalent mais qui ne contient aucun appel récursif (algorithme que l'on qualifie communément d'itératif). On dit qu'un algorithme est récursif terminal s'il ne contient qu'un appel récursif et qu'il s'agit de la dernière instruction.

Expliquez comment dérécursiver un algorithme récursif terminal avec une boucle. Plus généralement expliquez comment dérécursiver un algorithme récursif quelconque à l'aide d'une pile auxiliaire globale.

Les chapitres suivants consacrés à la résolution de trois problèmes classiques, le problème des reines, le problème du cavalier et le problème du le problème du Sudoku sont des exemples où la connaissance de l'historique est un élément clef pour élaborer une stratégie.

Complexité des algorithmes du type diviser pour régner

Diviser pour régner

Principe algorithmique

Le principe algorithmique dit diviser pour régner consiste à :

  1. Diviser l'instance d'un problème en sous-instances,
  2. Traiter indépendamment ces sous-instances,
  3. Combiner les différents résultats obtenus pour construire une solution au problème initial.

Les algorithmes qui s'appuient sur ce principe sont souvent récursifs et opèrent sur des instances de plus en plus petites jusqu'à ce que la taille de l'instance à traiter rende la résolution du problème simple voire triviale. La recherche dichotomique fait partie des premiers algorithmes étudiés de ce type. Notons que l'algorithme d'addition étudié en classe primaire peut également être classé dans cette catégorie bien qu'il soit itératif. Les nombres sont segmentés en chiffres sur lesquels l'opération d'addition est élémentaire puisqu'elle consiste à effectuer une simple recherche en table, la pro­pa­ga­tion de la retenue éventuelle combine les additions des sous-instances pour obtenir le ré­sul­tat.

Ce principe algorithmique s'est avéré très efficace pour obtenir de meilleures fonctions de complexité qu'avec une approche globale, d'où sa popularité. Nous le retrouverons dans d'autres algorithmes fondamentaux dans les prochains chapitres comme l'algorithme du TriFusion et du TriRapide mais également dans l'algorithme de recherche par Dichotomie ou encore la multiplication rapide avec l'algorithme de Ka­rat­su­ba ou la transformée de Fourier discrète.

Calcul de la complexité

La suite des instructions qui définissent un algorithme récursif sont constituées d'un certain nombre d'appels récursifs, que l'on notera \(a\), sur des entrées \(y_i\) dont la taille est une fraction de la taille \(n:=\#x\) de l'entrée initiale \(x\), disons \(n/b\). Les opérations réalisées par l'algorithme en dehors de ces \(a\) appels récursifs, pré-traitement (incluant le partitionnement de \(x\)) et post-traitement, a un coût noté \(f(n)\). La structure d'un algorithme récursif est synthétisée de la manière suivante : 

ALGORITHME Générique-Récursif(x,n)
DONNEES
   x: paramètre
   n: entier // taille de x
VARIABLES
   i: entier
   y: liste
DEBUT
   SI (n > constante) ALORS
      Pré-traitement
      i ← 1
      TQ i ≤ a FAIRE
         Générique-Récursif(yi,n/b)
         i ← i + 1
      FTQ
      Post-traitement
   FSI
FIN

Pour résumer, on a les variables suivantes :

Dans le cas où \(n=1\), le coût de traitement est supposé constant, donc en \(\Theta(1)\). Si l'on note \(T(n)\) la complexité de cet algorithme, on obtient directement la formule récurrente \begin{equation} T(n)=\begin{cases} \Theta(1),&\text{si}\ n=1,\\ aT(\frac{n}{b})+f(n),&\text{sinon.} \end{cases} \end{equation} Nous allons estimer cette fonction \(T(n)\) et pour simplifier les calculs, nous supposerons tout d'abord que \(n\) est une puissance de \(b\), disons \(n=b^k\). Si nous développons l'expression de \(T(n)\), nous obtenons \begin{align*} T(n)&=a\big(aT(n/b^2)+f(n/b)\big)+f(n)\\ T(n)&=a\Big(a\big(aT(n/b^3)+f(n/b^2)\big)+f(n/b)\Big)+f(n)\ldots\\ T(n)&=a^k\Theta(1)+\sum_{i=0}^{k-1}a^if(n/b^i). \end{align*} Et si l'on exprime ce résultat en fonction de \(n\), en remarquant que \(a^{\log_bn}=(b^{\log_ba})^{\log_bn}\) soit \(a^{\log_bn}=n^{\log_ba}\) en permutant les exposants, on arrive à \begin{equation}\label{eqrecTn} T(n)=\Theta(n^{\log_ba})+{\color{yellow}\sum_{i=0}^{\log_bn-1}a^if(n/b^i)}. \end{equation}

Pour obtenir ce résultat, on aurait également pu utiliser l'arbre de récursion associé à l'exécution de l'algorithme. La profondeur de cet arbre est évidemment \(\log_bn-1\). Pour poursuivre ce calcul, il devient nécessaire de faire des hypothèses sur la nature de la fonction \(f\). Il apparaît clairement que le résultat, sans même le connaître, dépend essentiellement du comportement de \(f(n)\) par rapport à la fonction \(n\mapsto n^{\log_ba}\). Pour la suite nous allons noter \(\color{yellow}S\) la somme de l'équation (\ref{eqrecTn}).

Nous allons étudier trois situations :

Cas 1. \(f(n)=O(n^{\log_ba-\epsilon})\), avec \(\epsilon>0\). La somme \(S\) est donc majorée : \begin{align*} S&\leq\sum_{i=0}^{\log_bn-1}a^i\left(\frac{n}{b^i}\right)^{\log_ba-\epsilon}\\ &=n^{\log_ba-\epsilon}\sum_{i=0}^{\log_bn-1}\left(\frac{ab^\epsilon}{b^{\log_ba}}\right)^i\\ &=n^{\log_ba-\epsilon}\sum_{i=0}^{\log_bn-1}b^{i\epsilon} \end{align*} En sommant la série géométrique on aboutit à \begin{align*} S&\leq n^{\log_ba-\epsilon}\left(\frac{b^{\epsilon\log_bn}-1}{b^\epsilon-1}\right)\\ &=n^{\log_ba-\epsilon}\left(\frac{n^\epsilon-1}{b^\epsilon-1}\right)\\ &=\frac{1}{b^\epsilon-1}\left(n^{\log_ba}-n^{\log_ba-\epsilon}\right) \end{align*} Comme \(1/(b^\epsilon-1)\) est une constante, on peut conclure en disant que la somme \(S\) est majorée par une constante fois \(n^{\log_ba}\) et par conséquent déterminer la classe de la fonction de complexité : \(T(n)=O(n^{\log_ba})\).

Cas 2. \(f(n)=\Theta(n^{\log_ba})\). Si on remplace dans la somme \(S\), la fonction \(f\) par \(n\mapsto n^{\log_ba}\), on obtient une quantité \(S'\) qui permet de borner \(S\). Il est en effet aisé de déduire de l'appartenance de \(f\) à la classe \(\Theta\) qu'il existe deux constantes positives \(\alpha\) et \(\beta\) telles que \(\alpha S'\leq S \leq \beta S'\). Pour éviter d'allourdir inutilement les calculs, on se contente donc d'évaluer la quantité \(S'\). On a \begin{align*} S'&=\sum_{i=0}^{\log_bn-1}a^i\left(\frac{n}{b^i}\right)^{\log_ba}\\ &=n^{\log_ba}\sum_{i=0}^{\log_bn-1}\left(\frac{a}{b^{\log_ba}}\right)^{i}\\ &=n^{\log_ba}\sum_{i=0}^{\log_bn-1}1\\ &=n^{\log_ba}\log_bn. \end{align*} En réinjectant ce résultat dans les deux inégalités issues de (\ref{eqrecTn}), on conclut avec

\[T(n)=\Theta(n^{\log_ba}\log_bn).\]

Cas 3. Il existe \(c<1\) tel que pour tout \(n\geq b\), \(af(n/b)\leq cf(n)\). C'est le cas où le coût de la récursivité est plus faible que celui du calcul intra algorithme. Dans un premier temps, l'expression de la somme \(S\) nous permet immédiatement d'affirmer que \(S=\Omega(f(n))\). Introduisons l'hypothèse dans l'expression de \(S\) : \[\leq\sum_{i=0}^{\log_bn-1}c^if(n)=f(n)\sum_{i=0}^{\log_bn-1}c^i.\] La somme de la série géométrique vaut \((1-c^{\log_bn})/(1-c)\) et comme \(c<1\) cette somme est inférieure à \(1/(1-c)\) et par conséquent \(S=O(f(n))\). Pour montrer que \(T(n)=\Theta(f(n))\), il reste un petit travail qui fait l'objet de l'exercice suivant.

Montrez que s'il existe une constante \(c\lt 1\) telle que \(af(n/b)\lt cf(n)\) pour \(n\) suffisamment grand, alors il existe une constante \(\epsilon > 0\) telle que \(f(n)=\Omega(n^{\log_ba+\epsilon})\). Concluez alors le cas 3 en montrant que \(T(n)=\Theta(f(n))\).

Il nous reste maintenant à généraliser ces trois résultats dans le cas où \(n\) n'est pas une puissance entière de la base \(b\). Nous allons étudier brièvement le cas où l'appel se fait sur \(\lceil n/b\rceil\), l'autre cas étant similaire. À chaque appel récursif, l'argument \(n\) passe à \(\lceil n/b\rceil\), puis \(\lceil\lceil n/b\rceil/b\rceil\) et \(\lceil\lceil\lceil n/b\rceil/b\rceil/b\rceil\) et ainsi de suite... Il faut donc déterminer au bout de combien d'appels le paramètre est strictement inférieur à \(b\).

En posant \(n_i=n\) si \(i=0\) et \(n_i=\lceil n_{i-1}/b\rceil\) sinon, on montre que \(n_i=\lceil n/b^i\rceil\). D'autre part, comme \(\log_bn<\lfloor\log_bn\rfloor+1\) on a \(n\lt b.b^{\lfloor\log_bn\rfloor}\) d'où \(n/b^{\lfloor\log_bn\rfloor}\lt b\) et finalement \(\lceil n/b^{\lfloor\log_bn\rfloor}\rceil\lt b\) car \(n/b^{\lfloor\log_bn\rfloor}=\lceil n/b^{\lfloor\log_bn\rfloor}\rceil\). Le nombre d'appels récursifs hormis le premier appel est donc égal à \(\lfloor\log_bn\rfloor.\) Il suffit donc de remplacer \(\log_bn\) par \(\lfloor\log_bn\rfloor\) dans la sommation de l'équation (\ref{eqrecTn}). Nous laissons au lecteur le soin de refaire les calculs avec cette nouvelle borne.

Soient \(a\geq 1\) et \(b > 1\) deux constantes, et \(f:{\N}\rightarrow {\N}\). Soit \(T:{\N}\rightarrow {\N}\) une fonction définie par la récurrence suivante : \begin{equation} T(n)=\begin{cases} \Theta(1)&\text{si}\ n=1,\\ aT(n/b)+f(n) &\text{sinon}. \end{cases} \end{equation} où \(n/b\) désigne soit l'entier \(\lfloor n/b\rfloor\) soit l'entier \(\lceil n/b\rceil\). Alors la fonction de complexité \(T\) peut être bornée asymptotiquement de la façon suivante :
  1. Si \(f(n)=O(n^{\log_ba-\epsilon})\) pour une certaine constante \(\epsilon>0\), alors \(T(n)=\Theta(n^{\log_ba})\) ;
  2. Si \(f(n)=\Theta(n^{\log_ba})\), alors \(T(n)=\Theta(n^{\log_ba}\log_bn)\) ;
  3. Si \(f(n)=\Omega(n^{\log_ba+\epsilon})\) pour une certaine constante \(\epsilon>0\) et s'il existe \(c<1\) telle que \(af(n/b)\leq cf(n)\) pour \(n\) suffisamment grand, alors \(T(n)=\Theta(f(n))\).
Ce résultat général de complexité est connu sous le nom de Master Theorem dans la littérature anglo-saxonne. Il ne traite pas tous les types de récurrences que l'on peut rencontrer en algorithmique. Le théorème d'Akra-Bazzi, établi en 1998 généralise ce théorème.