
Fig. 8. Lecture laser du disque compact.
Généralités.
Nous avons vu au paragraphe précédent que la fréquence d'échantillonnage du disque compact était de 44100Hz sur 16 bits pour chaque canal, il faut donc 44100 × 16 × 2 = 1.411.200 bits pour représenter une seconde de signal audio. On est encore très loin du nombre de bits qui seront réellement inscrits sur le disque. Nous allons décrire très brièvement les étapes que vont franchir les échantillons jusqu'à la gravure, puis nous exposerons en détail chacune de ces phases.
On segmente tout d'abord le flot binaire (bit stream) généré par la quantification, en paquets de 6 échantillons, appelés trames. On a donc 6 × 16 × 2 = 192 bits dans chaque trame. On appelera désormais symbole une séquence de huit bits. Une trame contient donc 24 symboles. Chaque trame va subir un certain nombre de transformations, la première est nécessaire pour pouvoir corriger des erreurs éventuelles au moment de la reconstitution du signal. Elle est réalisée par un code C.I.R.C. (Cross Interleave Reed-Solomon Code) dont le fonctionnement sera décrit en détail au paragraphe suivant. Très schématiquement, on ajoute tout d'abord quatre symboles de parité à la trame, puis on entrelace les 28 symboles, on ajoute à nouveau 4 symboles de parité, et on termine par un deuxième entrelacement. A cette étape une trame contient donc 32 symboles.
On ajoute un symbole appelé Control & Display (C&D), contenant les informations nécessaires à l'affichage des durées, et quelques bits inutilisés, qui pourront servir pour des applications futures. La trame comporte maintenant 33 symboles de huit bits et il n'y a a priori plus rien à ajouter au message pour l'inscrire sur le support. Pourtant le signal numérique va être modifié (plus précisement modulé) avant d'être inscrit sur le disque. Nous allons décrire maintenant le mécanisme de la lecture optique du disque par un faisceau laser, pour mettre en évidence les problèmes qui ont motivé le codage d'enregistrement E.F.M. (Eight to Fourteen Modulation).
Le disque compact se présente, comme son nom le laisse entendre, sous forme d'un disque de faible diamètre, 12cm exactement, et de 1,2mm d'épaisseur. Son poids est compris entre 14g et 33g et le diamètre du trou central est de 15mm. L'information inscrite sur le disque se présente sous la forme de créneaux constitués alternativement de bosses (bumps) et de plages lisses (lands), dont la longueur varie entre 0.9025µm et 3.307µm, dont la largeur est de 0.6µm et la hauteur de 0.12µm. Ces bosses et ces plages lisses existent en neuf longueurs distinctes, donc contrairement à certaines suppositions, le signal n'est pas codé selon un mode ``tout ou rien''. De la même manière que pour le sillon d'un disque analogique, le créneau est enroulé en spirale entre un diamètre de 46mm et un diamètre de 117mm, mais la lecture se fait du centre vers les bords.

Pour fabriquer un disque compact, on grave sur un disque maître (master), le créneau ``inverse'' (un peu comme un négatif en photographie) de celui que l'on trouvera ensuite sur un disque. Cette gravure est réalisée par le passage d'un spot laser sur le disque maître préalablement recouvert d'une couche photorésistive. Après développement et métallisation de la surface, on obtient des cuvettes (pits), donc en creux, et c'est ce disque qui servira à la fabrication en série des disques compacts moulés par injection de polycarbonate, puis métallisés, recouverts d'une couche de protection, découpés et enfin sérigraphiés.
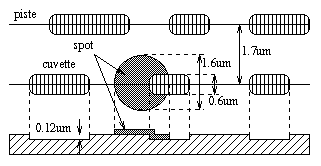 |
La lecture se fait à l'aide d'un spot laser d'une longueur d'onde de départ de 780nm. Ce spot est focalisé par un système de lentilles, traverse un miroir sans tain et arrive au niveau de la surface embossée avec un diamètre de l'ordre de 1.6µm (figure 9). Sur les plages lisses, le rayon est réfléchi à 90% (la perte est due à la diffraction et aux matériaux) puis récupéré par un jeu de cellules réceptrices après réflexion sur le miroir. Dans le cas d'une bosse, la valeur est comprise entre 65 et 75%, et pas nulle comme on pourrait le penser. Pour déterminer la durée de lecture d'un disque, on pourrait considérer qu'elle dépend de la longueur de la piste, et de la densité d'information que l'on peut inscrire sur cette piste. Nous allons plutôt considérer qu'elle dépend de la longueur de la piste et de la vitesse de lecture v. Ce point de vue est strictement équivalent, si ce n'est qu'il fait intervenir v, et ce paramètre est essentiel dans ce qui va suivre. Cette vitesse linéaire v de balayage de la piste est constante, ainsi c'est la vitesse angulaire qui varie entre 150 et 530 tours/minute de manière à garder v constante.
Un autre paramètre essentiel dans tout ce qui va suivre est le diamètre d du spot laser. Il va déterminer la résolution du système, autrement dit sa capacité à distinguer des détails très petits sur le disque. Un des buts à atteindre pour la réalisation du système est évidemment de maximiser la durée de lecture en respectant les différentes contraintes physiques. Plus la vitesse de lecture est faible, i.e. plus la densité d'information est grande, plus cette durée sera importante. Nous allons montrer comment calculer cette vitesse, et surtout comment on peut la réduire à l'aide d'un codage approprié des symboles de la trame.
Il est important de signaler que de nombreux paramètres entrent en jeu dans cette détermination et qu'ils sont tous dépendants les uns des autres. Il est donc impossible de les décrire en séquence, ce qui complique sensiblement l'exposé. On peut tout d'abord déterminer très facilement la longueur de la piste. La largeur d'une cuvette est de 0.6µm et le diamètre du spot laser d'environ 1.6µm. L'écartement entre deux enroulements est donc au moins de la même valeur. On connait la taille de la bande circulaire utile, et on obtient environ 5km de piste. Pour déterminer la vitesse v, on va tout d'abord se placer dans une situation de référence où il n'y a pas de code d'enregistrement. Une bosse sera interprétée comme un 1 et une cuvette comme un zéro (ou vice-versa).
Remarque: Les normes ont été fixées par Philips dans le red book [20]:
| DISQUE | |
|---|---|
| Durée d'exécution: | 74 minutes, 33 secondes maximum |
| Sens de rotation: | Sens des aiguilles d'une montre vue de la surface de lecture |
| Vitesse de rotation | 1.2 - 1.4 m/sec. (vitesse linéaire constante) |
| Largeur de la piste: | 1.6 µm |
| Diamètre: | 120 mm |
| Epaisseur: | 1.2 mm |
| Diamètre du trou central | 15 mm |
| Zone d'enregistrement: | 46 mm - 117 mm |
| Région du signal: | 50 mm - 116 mm |
| Support: | Tout support avec un indice de réfraction de 1.55 |
| Longueur minimale du crénau: | 0.833 µm (1.2 m/sec) à 0.972 µm (1.4 m/sec) |
| Longueur maximale du crénau: | 3.05 µm (1.2 m/sec) à 3.56 µm (1.4 m/sec) |
| Profondeur du créneau: | ~0.11 µm |
| Largeur du créneau: | ~0.5 µm |
| SYSTEME OPTIQUE | |
| Longueur d'onde standard: | 780 nm (7,800 Å) |
| Profondeur de focale: | ± 2 µm |
| FORMAT DU SIGNAL | |
| Nombre de canaux: | 2 canaux (enregistrement sur 4 canaux possible) |
| Quantification: | 16-bit linéaire |
| Fréquence d'échantillonage: | 44.1 kHz |
| Rendement binaire du canal: | 4.3218 Mb/sec |
| Rendement des données: | 2.0338 Mb/sec |
| Rapport données/canal: | 8:17 |
| Code correcteur d'erreurs: | Cross Interleaved Reed-Solomon Code |
| Code d'enregistrement: | Eight-to-Fourteen Modulation (EFM) |
Un premier codage.
Les résultats énoncés dans ce paragraphe sont largement inspirés de l'ouvrage de Kees A. Schouhamer Immink, Coding Techniques for Digital Recorders [18].
La lecture par le spot laser de la piste engendre un courant à la sortie des cellules réceptrices. Les variations d'amplitude de ce courant sont obtenues à chaque transition (``mur''). On devrait donc récupérer un signal similaire aux créneaux. On obtient en fait un signal en forme de vagues dont la fréquence dépend de la fréquence ft des transitions. La fréquence fs la plus haute du signal est obtenue avec le symbole 10101010 (ou son complémentaire). Dans ce cas particulier on a exactement une sinusoîde de période Ts double de celle des transitions Ts. (figure 10 (c)).
La fréquence d'horloge du lecteur étant synchronisée sur la fréquence du flot binaire fb (dans ce cas particulier égale à ft), on obtient, non pas une sinusoîde, mais la superposition des signaux générés par les transitions successives entre cuvettes et bosses. La courbe résultante en forme de losanges est appelée diagramme de l'oeil (figure 10 (d)).
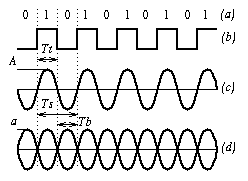 |
Si le signal est suffisamment précis, il est toujours possible à chaque période Tb du signal de déterminer sur ce diagramme si le signal est positif ou non, et donc de reconstituer la séquence binaire associée.
Le diagramme de l'oeil peut-être perturbé par une mauvaise focalisation du spot laser, ou une surface abîmée. L'amplitude A du signal en sera donc affectée, et si elle devient trop faible, c'est-à-dire si elle est inférieure à un certain seuil appelé seuil de décision, on ne pourra plus reconstituer le message. On associe à cette valeur A la demi-hauteur de l'oeil a. Dans la situation de référence actuelle a = A. L'amplitude A du signal dépend de la fréquence de transition ft, donc de la vitesse de lecture v. On a pu simuler à l'aide d'une analyse de Fourier la fonction A(fs) déterminant l'amplitude du signal, en fonction de sa fréquence fs.
Cette fonction dépend du diamètre d du spot laser et de la vitesse v. Ces deux paramètres définissent une fréquence de coupure fc au delà de laquelle l'amplitude du signal capté est nulle. Cette fréquence est déterminée par la formule fc = v/d dans le cas d'une optique et d'une réception parfaites. La situation réelle sera naturellement moins favorable. La courbe de la fonction A est une droite passant par les points (0,1) et (fc,0), où l'amplitude a été normalisée (fig. 11). La pente de la droite dépend donc de la vitesse v. Pour une amplitude A fixée, on peut déterminer la fréquence de coupure fc, de manière à ce que A soit l'image de la fréquence maximale fs du signal.
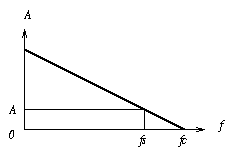 |
Si A est faible on pourra sensiblement approcher fc de fs c'est-à-dire de fb/2. La fréquence de transition la plus haute est déterminée par la période Tt associée (minimum run length), autrement dit, la longueur minimale entre deux transitions. Cette longueur dépend évidemment de la résolution du spot laser, donc de son diamètre.
On va maintenant considérer une situation voisine du codage E.F.M. qui va permettre de diminuer la vitesse v et ainsi d'augmenter la durée de lecture. On augmente la longueur minimale entre deux transitions d'un facteur de 3/2 par rapport à la situation de référence ci-dessus, et on convertit les symboles de 8 bits en mots de 16 (modulation 8-16) de manière à ce que l'on trouve toujours au moins trois 0 ou trois 1 consécutifs (cette situation n'est pas très éloignée du codage E.F.M., voir figure 12). Ce codage est réalisé à l'aide d'une table de transcodage, et il y a bien sûr bijection entre les 256 symboles possibles et leurs codes.
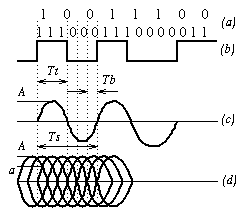 |
Une bosse peut désormais ``porter'' trois bits, et la fréquence du flot binaire est à présent différente de la fréquence de transition. On a ft = fb / 3 et donc fs = ft / 2 = fb / 6. Si on suppose qu'une faible demi-hauteur de l'oeil est acceptable, la fréquence de coupure, donc la vitesse v, a été réduite d'un facteur de 3/2 par rapport à la fréquence de coupure précédente. Ceci représente un gain de 50% de la durée de lecture. Ce codage s'est fait au prix d'une diminution de moitié de la demi-hauteur de l'oeil, ceci n'est donc réalisable que si cette hauteur est acceptable.
Comme on peut l'imaginer, d'autres systèmes ont été testés, par exemple une modulation 8-24, mais il s'avère que la modulation 8-16 est le compromis le plus satisfaisant en situation réelle, en tenant compte du fait que la fréquence de coupure est de 20% inférieure à la valeur idéale de v/d. Ce codage est meilleur non seulement en termes quantitatifs, mais aussi en termes qualitatifs. En effet, expérimentalement, la demi-hauteur de l'oeil est moins sensible aux effets de défocalisation qu'avec les autres codes.
Nous allons voir qu'il y a d'autres contraintes à respecter pour la lecture du disque, et ceci va nous amener à considérer un codage d'enregistrement voisin du codage 8-16, le codage E.F.M.
Le codage E.F.M.
Nous avons vu avec le codage 8-16, que la cuvette (ou la bosse) la plus petite était de longueur 3 × Tb. Par contre la longueur la plus grande entre deux transitions n'avait aucune limitation. La longueur minimum effective est Tmin = 0.9025µm, c'est donc trois fois la période Tb = 0.3008µm. La réalisation d'un disque et d'un lecteur exige des tolérances de fabrication, entre autres, sur l'excentrage du trou central, le poids du disque, l'épaisseur du disque, le voile éventuel, la focalisation du spot laser, la position des ``murs'' de transition, la profondeur des cuvettes, etc..., la liste est bien sûr loin d'être exhaustive.
Ainsi, la longueur des cuvettes et des bosses peut plus ou moins varier autour d'une longueur de référence. La fréquence d'horloge du lecteur sur laquelle est basé le ``découpage'' Tb de la piste n'est pas non plus d'une précision infinie, il en résulte une erreur de synchronisation à chaque impulsion. L'erreur commise peut se propager au fur et à mesure de la lecture, il faut alors synchroniser suffisamment souvent le lecteur de manière à ce que le nombres de bits lus ne soit pas erroné. Les différentes tolérances déterminent la longueur maximale (maximum run length) entre deux transitions, elle est de 11 fois la période Tb, i.e. Tmax = 11 × Tb. L'horloge est synchronisée à chaque transition.
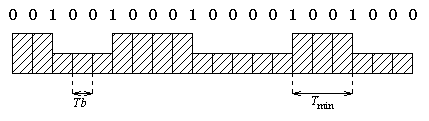
Il est indispensable qu'à toute position sur la piste on ne trouve jamais deux transitions éloignées de plus de 11 × Tb. Cette contrainte entraîne un codage approprié. La première différence entre le code E.F.M. et le code 8-16 est la façon d'interpréter les bosses et les creux. Chaque transition est maintenant lue comme un 1 et la distance entre deux transitions détermine le nombre de zéros entre deux 1 (figure 13). Ceci ne change absolument rien à l'étude faite au paragraphe précédent. La premi ère contrainte obtenue avec le codage 8-16, à savoir Tmin = 3 × Tb, s'interprète maintenant comme ``au moins 2 zéros entre deux un'', et la contrainte précédente Tmax = 11 × Tb comme ``au plus 10 zéros entre deux un''.
 |
On peut considérer que le flot binaire - le bit stream - est une suite binaire infinie, on donne alors la définition suivante:
Définition On dit qu'une suite binaire (un) suit la contrainte (d,k) ou encore que la suite est une (d,k)-séquence, si elle vérifie les deux conditions suivantes:
Le problème qui se pose maintenant est de transformer le flot binaire en une (2,10)-séquence. En général on cherche à construire un transducteur (automate d'états finis) réalisant le codage adéquat, mais dans le cas du disque compact, ce n'est pas cette approche qui a été retenue car le flot binaire est segmenté en trames, et on voulait transcoder successivement les symboles de la trame. On cherche donc une bijection de {0,1}8 dans une partie P de {0,1}n où n est à déterminer de manière à ce qu'il y ait suffisamment de mots dans {0,1}n qui vérifient la contrainte (2,10) pour qu'on puisse en extraire une partie P de cardinal 256. Un simple calcul de dénombrement montre que l'on peut construire 267 mots de longueur 14 vérifiant la contrainte (2,10). Il y a donc 11 mots supplémentaires. Une partie de la table de transcodage est donnée dans le tableau 3.
| Index | Symbole (8 bits) | Code (14 bits) |
|---|---|---|
| 100 | 01100100 | 01000100100010 |
| 101 | 01100101 | 00000000100010 |
| 102 | 01100110 | 01000000100010 |
| 103 | 01100111 | 00100100100010 |
| 104 | 01101000 | 01001001000010 |
| 105 | 01101001 | 10000001000010 |
| 106 | 01101010 | 10010001000010 |
| 107 | 01101011 | 10001001000010 |
| 108 | 01101100 | 01000001000010 |
| 109 | 01101101 | 00000001000010 |
Ce codage, s'il associe bien à un symbole un mot vérifiant la contrainte (2,10), ne permet pas de générer une (2,10)-séquence par concaténation des mots codés sur 14 bits. En effet, les mots 01000100000000 et 00000001000010 vérifient bien la contrainte (2,10), mais leur concaténation donne :
Il y a 16 zéros consécutifs, ce qui est interdit. Pour pallier à ce problème on va intercaler 3 bits qui vont servir à lier les mots entre eux, il faut donc mémoriser deux symboles avant de les inscrire. Parmi les 8 mots de liaison possibles, seuls 4 sont autorisés: 000, 100, 010, 001. Pour l'exemple ci-dessus, on pourrait lier les deux mots par 100, 010, ou 001.
Parmi les 11 mots qui ne serviront pas à coder les symboles, on a éliminé tous ceux qui présentaient une longue séquence de zéros en début ou en fin de mot. En effet, même avec trois bits de liaison, on ne peut lier deux mots comportant respectivement 10 zéros en fin et en début de mot. C'est ainsi que l'on a écarté les 4 mots comportant 10 zéros en début ou en fin de séquence, et les 6 mots en comportant 9. Le circuit de décodage, autrement dit le choix de la bijection, a été optimisé sur ordinateur de manière à être réalisé avec le nom bre minimum de portes logiques. C'est de cette manière que l'on a écarté le dernier mot.
On remarque aisément qu'avec les 256 mots choisis pour le codage on aurait pu se contenter de 2 bits de liaison. Le troisième bit, a priori superflu, donne plus de liberté dans le choix de la liaison. Ceci va être déterminant pour minimiser un phénomène tr ès gênant pour la lecture du disque.
Les servo-systèmes qui gèrent le suivi de la piste sont controlés par des signaux à fréquences basses, or le signal de sortie contient lui aussi des basses fréquences (celles présentes dans le diagramme de l'oeil), il peut donc y avoir des interférences. D'autre part, nous avons vu que dans le cas d'un disque sale ou présentant des empreintes de doigts, l'amplitude du signal peut décroitre sous le seuil de décision. Il s'avère que ce phénomène est en partie minimisé en filtrant les basses fréquences. Ceci n'est évidemment possible que dans le cas où le signal ne contient pas d'information à ces fréquences.
Il est cependant impossible de filtrer toutes les composantes en basse fréquence sans perdre de l'information. Le filtre passe-haut doit donc être un juste compromis entre ces deux phénomènes contradictoires. Nous avons vu que le diagramme de l'oeil était la superposition de tous les signaux successifs générés par les différentes transitions sur la piste. On peut mesurer le contenu en basses fréquences du signal à l'aide d'un paramètre appelé R.D.S. (Run Digital Sum), ou somme digitale courante. Il s'agit de la différence entre la longueur cumulée des cuvettes, et la longueur cumulée des bosses, où l'unité de longueur est la période du signal binaire Tb.
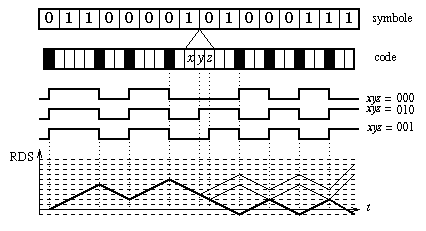
On peut donc diminuer les composantes en basses fréquences en essayant de ramener la R.D.S. au voisinage de 0. C'est pour cela que l'on se donne trois bits de liaison, et on choisit parmi les liaisons possibles, celle qui minimisera la valeur absolue de la R.D.S. en ne considérant qu'un symbole ``en avant'' du symbole courant. L'exemple de la figure 14 montre comment on a déterminé la séquence 000 pour la liaison des codes 10000100100010 (du symbole 01100001) et 00100100100100 (du symbole 01000111). Dans le système du disque compact, l'application de cette technique entraîne une diminution du bruit d'environ 10 décibels dans la bande de fréquence des servos-systèmes (0 à 20kHz).
 |
Il reste un dernier problème à résoudre, celui de la synchronisation, non plus de la fréquence d'horloge, mais du décodage du signal sur la piste. En effet, si les symboles des trames successives étaient inscrits à la suite, après le codage E.F.M. et l'adjonction des trois bits de liaison, le moindre saut de piste empêcherait de retrouver où commencer l'interprétation d'un mot. On remédie à cela en inscrivant sur le disque une séquence de synchronisation répétée à intervalles réguliers. Cette séquence est justement construite à partir d'un des onze mots que l'on avait rejeté parmi les 267 mots possibles du code E.F.M. La séquence est :
>1000000000010000000000xyztu
On répète donc deux fois la séquence composée d'un 1 suivi de 10 zéros, et xyztu désignent les cinq bits nécessaires à minimiser la R.D.S., déterminés de la même façon que pour l'exemple précédent. Cette séquence est placée au début de chaque trame de 33 symboles. En fait la longueur des trames a été déterminée de manière à ce que la synchronisation puisse se faire suffisamment souvent.
On peut maintenant conclure en déterminant le nombre d'informations finalement inscrites sur le disque. On était parti d'une trame de 24 symboles, c'est-à-dire 6 échantillons de 32 bits, et on a ajouté apr ès le codage correcteur, 8 symboles de parité et un symbole de contrôle C&D. La trame contient donc 33 symboles, et chacun de ses symboles est codé à l'enregistrement sur 14 bits par le codage E.F.M. On ajoute entre deux mots de 14 bits, 3 bits de liaison, et pour chaque trame, autrement dit tout les 33 symboles, on inscrit 27 bits de synchronisation.
On a donc pour 192 bits d'information audio-numérique, un codage final comportant 588 bits (33 × (14 + 3) + 27). Une trame correspondant à 6 échantillons, il faut donc 588 × 44100 / 6 = 4.321.800 bits pour une seconde de musique, soit 3 fois plus que ce qui était nécessaire pour la quantification.
Remarque: On peut améliorer la minimisation de la R.D.S. en considérant plus d'un symbole après le symbole courant, mais cela n'a pas été implémenté sur le disque compact.
Nous allons donner à titre indicatif un code d'enregistrement beaucoup plus performant que le code E.F.M. sur la plupart des critères requis par le disque compact.
Le code (2,7) de P.A. Franaszek.
P.A. Franaszek a conçu ce code pour l'enregistrement sur disque des fichiers informatiques (IBM 3370/3380). C'est un code particulier où la segmentation de la suite binaire d'entrée n'est pas à longueur fixe (8 bits pour le codage E.F.M.), mais à longueur variable (table 4).
| Entrée | Sortie | Sortie |
|---|---|---|
| 10 | ac | 0100 |
| 11 | bc | 1000 |
| 011 | cbc | 001000 |
| 010 | bac | 100100 |
| 000 | cac | 000100 |
| 0011 | ccbc | 00001000 |
| 0010 | cbac | 00100100 |
Exemple: Le mot 1001101011 est codé:
| Entrée: | 10 | 011 | 010 | 11 |
|---|---|---|---|---|
| Sortie: | ac | cbc | bac | bc |
Ce code génère des (2,7)-séquences à partir d'une suite binaire quelconque. La contrainte (2,10) du disque compact est donc largement vérifiée, et ce code permettrait de synchroniser plus fréquemment l'horloge du lecteur. Un autre avantage non négligeable est le circuit de décodage extrêmement simple, il suffit d'un registre à décalage sur 8 bits, avec un décalage de deux, synchronisé sur la période du canal binaire. A chaque cycle, le bit de sortie b est calculé à l'aide de l'expression booléenne:
où xi, 0 < i < 9, désigne le ième bit du registre et xi = ¬xi. Le circuit est donc réalisé par un nombre très restreint de portes logiques. L'expression booléenne ci-dessus montre que la propagation d'une erreur sur un bit en entrée est limitée à quatre bits en sortie.
Nous avons vu que le codage E.F.M. nécessitait une synchronisation à chaque trame pour déterminer où commencer l'interprétation. Le code de Franaszek permet de corriger automatiquement une erreur de synchronisation éventuelle. Regardons l'exemple suivant: Le mot 1011010011 est codé
| Entrée: | 10 | 11 | 010 | 011 |
|---|---|---|---|---|
| Sortie: | ac | bc | bac | cbc |
La segmentation des deux suites dans cette table est primordiale pour le codage et le décodage. Nous allons voir que l'on peut commencer l'interprétation de la (2,7)-séquence au mauvais moment et ``retomber sur ses pieds''. Imaginons que l'on commence le décodage à partir de la deuxième lettre, la table 4 nous indique la segmentation et le décodage:
| Entrée: | cbc | bac | cbc |
|---|---|---|---|
| Sortie: | 011 | 010 | 011 |
On retrouve la bonne position, dans ce cas précis, dès la deuxième interprétation. On peut montrer que cette propriété est vérifiée dans n'importe quel cas de figure. Ainsi, si le code de Franaszek était implémenté dans le système du disque compact, on éviterait les 27 bits de synchronisation.
La contrainte k = 7 qui permettrait de synchroniser plus souvent l'horloge du lecteur, pourrait aussi minimiser les conséquences d'un phénomène optique très gênant. Le faisceau laser arrive perpendiculairement à la surface du disque, traverse le polycarbonate, et se focalise progressivement pour atteindre un diamètre de 1.6µm au niveau de la piste. L'indice de réfraction du polycarbonate étant de 1.55 contre 1 pour l'air, la longueur d'onde du spot laser passe de 800nm à 500nm environ. Si le disque est voilé, même très faiblement, la direction du faisceau est modifiée de manière sensible, de la même façon que pour un bâton que l'on enfonce dans l'eau. Les conséquences de ce phénomène sont dramatiques, les bosses n'ont plus la même longueur apparente, et cela introduit des erreurs d'interprétation. Des mesures montrent qu'une erreur d'inclinaison aussi faible que 0.6o suffit à multiplier par 100 voire par 1000 les erreurs de lecture! Ces erreurs d'interprétation se font plus souvent sur des bosses ou des cuvettes de grande longueur, c'est pour cela que le code de Franaszek, qui limite la longueur à 8 périodes, pourrait réduire légèrement ce phénomène.
En conclusion, non seulement le code de Franaszek est meilleur sur de nombreux critères, mais en plus il permettrait d'augmenter la durée de lecture. On coderait directement le flot binaire provenant du codage correcteur, le rendement du code d'enregistrement étant de 1/2, il faudrait donc 16 × 33 = 528 bits pour une trame. Cela représente un gain de 8 minutes par rapport au codage E.F.M. Le seul défaut de ce code c'est qu'il ne permet pas de minimiser la R.D.S., donc de contrôler les basses fréquences du signal. Au regard de ses excellentes propriétés, il faut croire que la contrainte de minimisation de la R.D.S. est essentielle pour le bon fonctionnement du système.
Remarques: Le faisceau laser est aussi réfléchi
par les bords du disque, particulièrement sur ceux des disques récents,
perpendiculaires au plan du disque, alors que les premiers étaient
arrondis. Cela entraîne un parasitage lumineux qui peut se corriger
à l'aide d'un traitement adéquat des bords du disque. Il
suffit de passer un feutre indélébile vert Lumocolor 357
Staedler (voir [7]).
On peut constater une amélioration sensible de la qualité
d'écoute en superposant deux disques, le disque supérieur
faisant office de palet presseur stabilisateur par effet de coussin d'air.
Ceci permet de diminuer le voile éventuel du disque lu et de réduire
les vibrations.