Quelques définitions
On rappelle (voir ordre lexicographique) que si \(A\) est un alphabet fini, \(A^*\) désigne la fermeture de Kleene de \(A\), c'est-à-dire l'ensemble des séquences (suites finies) de symboles de \(A\) que l'on appelle mots. Cet ensemble est muni d'une loi de composition interne \(\cdot\) appelée concaténation, on inclut dans \(A^*\) le mot vide \(\varepsilon\) qui est l'élément neutre pour cette loi. Par exemple avec l'alphabet \(A:=\{0, 1\}\), on a \(A^*=\{\varepsilon,0,1,00,01,\ldots\}.\) Le nombre de symboles d'un mot \(u\) est appelé longueur du mot que l'on note indifféremment \(|u|\) ou \(\#u\). On appelle langage sur l'alphabet \(A\) tout sous-ensemble \(L\) de \(A^*\). On étend la loi de concaténation entre mots de \(A^*\) aux mots de deux langages \(L,M\subseteq A^*\) par \begin{equation} L.M:=\{u.v\ |\ u\in L\ \text{et}\ v\in M\}. \end{equation} Par abus de langage, si \(s\in A^*\) et \(L\subseteq A^*\), on note \(s.L\) l'ensemble \(\{s\}.L\) et \(L.s\) l'ensemble \(L.\!\{s\}\).
En mathématique, une sous-séquence \(u\) d'un mot \(v\) est aussi appelée suite extraite de \(v\). Concrètement \(u\preceq v\) signifie que l'on peut retrouver chaque symbole de \(u\) dans le mot \(v\) et dans le sens de lecture.
Les deux lemmes suivants sont faciles à établir et seront utiles pour démontrer le résultat principal sur lequel s'appuie l'algorithme.
Présentation du problème et première partie de l'algorithme
En bio-informatique l'étude du génome amène les chercheurs à comparer des brins d'adn. Un brin d'adn est constitué exclusivement de 4 nucléotides dont l'assemblage moléculaire est caractéristique du brin. On le modélise très facilement comme un mot sur l'alphabet \(\{A, C, G, T\}\) dont les symboles désignent respectivement les nucléotides Adénine, Thymine, Cytosine et Guanine. Il faut trouver un outil adéquat pour comparer les brins ou en trouver les points communs. Dans un autre registre, comment mesurer la similitude entre deux fichiers informatiques (commande diff du système unix), ou encore quel est le mot le plus proche d'un mot donné ? Toutes ces interrogations trouvent une réponse possible avec la recherche des plus longues sous-séquences communes.
L'objectif est d'écrire un algorithme efficace pour chercher les plus longues sous-séquences communes de deux séquences données \(u\) et \(v\). Une approche naïve est possible, on peut par exemple construire toutes les sous-séquences de \(u\) et toutes les sous-séquences de \(v\) puis rechercher parmi les sous-séquences communes quelle est/sont la/les plus longue(s). Le résultat de l'exercice 1 nous incite à fuir cette approche. En effet, si on note \(U\) et \(V\) l'ensemble des sous-séquences de \(u\) et \(v\) respectivement, on sait que \(\#U=2^{|u|}\) et \(\#V=2^{|v|}\) et il faudrait donc \(2^{|u|}+2^{|v|}\) opérations pour calculer \(U\) et \(V\) dans un premier temps. Il resterait encore à calculer l'intersection \(U\cap V\) de ces deux ensembles soit \(2^{|u|}\times 2^{|v|}\) opérations supplémentaires si on comparait un-à-un les éléments de \(u\) avec ceux de \(v\), et pour finir \(\#U\cap V\) opérations pour en extraire le(s) mot(s) le(s) plus long(s). Soit au final une complexité de l'ordre de \(\Theta(2^{|u|+|v|})\) ce qui est considérable.
On peut faire mieux et nous allons opérer en deux phases. La première consiste à calculer \(\Lambda(u,v)\) et la seconde à déterminer une plsc ou toutes les plsc. Nous verrons que selon que l'on veut calculer une ou l'ensemble des plsc, la complexité de l'algorithme est très différente.
Soit \(u=u_1u_2\ldots u_n\in A^*\). On appelle équeuté de \(u\) le préfixe \(u':=u_1u_2\ldots u_{n-1}\) si \(n>1\) et \(u':=\varepsilon\) sinon. Le résultat suivant permettra de justifier l'algorithme :
On a donc \(w_k=u_n=w_m=\alpha\), montrons que \(w'\in\Pi(u',v')\). On a \(w\in\Pi(u,v)\) donc \(w\preceq u'.\alpha\) et \(w\preceq v'.\alpha\) soit \(w'.\alpha\preceq u'.\alpha\) et \(w'.\alpha\preceq v'.\alpha\) soit \(w'\preceq u'\) et \(w'\preceq v'\) d'après le lemme 3 et finalement \(w'\in\Pi(u',v')\).
2. On a \(w\in\Pi(u,v)\) donc \(w\preceq u'.u_n\) et \(w\preceq v'.v_m\). Comme \(u_n\not=v_m\), on a nécessairement \(w_k\not=u_n\) ou \(w_k\not= v_m\). Supposons que \(w_k\not=u_n\). D'après le lemme 4, on déduit que \(w\preceq u'\) et ainsi que \(w\in\Pi(u',v)\). Dans l'autre cas, le raisonnement est symétrique ce qui achève la démonstration.
Le théorème fournit immédiatement une définition récurrente de l'ensemble \(\Pi(u,v)\) et l'algorithme récursif n'est que la traduction de cette définition : \begin{equation}\label{defrec:Pi} \Pi(u,v):= \begin{cases} \varepsilon&\text{si}\ u=\varepsilon\ \text{ou}\ v=\varepsilon,\\ \Pi(u',v').u_n&\text{si}\ u_n=v_m,\\ \Pi(u',v)\cup\Pi(u,v')&\text{si}\ u_n\not=v_m. \end{cases} \end{equation}
Et il ne reste plus qu'à le traduire en algorithme :PLSCRec(u,v):liste de mots
données
u,v: mots
variables
debut
SI (u = ε OU v = ε):
retourner []
SINON SI u[#u] = v[#v]:
retourner PLSCRec(u',v').u[#u]
SINON:
retourner PLSCRec(u',v) + PLSCRec(u,v')
FIN.
Dans cet algorithme, les opérateurs \(\color{yellow}.\) et \(\color{yellow}+\) désignent respectivement la concaténation des mots et la concaténation des listes. Malheureusement sa complexité (que nous étudierons dans la section suivante) est en \(\Theta(2^{\min\{|u|,|v|\}})\) à cause des deux appels récursifs. Nous allons procéder différemment en éliminant la récursivité. On déduit immédiatement de (\ref{defrec:Pi}) un corollaire sur \(\Lambda(u,v)\) :
\begin{equation}\label{defrec:Lambda} \Lambda(u,v):= \begin{cases} 0&\text{si}\ u=\varepsilon\ \text{ou}\ v=\varepsilon,\\ \Lambda(u',v') + 1&\text{sinon et si}\ u_n=v_m,\\ \max\{\Lambda(u',v),\Lambda(u,v')\}&\text{sinon et si}\ u_n\not=v_m. \end{cases} \end{equation}L'expression (\ref{defrec:Lambda}) montre que pour calculer \(\Lambda(u,v)\) il suffit de connaître les trois quantités \(\Lambda(u',v)\), \(\Lambda(u,v')\) et \(\Lambda(u',v')\). Notons \(n:=|u|\) et \(m:=|v|\). On définit la matrice entière \(L\) de dimension \((n+1)\times (m+1)\) par \begin{equation}\label{eq:matrice} L_{i,j}:=\begin{cases} \Lambda(u_1u_2\ldots u_i, v_1v_2\ldots v_j)&\text{si}\ i>0\ \text{et}\ j>0,\\ 0&\text{sinon}. \end{cases} \end{equation}
Ainsi, si l'on calcule les termes de la matrice dans l'ordre de lecture, de gauche à droite puis de haut en bas, on dispose toujours des 3 quantités \(\color{#6464FF}\Lambda(u',v)\), \(\color{yellow}\Lambda(u,v')\) et \(\color{orange}\Lambda(u',v')\) qui sont disposées géographiquement à l'ouest, au nord et au nord-ouest et servent à calculer \(\color{red}\Lambda(u,v)\).
Exemple : On considère les mots \(u={\color{white}algorithme}\) et \(v={\color{white}larme}\) : \begin{equation} \begin{matrix} L & j & 0 & 1 & 2 &\color{red}\bf 3 & 4 & 5\\ i & & \varepsilon &\color{red} l &\color{red} a &\color{red} r &\color{white} m &\color{white} e\\ 0 & \varepsilon & 0 & 0 & 0 & 0 & 0 & 0\\ 1 &\color{red} a & 0 & 0 & 1 & 1 & 1 & 1\\ 2 &\color{red} l & 0 & 1 & 1 & 1 & 1 & 1\\ 3 &\color{red} g & 0 & 1 & 1 & 1 & 1 & 1\\ 4 &\color{red} o & 0 & 1 & 1 & 1 & 1 & 1\\ 5 &\color{red} r & 0 & 1 & \color{orange}1 & \color{#6464FF}2 & 2 & 2\\ \color{red}\bf 6 &\color{red} i & 0 & 1 & \color{yellow}1 & \color{red}\bf 2 & 2 & 2\\ 7 &\color{white} t & 0 & 1 & 1 & 2 & 2 & 2\\ 8 &\color{white} h & 0 & 1 & 1 & 2 & 2 & 2\\ 9 &\color{white} m & 0 & 1 & 1 & 2 & 3 & 3\\ 10 &\color{white} e & 0 & 1 & 1 & 2 & 3 & 4 \end{matrix} \end{equation}
La valeur \(\color{red}L_{6,3}=2\) correspondant à la longueur \(\Lambda({\color{red}algori},{\color{red}lar})\) ne dépend que des valeurs \(\color{yellow}L_{6,2}=1\), \(\color{#6464FF}L_{5,3}=2\) et \(\color{orange}L_{5,2}=1\).
LPLSC(u,v):matrice entière
données
u,v: mots
variables
L: matrice d'entiers
i,j: entiers
debut
Allouer(L,(|u|+1)*(|v|+1),0)
i ← 1
TQ i ≤ #u:
j ← 1
TQ j ≤ #v:
SI u[i] = v[j]:
L[i,j] = L[i-1,j-1] + 1
SINON:
L[i,j] = max(L[i-1,j],L[i,j-1])
j ← j + 1
i ← i + 1
renvoyer L
FIN
Deuxième partie de l'algorithme
Maintenant que nous disposons des longueurs des plus grandes sous-séquences communes, nous pouvons facilement trouver une plsc. La définition récurrente de \(\Lambda\) en (\ref{defrec:Lambda}) précise quelle règle a été appliquée pour la construction de la matrice. Réciproquement, on va construire un chemin dans la matrice \(L\) qui part de l'angle sud-est de coordonnées \(i\leftarrow|u|\) et \(j\leftarrow|v|\) pour rejoindre la ligne 0 ou la colonne 0 et reconstituer une plsc \(w\) initialisée au mot vide \(\varepsilon\) :
Deux possibilités s'offrent au point B.3 selon que l'on cherche à déterminer l'ensemble \(\Pi(u,v)\) dans son intégralité ou une plsc arbitraire. La définition (\ref{defrec:Lambda}) montre que dans ce cas elle a été obtenue indifféremment à partir de l'un des deux maximums, on peut donc continuer la construction d'une plsc par le nord ou par l'ouest. On a donc implicitement un arbre de décision.
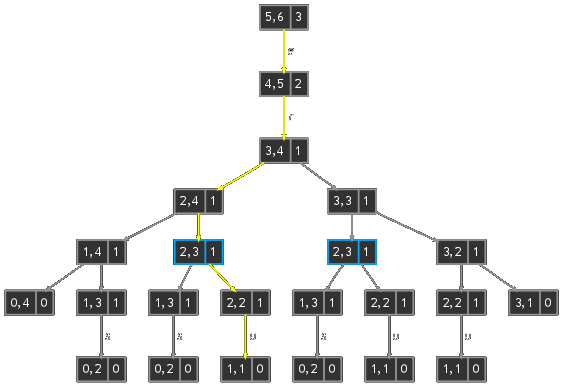
Pour comprendre cette construction, étudions le cas des séquences \(u=sucre\) et \(v=lustre\). On calcule tout d'abord la matrice \(L\) : \begin{equation} \begin{matrix} L & j & 0 & 1 & 2 &\color{red}\bf 3 & 4 & 5 & 6\\ i & & \varepsilon &\color{red} l &\color{red} u &\color{red} s &\color{red} t &\color{white} r &\color{white} e\\ 0 & \varepsilon & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 &\color{red} s & 0 & \color{yellow}\bf0 & 0 & 1 & 1 & 1 & 1\\ 2 &\color{red} u & 0 & 0 & \color{yellow}\bf1 & \color{yellow}\bf1 & \color{yellow}\bf1 & 1 & 1\\ 3 &\color{red} c & 0 & 0 & 1 & \color{#6464FF}\bf1 &\color{yellow}\bf1 & 1 & 1\\ 4 &\color{white} r & 0 & 0 & 1 & 1 & 1 &\color{yellow}\bf 2 & 2\\ 5 &\color{white} e & 0 & 0 & 1 & 1 & 1 & 2 & \color{yellow}\bf3\\ \end{matrix} \end{equation} Le chemin commence en \(\color{yellow}(5,6)\) avec \(w=\varepsilon\) et se poursuit en \(\color{yellow}(4,5)\) avec \(w=e\) puisque \(u_5=v_6=e\), continue en \(\color{yellow}(3,4)\) avec \(w=re\) puisque \(u_4=v_5=r\). À ce stade le chemin peut bifurquer au nord en \(\color{yellow}(2,4)\) ou à l'ouest en \(\color{#6464FF}(3,3)\) puisque \(u_3=c\not=t=v_4\) et que \({\color{yellow}L(2,4)}={\color{#6464FF}L(3,3)}=1\). L'arbre de décision est représenté ci-dessous, un nœud contient les indices \(i\) et \(j\) à gauche et \(L_{i,j}\) à droite et quand \(u_i=v_j\) la branche est étiquettée par le symbole correspondant. Le chemin choisi est en jaune dans la matrice et dans l'arbre de décision et fournit la plsc \(w=ure\). L'arbre montre qu'il en existe une deuxième \(sre\) et que chacune des deux peut être obtenue par trois chemins distincts.

Complexité
Dans la suite nous notons \(n:=|u|\) et \(m:=|v|\). Commençons par l'analyse de l'algorithme Lplsc. L'algorithme construit la matrice \(L\), on peut donc se contenter de compter le nombre d'éléments qui détermine son coût global, il n'y a pas de cas favorable ou défavorable, on a donc une complexité en \(\Theta(nm)\).
Pour rechercher une seule plsc, il faut trouver le chemin le plus court qui part de l'angle sud-est de la matrice \(L\) et qui aboutit à la ligne ou à la colonne \(\varepsilon\), autrement dit le minimum de \(n\) et \(m\) auquel il faut rajouter le coût de la construction de la matrice \(L\) soit
\begin{equation}\label{eq:compit} \Theta(nm) + \Theta(\min\{n,m\}) = \Theta(nm). \end{equation}Si l'on veut calculer \(\Pi(u,v)\) avec l'algorithme récursif il faut remarquer qu'il y a deux appels récursifs à chaque fois que les symboles sont différents et que les deux valeurs au nord et à l'ouest sont égales. On définit alors implicitement un arbre binaire dont la profondeur est majorée par un chemin de longueur maximale entre les angles Sud-Est et Nord-Ouest, soit \(n+m\) ce qui nous donne une complexité exponentielle de \(O(2^{n+m})\) dans le pire des cas.
Travaux pratiques
On obtient la matrice \(L\) suivante :
On en déduit que \(\Lambda(u,v)\) = et que .